Domovská stránka
Matematika
Vlastnosti, vzťahy a vzorce obdĺžnika, príklady

Matematika

Vlastnosti, vzťahy a vzorce obdĺžnika, príklady

A obdĺžnik Je to plochá postava štyroch strán, takže dve z nich sú navzájom rovnobežné, nazývané základne A tiež jedna z ostatných strán je kolmá na základne.

Z tohto dôvodu sú dva vnútorné uhly rovné, to znamená, že merajú 90 °. Preto názov „obdĺžnika“, ktorý je daný obrázku. Tieto vlastnosti objasňuje nasledujúci obrázok obdĺžnika

[TOC]

Prvky lichobežníka

Prvky lichobežníka sú:

-Základne

-Vrcholy

-Výška

-Vnútorné uhly

-Priemerná základňa

-Diagonála

Tieto prvky podrobne opísame pomocou obrázkov 1 a 2:

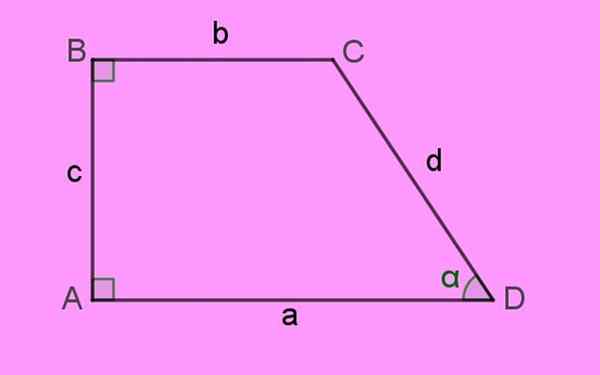
postava 1. Trapeze obdĺžnika, charakterizovaný tým, že má dva vnútorné uhly 90 °: a a b. Zdroj: f. Zapata.

Strany lichobežníka obdĺžnika sú označené malými písmenami A, B, C a D. Rohy obrázku alebo Vrcholy Sú uvedené v kapitálových listoch. Konečne Vnútorné uhly Sú vyjadrené gréckymi písmenami.

Podľa definície základne Z tohto lichobežníka sú strany A a B, ktoré sú pozorované, sú rovnobežné a tiež majú inú dĺžku.

Kolmá strana na obidvoch základoch je strana c vľavo, čo je výška h lichobežník. A nakoniec je tu strana D, ktorá tvorí akútny uhol α so stranou a.

Súčet Vnútorné uhly kvadrilaterálne je 360 °. Ľahko sa oceňuje, že chýbajúci uhol C na obrázku je 180 - α.

Ten priemerná základňa Je to segment, ktorý sa spája so strednými časťami, ktoré nie sú paralelné strany (segment EF na obrázku 2).

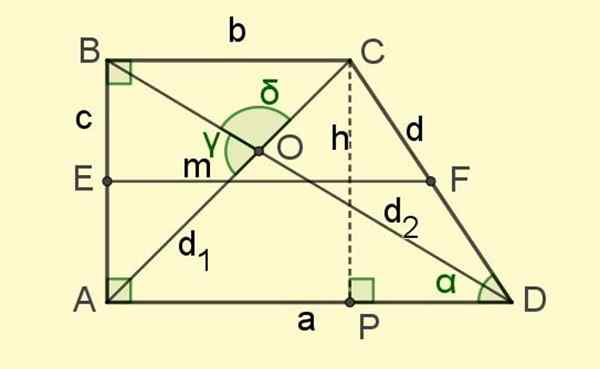Obrázok 2. Prvky lichobežníka obdĺžnika. Zdroj: f. Zapata.

A nakoniec sú tu diagonály D₁ a d₂, Segmenty, ktoré spájajú opačné vrcholy a ktoré sa pretínajú v bode O (pozri obrázok 2).

Vzťahy a vzorce

Výška h z lichobežníka

H = c

Obvod P

Je to miera obrysu a vypočíta sa pridaním strán:

Obvod = A + B + C + D

Strana d Je vyjadrená z hľadiska výšky alebo strany c Prostredníctvom vety Pythagory:

D = √ (a-b)² + c²

Výmena v obvode:

P = a + b + c + √ (a-b)² + c²

Priemerná základňa

Sú to polo -body základov:

Stredná základňa = (a+b)/2

Niekedy sa nachádza priemerná základňa vyjadrená týmto spôsobom:

Stredná základňa = (hlavná základňa + menšia báza) /2

Oblasť

Oblasť A lichobežníka je produktom priemernej základne podľa výšky:

A = (Hlavná základňa + menšia základňa) x výška /2

A = (a+b) c/2

Diagonály, boky a uhly

Na obrázku 2 sa objavuje niekoľko trojuholníkov. Pre tých, ktorí majú pravdu trojuholníky, ich môžu aplikovať veta Pythagoras a tým, ktorí to neurobia, vety kosínu a prsníka.

Môže vám slúžiť: Transcendentné čísla: čo sú, vzorce, príklady, cvičenia

Týmto spôsobom existujú vzťahy medzi stranami a medzi stranami a vnútornými uhlami lichobežníka.

CPA trojuholník

Je to obdĺžnik, jeho nohy sú rovnaké a majú hodnotu B, zatiaľ čo hypotenus je diagonálna D₁, preto:

d₁² = b² + b² = 2B²

Trojuholník

Je to tiež obdĺžnik, nohy sú do a c (alebo tiež do a h) A hypotenus je d₂, tak to:

d₂² = a² + c²= a² + h²

CDA trojuholník

Pretože tento trojuholník nie je obdĺžnik, aplikuje sa kosínová veta alebo tiež prsník.

Podľa Coseno Theorrem:

d₁² = a² + d² - 2AD cos α

CDP trojuholník

Tento trojuholník je obdĺžnik a so svojimi strán sú zostavené trigonometrické dôvody uhla α:

Sin α = H/D

cos α = pd/d

Ale strana PD = A - B, preto:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Máte tiež:

Tg a = sin a / cos a = h / (a-b) → h = Tg a (a-b)

CDB trojuholník

V tomto trojuholníku máme uhol, ktorého vrchol je v C. Nie je označený na obrázku, ale na začiatku vynikal, že má hodnotu 180 - α. Tento trojuholník nie je obdĺžnik, takže sa dá aplikovať kosínová veta alebo veta prsníka.

Teraz sa dá ľahko preukázať, že:

Sen (180 - a) = sin α

cos (180 - a) = - cos α

Uplatňovanie vety Coseno:

d₂² = d² + b²- 2db cos (180 - a) = d² + b²+ 2db cos α

Príklady obdĺžnikov

Trapezios a najmä obdĺžniky sa nachádzajú na mnohých stranách a niekedy nie vždy hmatateľné. Tu máme niekoľko príkladov:

Tracecio ako dizajnérsky prvok

Geometrické postavy oplývajú v architektúre mnohých budov, ako je tento kostol v New Yorku, ktorý vykazuje štruktúru vo forme obdĺžnikového lichobežníka.

Aj lichobežník je častý v návrhu nádob, nádob, čepelí (Nožnica alebo presné), listy a grafický dizajn.

Obrázok 3. Anjel vo vnútri obdĺžnika lichobežníka v kostole v New Yorku. Zdroj: David Goehring cez Flickr.

Generátor s lichobežníkmi

Elektrické signály môžu byť nielen štvorcový, sínusový alebo trojuholníkový. Existujú tiež lichobežné signály, ktoré sú užitočné v mnohých obvodoch. Na obrázku 4 je lichobežníkový signál zložený z dvoch obdĺžnikov. Medzi nimi tvoria jediný lichobežník Isosceles.

Môže vám slúžiť: DETIVORY 8: Čo sú a ľahké vysvetlenie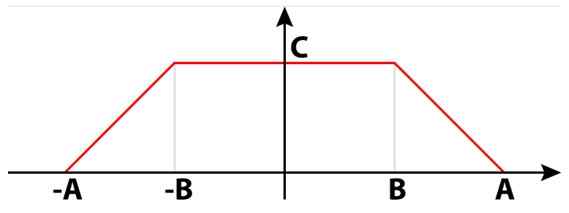

Obrázok 4. Lichobežník. Zdroj: Wikimedia Commons.

V numerickom výpočte

Na výpočet numericky definovaného integrálu funkcie F (x) medzi A a B sa pravidlo lichobežníka používa na priblíženie oblasti pod grafom F (x). Na nasledujúcom obrázku vľavo integrálne prístupy s jedným lichobežníkom obdĺžnika.

Lepším prístupom je prístup správnej postavy s viacerými obdĺžnikmi.

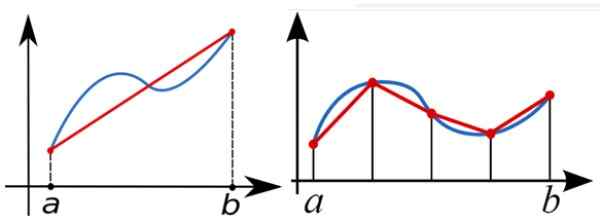Obrázok 5. Definovaný integrál medzi A a B nie je nič iné ako oblasť pod krivkou f (x) medzi týmito hodnotami. Obdĺžnikový lichobežník môže slúžiť ako prvý prístup k tejto oblasti, ale čím viac sa používa lichobežníky, tým lepší prístup. Zdroj: Wikimedia Commons.

Lichobežník

Sily nie sú vždy sústredené na jeden bod, pretože telá, na ktorých konajú, majú značné rozmery. Taký je prípad mosta, cez ktorý vozidlá nepretržite cirkulujú, vodu bazéna na zvislých stenách toho istého alebo strechy, na ktorej sa hromadí voda alebo sneh.

Preto sú sily distribuované na jednotku dĺžky, povrchu alebo objemu, v závislosti od tela, na ktorom pôsobia.

V prípade lúča môže mať sila distribuovaná na jednotku dĺžky rôzne rozdelenie, napríklad súbor obdĺžnikového lichobežníka uvedeného nižšie:

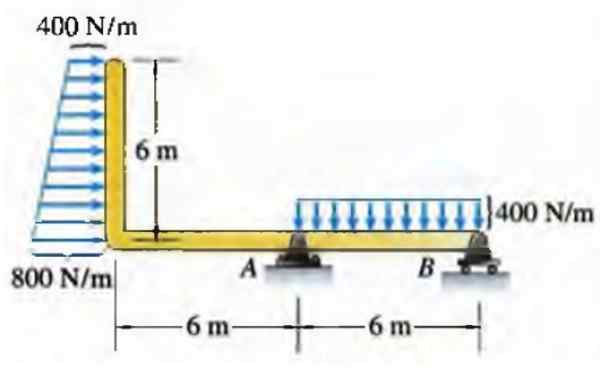Obrázok 6. Zaťaženie lúča. Zdroj: Bedford, do. Devätnásť deväťdesiat šiestich. Statický. Addison Wesley Inter -American.

V skutočnosti nie vždy distribúcie zodpovedajú pravidelným geometrickým formám, ako je tento, ale v mnohých prípadoch to môže byť dobrý prístup.

Ako vzdelávací a vzdelávací nástroj

Bloky a listy s geometrickými tvarmi, vrátane lichobežníkov, sú pre deti veľmi užitočné, aby sa oboznámili od raného veku s fascinujúcim svetom geometrie.

Obrázok 7. Bloky s jednoduchými geometrickými tvarmi. Koľko obdĺžnikov je skrytých v blokoch? Zdroj: Wikimedia Commons.

Vyriešené cvičenia

- Cvičenie 1

V lichobežníku obdĺžnika na obrázku 1 má najväčšia základňa hodnota 50 cm a najmenšia základňa sa rovná 30 cm, je tiež známe, že šikmé bočné meria 35 cm 35 cm. Nájsť:

a) uhol α

b) výška

c) obvod

d) stredná základňa

e) oblasť

f) diagonálne

Roztok

Údaje o príkazoch sú zhrnuté týmto spôsobom:

A = vyššia báza = 50 cm

B = menšia základňa = 30 cm

D = naklonená strana = 35 cm

Môže vám slúžiť: Základné operácie

Ak chcete nájsť uhol α, navštívime časť vzorcov a rovníc, aby sme zistili, ktorý z nich najlepšie vyhovuje ponúkaným údajom. Vyhľadaný uhol sa nachádza v niekoľkých analyzovaných trojuholníkoch, napríklad CDP.

Tam máme tento vzorec, ktorý obsahuje neznáme a tiež údaje, ktoré poznáme:

cos α = (a-b) / d

Preto:

a = oblúky [(a-b) / d] = oblúky [(50-30) / 35] = oblúky 20/35 = 55.15 °

Riešenie B

Z rovnice:

Sin α = H/D

H = D.hriech α = 35 Sen 55.15 ° CM = 28.72 cm

Riešenie c

Obvod je súčet strán a keďže výška sa rovná strane C, musíme:

C = H = 28.72 cm

Preto:

P = (50 + 30 + 35 + 28.72) cm = 143.72 cm

Riešenie d

Priemerná základňa sú semifinále základní:

Stredná báza = (50 + 30 cm)/2 = 40 cm

Riešenie e

Oblasť lichobežníka je:

A = priemerná základňa x výška = 40 cm x 28.72 = 1148.8 cm².

Riešenie f

Pre diagonálne D₁ Tento vzorec je možné použiť:

d₁² = b² + b² = 2B²

d₁²= 2 x (30 cm)² = 1800 cm²

d₁ = √1800 cm² = 42.42 cm

A pre diagonálnu D₂:

d₂² = d² + b²+ 2db cos α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 ° = 3325 cm²

d₂ = √ 3325 cm² = 57.66 cm

Toto nie je jediný spôsob, ako nájsť D₂, Pretože je tu tiež DAB trojuholník.

- Cvičenie 2

Nasledujúci rýchlostný graf v závislosti od mobilu, ktorý má rovnomerne zrýchlený priamy pohyb. Vypočítajte vzdialenosť prejdená mobilom počas časového intervalu medzi 0.5 a 1.2 sekundy.

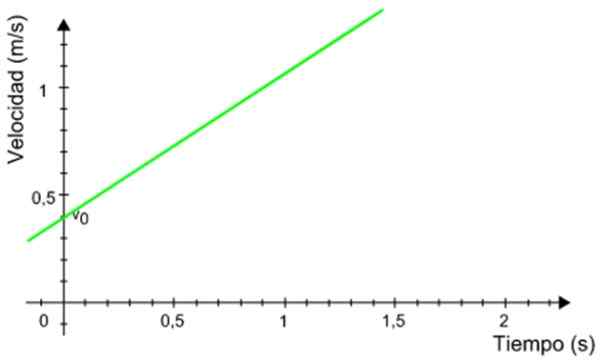Obrázok 8. Grafická proti času mobilu s rovnomerne zrýchleným pohybom reknetu. Zdroj: Wikimedia Commons.

Riešenie

Vzdialenosť prevezená mobilom je rovnocenná s oblasťou pod grafom, vymedzenou uvedeným časovým intervalom.

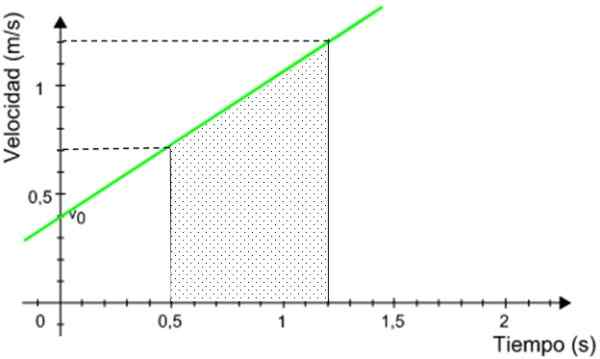Obrázok 9. Vzdialenosť prevezená mobilom je rovnocenná s oblasťou pod grafikou. Zdroj: upravené podľa f. Zapata.

Štiepená oblasť je plocha lichobežníka obdĺžnika, ktorú dal: