Typy integrálov
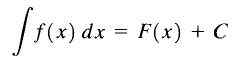
- 3948
- 22
- Mgr. Pravoslav Mokroš
Ten Typy integrálov To, že sme vo výpočte, sú neurčité integrály a definované integrály. Aj keď definované integrály majú oveľa viac aplikácií ako neurčité integrály, je potrebné sa najprv naučiť riešiť neurčité integrály.
Jednou z najatraktívnejších aplikácií definovaných integrálov je výpočet objemu tuhej revolúcie. Oba typy integrálov majú rovnaké vlastnosti linearity a tiež integračné techniky nezávisia od typu integrálu.
Ale napriek tomu, že je veľmi podobný, existuje hlavný rozdiel; V prvom type integrálu je výsledok funkcia (ktorá nie je špecifická), zatiaľ čo v druhom type je výsledok číslo.
Základné typy integrálov
Svet integrálov je veľmi široký, ale v rámci toho môžeme rozlíšiť dva základné typy integrálov, ktoré majú v každodennom živote veľkú uplatniteľnosť.
1- Neurčité integrály
Ak f '(x) = f (x) pre všetky x v doméne F, hovoríme, že F (x) je antidevatívny, primitívny alebo integrál f (x).
Na druhej strane si všimnite, že (f (x)+c) '= f' (x) = f (x), čo naznačuje, že integrál funkcie nie je jedinečný, pretože dáva rôzne hodnoty konštante C Získame rôzne antiderivaty.
Z tohto dôvodu sa F (x)+c nazýva neurčitý integrál F (x) a C sa nazýva konštantná integrácia a píšeme ju takto:
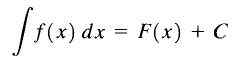 Neurčitý integrál
Neurčitý integrál Ako vidíme, neurčitý integrál funkcie F (x) je rodinou funkcií.
Napríklad, ak chcete vypočítať neurčitú integrál funkcie f (x) = 3x², najprv sa musí nachádzať antiderivat f (x).
Môže vám slúžiť: trinomialJe ľahké poznamenať, že f (x) = x³ je antidevatívny, pretože f '(x) = 3x² je. Preto je možné dospieť k záveru
∫f (x) dx = ∫3x²dx = x³+c.
2- definované integrály
Nech y = f (x) Skutočná funkcia pokračuje v uzavretom intervale [a, b] a je f (x) antidevutívnym f (x). Nazýva sa definovaný integrál f (x) medzi limitmi A a B na číslo f (b) -f (a) a označuje nasledovne:
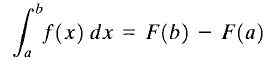 Veta základnej výpočtu
Veta základnej výpočtu Vyššie uvedený vzorec je známy ako „základná veta výpočtu“. Tu sa nazýva dolný limit a „B“ sa nazýva horná hranica. Ako je vidieť, definitívny integrál funkcie je číslo.
V tomto prípade, ak sa v intervale vypočíta definovaný integrál F (x) = 3x² [0,3], získa sa číslo.
Aby sme určili toto číslo, vyberieme f (x) = x³ ako antidevatívne f (x) = 3x². Potom vypočítame f (3) -f (0), ktorý nás vyvoláva v dôsledku 27-0 = 27. Záverom možno povedať, že definovaný integrál F (x) v intervale [0,3] je 27.
Dá sa poznamenať, že ak je zvolený g (x) = x³+3, potom g (x), je antidevatívnym f (x) odlišným od f (x), ale to nemá vplyv na výsledok ako g (3) -G (0) = (27+3)-(3) = 27. Z tohto dôvodu sa v definovaných integráloch neobjaví integračná konštanta.
Jednou z najužitočnejších aplikácií, ktoré má tento typ integrálu, je to, že umožňuje vypočítať plochu (objem) plochej postavy (solídna revolúcia), čím sa stanoví primerané integračné funkcie a limity (a os rotácie).
Medzi definovanými integrálmi nájdeme rôzne rozšírenia tohto, ako sú integrálne línie, povrchové integrály, nesprávne integrály, viacnásobné integrály, okrem iného s veľmi užitočnými aplikáciami vo vede a inžinierstve.
Môže vám slúžiť: rozdiel medzi kruhom a obvodom (s príkladmi)Odkazy
- Kishan, h. (2005). Integrálny počet. Vydavatelia a distribútori Atlantiku.
- Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia (Deviate vydanie.). Sála.

