Tretí zákon termodynamiky, rovnice, príklady

Ten Tretí zákon termodynamiky uvádza, že entropia uzavretého termodynamického systému v rovnováhe má tendenciu byť minimálna a konštantná, pretože jej teplota sa blíži 0 kelvin.

Táto hodnota entropie bude nezávislá od systémových premenných (tlak alebo aplikované magnetické pole). Čo sa stane, je to, že keďže teplota je bližšie k 0 K, procesy v systéme sa zastavia a ako je entropia mierou vnútorného agitácie, nevyhnutne zostupuje.

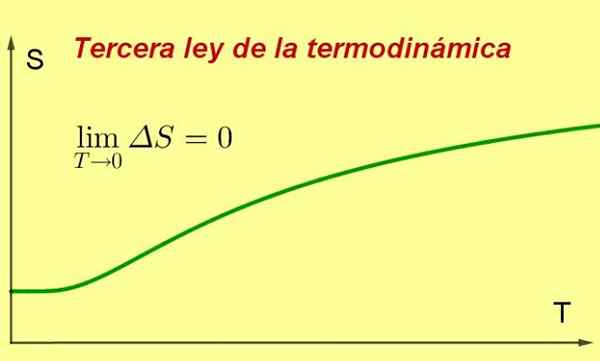
postava 1. Keď sa teplota systému blíži k absolútnej nule, jej entropia dosahuje minimálnu a konštantnú hodnotu. Zdroj: Pripravený F. Zapata ..

[TOC]

Predchádzajúce koncepty

Na pochopenie rozsahu tretieho zákona termodynamiky, ktoré je relevantné pre veľmi nízke teploty, je potrebné preskúmať tieto koncepty:

Termodynamický systém

Zvyčajne sa týka plynu, kvapaliny alebo tuhej látky. Čo nie je súčasťou systému, sa nazýva okolo. Najbežnejším termodynamickým systémom je ideálny plyn, ktorý pozostáva z n častíc (atómov), ktoré interagujú iba prostredníctvom elastických kolízií.

Izolované, zatvorené alebo otvorené systémy

Izolované systémy nie sú povolené výmenou s prostredím. Uzavreté systémy si nevymieňajú záležitosť s životným prostredím, ale horúčava. Nakoniec si môžu otvorené systémy vymeniť hmotu a zahrievanie životného prostredia.

Makro -state a mikrostat

MakroState systému je sada hodnôt, ktoré majú jeho premenné: tlak, teplota, objem, počet krtkov, entropia a vnútorná energia. Na druhej strane, mikroestum -v prípade ideálneho plynu -je daná polohou a hybnosťou každého z častíc n, ktoré ju v určitom okamihu tvoria, v určitom okamihu. 

Mnoho mikrotátov môže viesť k rovnakému makro -state. V plyne pri teplote miestnosti je počet možných mikrostatu obrovský, pretože počet častíc, ktoré ho tvoria, rôzne polohy a rôzne energie, ktoré môžu prijať. 

Vzorce a rovnice

Entropia, ako sme povedali, je termodynamická makroskopická premenná, ktorá meria systém molekulárnej poruchy systému. Stupeň poruchy systému je väčší v rozsahu, v akom je počet možných mikrostatov väčší. 

Tento koncept je potrebný na formulovanie tretieho zákona termodynamiky v matematickej podobe. Či už ide o entropiu systému, potom:

To znamená, že entropia v uzavretom systéme sa nemení, keď jej teplota t má tendenciu k absolútnej nule.

Entropia je premenná makroskopického stavu, ktorá priamo súvisí s počtom možných mikrostatu systému pomocou nasledujúceho vzorca:

S = k ln (w)

V predchádzajúcej rovnici: Siež predstavuje entropiu, W počet možných mikrostatov systému a klimatizovať Je to Boltzmannova konštanta (K = 1.38 x 10^-23 J/k). To znamená, že entropia systému je klimatizovať krát prírodný logaritmus počtu možných mikrostav.

Výpočet absolútnej entropie látky

Je možné definovať absolútnu entropiu čistej látky na základe definície variácie entropie:

Kde ΔQ je nekonečná variácia tepla a T je teplota. Táto rovnica je platná, ak je proces reverzibilný (Rev).Ak ide o proces izobarického - konštantného tlaku, je možné napísať takúto variáciu teploty nekonečnej teploty:

Δq = n . c_p .Dt

Tu je CP špecifické molárne teplo a N Počet mólov. Molárna špecifická závislosť tepla s teplotou je experimentálne získaná skutočnosť a je známa mnohými čistými látkami.

Môže vám slúžiť: Solárny systém: planéty, charakteristiky, pôvod, vývoj

Podľa tretieho zákona v čistých látkach: 

Takže absolútna entropia mol čistej látky, ako napríklad:

V predchádzajúcej zápise lišta naznačuje, že ide o entropiu mólu látky a superson ° označuje čistú látku.

Žiadosti

V každodennom živote má tretí zákon termodynamiky málo aplikácií, celkom v rozpore s prvým a druhým zákonom. Je to preto, že je to princíp, ktorý sa týka toho, čo sa deje v systéme, keď sa blíži k absolútnemu 0, hodnosti zriedkavých teplôt.

V skutočnosti dosiahnite absolútne alebo -273,15 ° C je nemožné (pozri príklad 1 neskôr) sa však pri štúdiu odozvy materiálov pri veľmi nízkych teplotách uplatňuje tretí zákon. 

Vďaka tomu sa objavili dôležité pokroky v kondenzovanej záležitosti, napríklad:

-Superfluidia (pozri príklad 2 neskôr)

-Supravodivosť 

-Laserové techniky chladenia 

-Kondenzát Bose-Einstein 

-Fermi nadbytočné plyny.

Obrázok 2. Nadbytočné tekuté hélium. Zdroj: Wikimedia Commons.

Pri extrémne nízkych teplotách umožňuje zostup entropie vznik zaujímavých kvantových javov. Preto sa pozrime, čo sa stane s entropiou systému s veľmi nízkou teplotou.

Entropia systému s nízkou teplotou

Ak máte perfektnú kryštalickú látku, jej minimálna entropia je presne nula, pretože je veľmi uprataná. Pri teplotách blízko absolútneho 0 je hmota v kondenzovanom stave (kvapalina alebo tuhá látka) a vibrácie skla sú minimálne.

Niektorí autori považujú alternatívne vyhlásenie tretieho zákona o termodynamike nasledujúce:

„Ak záležitosť kondenzuje dokonalý kryštál, keď teplota má sklon k absolútnej nule, entropia má tendenciu presne k nule“. 

Presudvíme niektoré aspekty predchádzajúceho vyhlásenia: 

- Perfect Crystal je ten, v ktorom je každá molekula identická a v ktorej sa molekulárna štruktúra opakuje identicky ako celok.

- Keďže teplota má tendenciu k absolútnej nule, atómové vibrácie takmer úplne znižujú.

Potom sklo tvorí jednu možnú konfiguráciu alebo mikrostatementovanie, to znamená W = 1, A preto sa entropia rovná nule:

 S = k ln (1) = 0

Ale nie tak dlho, ako sa materiál ochladzuje blízko absolútnej nuly, tvorí kryštál, oveľa menej je tento kryštál dokonalý. K tomu dochádza iba vtedy, ak je proces chladenia veľmi pomalý a reverzibilný.

V opačnom prípade by faktory, ako sú nečistoty prítomné v skle. Preto w> 1 a entropia by bola väčšia ako 0.

Zvyšková entropia

Ak je proces chladenia náhly, v rovnakom systéme prechádza sledom nebavolných stavov, čo vedie k ukážke materiálu. V tomto prípade neexistuje žiadna kryštalická a usporiadaná štruktúra, ale amorfná tuhá látka, ktorej štruktúra je podobná štruktúre kvapaliny. 

V takom prípade nie je minimálna hodnota entropie v blízkosti absolútneho nuly nula, pretože počet mikrostatov je oveľa väčší ako 1. Rozdiel medzi touto entropiou a nulovou entropiou perfektného kryštalického stavu je známy ako zvyšková entropia.

Vysvetlenie je, že pod určitou prahovou teplotou nemá systém žiadnu inú možnosť ako Occy.

Môže vám slúžiť: Prvý zákon termodynamiky: vzorce, rovnice, príklady

Budú zodpovední za udržiavanie konštantnej entropie, aj keď teplota zostupuje smerom k absolútnej nule.

Príklady

Príklad 1: Absolútna nula a neurčenie Heisenbergu

Princíp neurčitosti v Heisenbergu ustanovuje, že neistota v polohe a hybnosť častíc, napríklad v atómoch kryštalickej siete, nie sú nezávislé od ostatných, ale sledujú nasledujúcu nerovnosť:

Δx ⋅ δp ≥ h

Kde H je Planckova konštanta. To znamená, že neistota v polohe vynásobená neistotou v hybnosti (hmotnosť na rýchlosť) je väčšia alebo rovná Planckovej konštante, ktorej hodnota je veľmi malá, ale nie nula: H = 6.63 x 10-3. 4 J · s.

A čo má zásada neistoty spoločné s tretím zákonom o termodynamike? Ak je poloha atómov kryštalickej siete pevná a presná (presná (Δx = 0) Potom rýchlosť týchto atómov môže mať akúkoľvek hodnotu medzi 0 a nekonečnosťou. Je to v rozpore skutočnosťou, že v absolútnom nule každý pohyb tepelnej agitácie prestane.

Recipročne, ak to začneme s absolútnou nulou teploty, všetky agitácie prestanú a hybnosť každého atómu siete je presne nula (Δp = 0), potom by princíp neistoty Heisenbergu naznačoval, že neurčitosť v pozíciách každého atómu by bola nekonečná, to znamená, že môžu byť v akejkoľvek pozícii. 

V dôsledku predchádzajúceho vyhlásenia by počet mikrostatov mal tendenciu mať nekonečno a entropia by tiež mala neurčitú hodnotu. 

Príklad 2: Superfluidia a podivný prípad hélia-4

V nadpriemernosti, ktorá sa vyskytuje pri veľmi nízkych teplotách, hmota stráca vnútorné trenie medzi molekulami, ktoré sa nazývajú hrebeň. V tomto prípade by tekutina mohla navždy cirkulovať bez trenia, ale problém je pri týchto teplotách takmer nič nie je tekutý okrem hélia.

Hélium a hélium 4 (jeho najhojnejší izotop) predstavuje jedinečný prípad, pretože pri atmosférickom tlaku a teplotách blízko absolútneho nuly zostáva hélium kvapalné. 

Keď sa hélium-4 predkladá pri teplote pod 2.2 K pri atmosférickom tlaku sa stáva a nadbytočný. Tento objav sa vyskytol v roku 1911 v Leydene holandským fyzikom Heikom Kamerlinghom Onnesom (1853-1926).

Obrázok 3. Holandský fyzik Heike Kamerlingh Onnes (1853-1926). Zdroj: Wikimedia Commons.

Helio-4 Atom je a Bosón. Bozóny, na rozdiel od fermónov, sú častice, ktoré môžu zaberať všetok rovnaký kvantový stav. Preto Bosons nespĺňajú Pauliho princíp vylúčenia.

Potom všetky atómy hélium-4 pri teplotách pod 2.2 K zaberá rovnaký kvantový stav, a preto nie je nič viac ako jeden možný mikrostat, čo naznačuje, že nadbytočný hélium-4 má S = 0.

Vyriešené cvičenia

- Cvičenie 1

Zvážte jednoduchý prípad pozostávajúci zo systému vytvoreného iba tromi časticami, ktoré majú tri hladiny energie. Pre tento jednoduchý systém:

a) Určite počet mikrostatu pre tri teplotné rozsahy:

-vysoký 

-Polovica 

-Nízky

b) Stanovte entropiu Boltzmannovej rovnice v rôznych teplotných rozsahoch. 

c) Diskutujte o výsledkoch a vysvetlite, či je alebo nie sú v rozpore s tretím zákonom o termodynamike.

Roztok

Na molekulárnej a atómovej stupnici sa kvantifikujú energie, ktoré môže systém prijať, čo znamená, že môžu trvať iba určité diskrétne hodnoty. Okrem toho, keď sú teploty také nízke, častice, ktoré tvoria systém. 

Môže vám slúžiť: magnetická indukcia: vzorce, ako sa vypočítajú a príklady

Vysoká teplota

Ak má systém relatívne vysokú teplotu, potom majú častice dostatok energie na obsadenie akýchkoľvek dostupných úrovní, čo vedie k 10 možným mikrostatom, ktoré sa objavia na nasledujúcom obrázku:

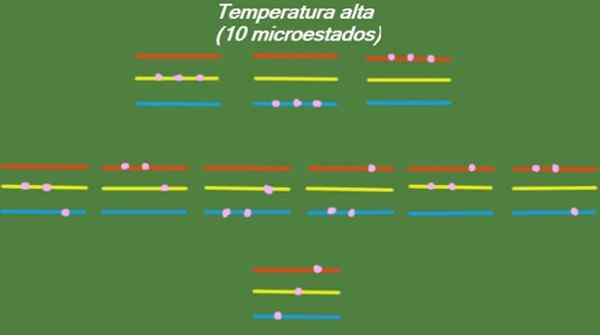Obrázok 4. Možné stavy pri vysokej teplote za rok vyriešené 1. Zdroj: Pripravený F. Zapata.

Stredná teplota

V prípade, že systém má strednú teplotu, potom častice, ktoré ju tvoria, nemajú dostatok energie na zaberanie najvyššej úrovne energie. Možné mikrostaty sú znázornené na obrázku:

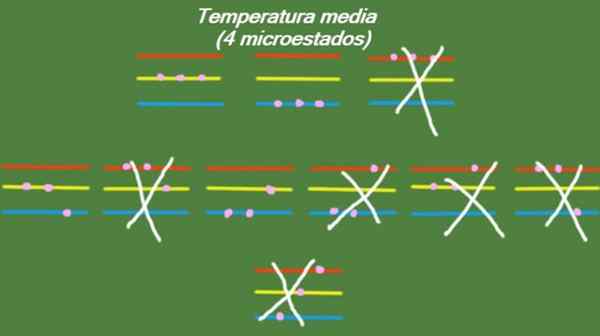Obrázok 5. Mikro -state pri priemernej teplote pre vyriešený cvičebný systém 1. Zdroj: Pripravený F. Zapata.

Nízka teplota

Ak teplota naďalej zostupuje v našich idealizovaných troch častiach a troch úrovniach energie, potom budú mať častice takú malú energiu, že môžu zaberať iba najnižšiu úroveň. V tomto prípade existuje iba 1 možný mikrostat, ako je zrejmé na obrázku 6:

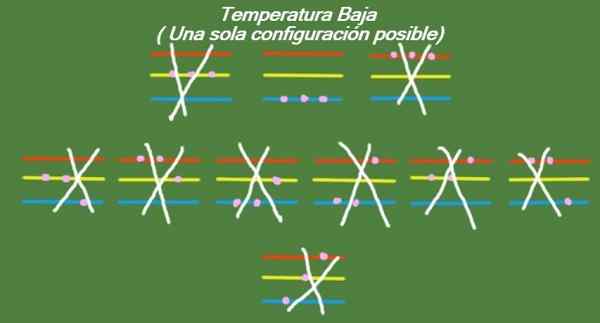Obrázok 6. Pri nízkej teplote je možná konfigurácia (vlastné rozpracovanie)

Riešenie B

Už známe počet mikrostatov v každom teplotnom rozsahu, už môžeme použiť Boltzmannovu rovnicu uvedenú predtým na nájdenie entropie v každom prípade.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J/k (Vysoká teplota)

S = k ln (4) = 1.38 x k = 1.92 x 10-23 J/k (Stredná teplota)

A nakoniec:

S = k ln (1) = 0 (Nízka teplota)

Riešenie c

V prvom rade si všimneme, že entropia klesá, keď teplota klesá, podľa očakávania. Ale pre najnižšie hodnoty teploty sa dosiahne prahová hodnota, z ktorej sa dosiahne základný stav systému.

Aj keď je teplota čo najbližšie k absolútnej nule, nie sú k dispozícii žiadne menšie stavy. Potom entropia udržiava svoju konštantnú minimálnu hodnotu, ktorá v našom príklade je s = 0.

Toto cvičenie ilustruje na úrovni mikrotátov systému, dôvod, prečo sa splní tretí zákon termodynamiky.

- Cvičenie 2

Dôvod Ak je ďalšie vyhlásenie pravdivé alebo nepravdivé:

„Entropia systému pri absolútnej nulovej teplote je presne nula“.

Odôvodnite odpoveď a opíšte niektoré príklady.

Riešenie

Odpoveď znie: false.

Najprv sa nedá dosiahnuť absolútna teplota, pretože princíp neistoty Heisenberga a tretí termodynamika by sa porušili. 

Je veľmi dôležité poznamenať, že v treťom zákone sa nehovorí, čo sa deje v absolútnom 0, ale keď je teplota nekonečne blízko absolútneho 0. Rozdiel je jemný, ale významný.

Tretí zákon nepotvrdzuje, že keď teplota má svojvoľne hodnotu blízko k absolútnej nule, entropia má tendenciu nula nulu. Stalo by sa to iba v predtým analyzovanom prípade: Perfect Crystal, ktorý je idealizáciou.

Mnoho systémov mikroskopických mierok, to znamená, že v kvantovej mierke majú svoju úroveň energetickej základne degenerovaný, Čo znamená existenciu niekoľkých konfigurácií na najnižšej úrovni energie. 

Vyššie uvedené znamená, že v týchto systémoch by entropia nikdy nebola presne nula. Ani by entropia bola presne nula v systémoch, ktoré sú vitrifikované, keď má teplota tendenciu k absolútnej nule. V tomto prípade zvyšková entropia Pred videným.

Je to preto, že ich molekuly boli „uviaznuté“ skôr, ako zaberajú najnižšiu dostupnú úroveň energie, čo výrazne zvyšuje počet možných mikrostatu, čo znemožňuje, aby entropia bola presne nula nula.

Odkazy

1. Cengel a. 2012. Termodynamika. 7. vydanie. McGraw Hill. 347.
2. Laboratórium pohonu prúdu. Najchladnejšie miesto vo vesmíre. Získané z: ColdatomLab.Jpl.hrniec.Vláda.
3. González, a. Entropia a spontánnosť. Získané z: Geocities.WS
4. Kupovať. Čo je praktické používanie tretieho zákona termodynamiky?. Získané z: Quora.com
5. Všeobecná chémia. Tretí princíp termodynamiky. Získané z: Korint.Pucp.Edu.pešo
6. Tretí zákon termodynamiky. Obnovené z: YouTube.com
7. Wikipedia. Entropický zvyšok. Zdroj: In.Wikipedia.com
8. Wikipedia. Tretí zákon termodynamiky. Zdroj: In.Wikipedia.com