Binomická veta

Čo je binomická veta?

On binomická veta Je to rovnica, ktorá nám hovorí, ako sa vyvíja vyjadrenie formulára (a+b)ⁿ Pre nejaké prirodzené číslo n. Binomén nie je ničím iným ako súčtom dvoch prvkov, ako napríklad (a+b). Umožňuje nám tiež poznať termín, ktorý dal^{klimatizovať}b^N-k Aký je koeficient, ktorý ho sprevádza.

Táto veta sa bežne pripisuje anglickému vynálezcovi, fyzickému a matematikemu Sir Isaacovi Newtonovi; Zistili sa však rôzne záznamy, ktoré naznačujú, že jej existencia už bola známa na Blízkom východe, okolo roku 1000.

Kombinácia

Binomická veta ma matematicky hovorí:

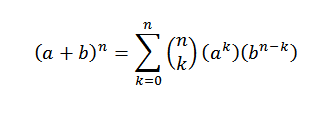
V tomto výraze A a B sú reálne čísla a n je prirodzené číslo.

Pred predložením demonštrácie pozrime sa na niektoré potrebné základné koncepty, ktoré sú potrebné.

Kombinátorové číslo alebo kombinácie n v K sú vyjadrené takto:

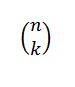
To vyjadruje hodnotu toho, koľko podmnožiny s prvkami K je možné zvoliť zo súboru n prvkov. Jeho algebraický výraz je daný:

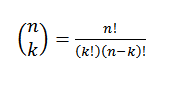
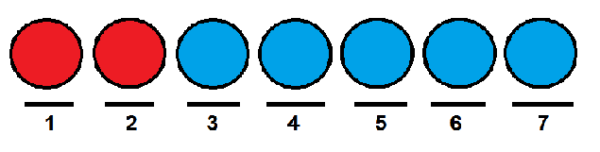
Pozrime sa na príklad: Predpokladajme, že máme skupinu siedmich loptičiek, z ktorých dve sú červené a zvyšok sú modré.

Chceme vedieť, koľko spôsobov si ich môžeme objednať v rade. Jedným zo spôsobov by mohlo byť umiestnenie dvoch červených do prvej a druhej polohy a zvyšok loptičiek v pozíciách, ktoré zostávajú.

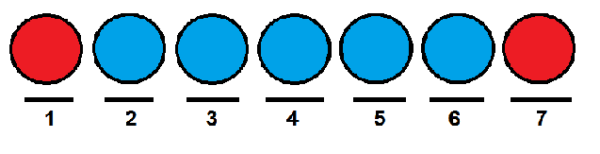
Podobne ako v predchádzajúcom prípade by sme mohli dať červeným loptičkám prvú a poslednú pozíciu a zaberať ostatných modrými loptičkami.

Teraz je efektívny spôsob, ako spočítať, koľko spôsobov si môžeme objednať lopty v rade, používa kombinatorické čísla. Každú pozíciu vidíme ako prvok nasledujúcej sady:

Môže vám slúžiť: perfektné čísla: Ako ich identifikovať a príklady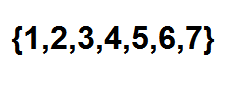

Nižšie je len na výber podmnožiny dvoch prvkov, v ktorých každý z týchto prvkov predstavuje polohu, ktorú budú červené gule zaberať. Túto voľbu môžeme urobiť podľa vzťahu, ktorý dal:

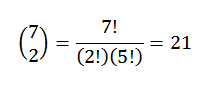
Týmto spôsobom máme, že existuje 21 spôsobov, ako si takéto lopty objednať.

Všeobecná myšlienka tohto príkladu bude veľmi užitočná pri demonštrácii binomickej vety. Pozrime sa na konkrétny prípad: Ak n = 4, máme (a+b)⁴, To nie je nič viac ako:

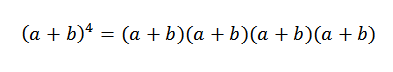
Keď vyvíjame tento produkt, máme súčet výrazov získaných vynásobením prvku každého zo štyroch faktorov (a+b). Budeme teda mať výrazy, ktoré budú vo forme:

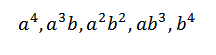
Keby sme chceli získať termín formulára⁴, Stačí len vynásobiť nasledovne:

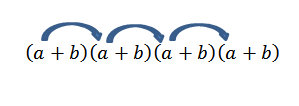
Všimnite si, že existuje iba jeden spôsob, ako získať tento prvok; Čo sa však stane, ak teraz hľadáme koniec formulára²b²? Keďže „A“ a „B“ sú skutočné čísla, a preto stojí za to komutatívne právo, musíme získať tento výraz, aby sme sa množili s členmi, ako to naznačuje šípky.

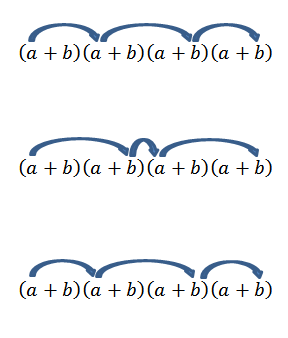
Vykonanie všetkých týchto operácií je zvyčajne trochu únavné, ale ak vidíme termín „A“ ako kombináciu, v ktorej chceme vedieť, koľko spôsobov si môžeme zvoliť dva „A“ zo súboru štyroch faktorov, môžeme použiť myšlienku Predchádzajúci príklad predchádzajúceho príkladu. Takže máme nasledujúce:

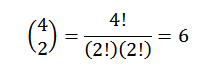
Vieme teda, že v konečnom vývoji expresie (a+b)⁴ Budeme mať presne 6²b². Pomocou rovnakej myšlienky pre iné prvky musíte:

Môže vám slúžiť: Transcendentné čísla: čo sú, vzorce, príklady, cvičenia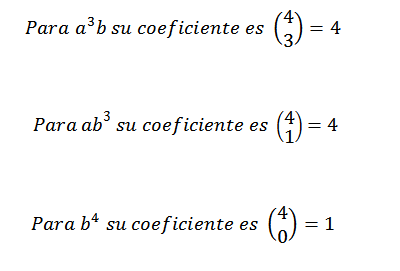

Potom pridáme vyššie uvedené výrazy a musíme:

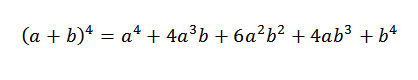
Je to formálna demonštrácia pre všeobecný prípad, v ktorom je „n“ akékoľvek prirodzené číslo.

Demonštrácia

Všimnite si, že pojmy zostané pri vývoji (a+b)ⁿ Sú z formulára do^{klimatizovať}b^N-k, kde k = 0,1,…, n. Pomocou myšlienky predchádzajúceho príkladu máme spôsob, ako zvoliť premenné „K“ a “z faktorov„ N “je:

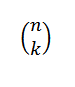
Pri výbere týmto spôsobom automaticky vyberáme premenné N-K „B“. Nasleduje to:

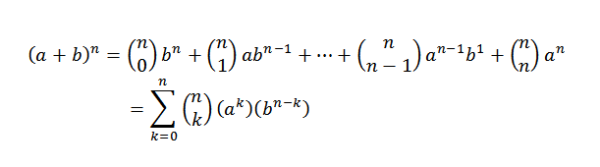
Príklady

Vzhľadom na (a+b)⁵, Aký by bol váš vývoj?

Pre binomickú vetu musíme:

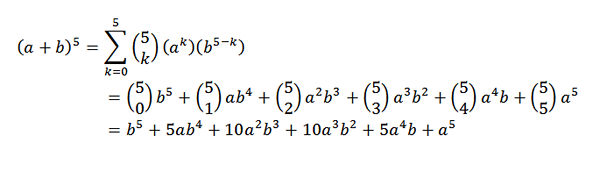
Binomická veta je veľmi užitočná, ak máme výraz, v ktorom chceme vedieť, aký je koeficient konkrétneho pojmu bez toho, aby sme museli vykonať úplný vývoj. Ako príklad môžeme vziať nasledujúce neznáme: Čo je koeficient X⁷a⁹ Vo vývoji (x + y)¹⁶?

Pre binomickú vetu máme, že koeficient je:

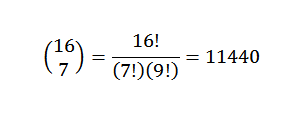
Ďalším príkladom by bolo: čo je koeficient X⁵a⁸ Vo vývoji (3x-7y)¹³?

Najprv prepíšeme výraz pohodlne; toto je:

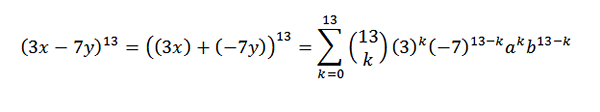
Potom, pomocou binomickej vety, máme, že vyhľadávaný koeficient je, keď máte k = 5

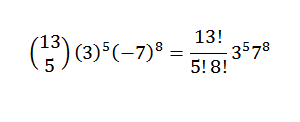
Ďalším príkladom použitia tejto vety je demonštrácia niektorých spoločných identít, ako sú tie, ktoré spomenme nižšie.

Identita 1

Ak je „n“ prirodzené číslo, musíme:

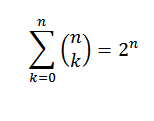
Na demonštráciu používame binomickú vetu, kde „A“ aj „B“ majú hodnotu 1. Potom máme:

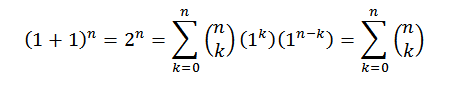
Týmto spôsobom sme dokázali prvú identitu.

Môže vám slúžiť: náhodné výbery s výmenou alebo bez výmeny

Identita 2

Ak je „n“ prirodzené číslo, potom

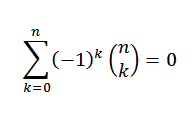
Pre binomickú vetu musíme:

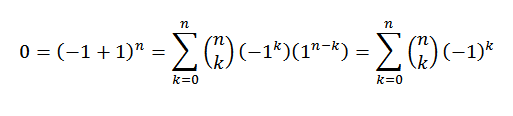
Ďalšia demonštrácia

Môžeme urobiť inú demonštráciu pre binomickú vetu pomocou indukčnej metódy a identity Pascala, ktorá nám hovorí, že ak „n“ a „k“ sú pozitívne celé čísla, ktoré sa stretávajú s n ≥ k, potom:

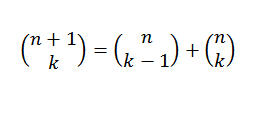
Indukčná demonštrácia

Pozrime sa, že induktívna základňa je splnená.  Ak n = 1, musíme:

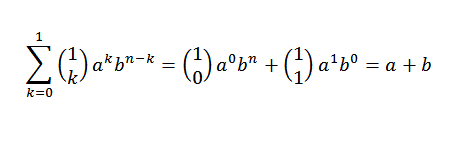
Skutočne vidíme, že je splnený. Teraz, buď n = j tak, že je splnené:

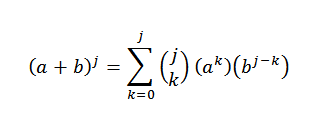
Chceme vidieť, že pre n = j+1 je pravda, že:

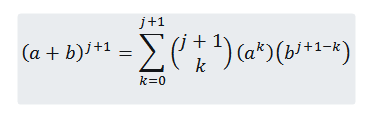
Takže musíme:

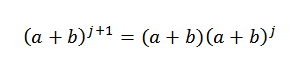
Hypotézou vieme, že:

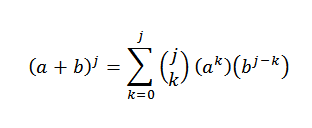
Potom pomocou distribučnej vlastnosti:

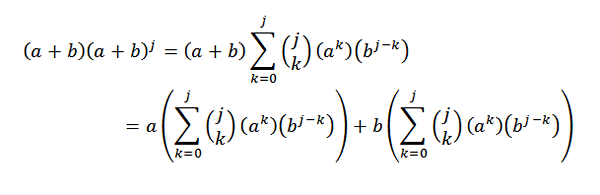
Následne vývoj každého zo zhrnutí je:

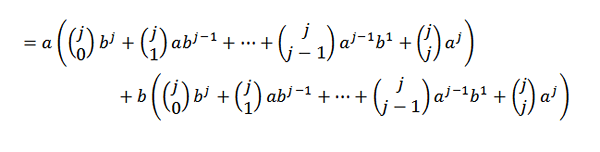
Teraz, ak sme sa pohodlne zoskupili, musíme:

Pomocou Pascalovej identity musíme:

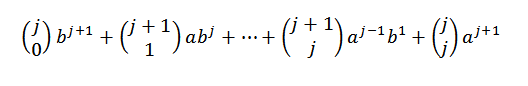
Nakoniec si všimnite, že:

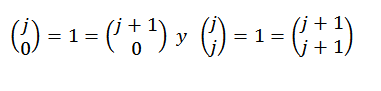
Preto vidíme, že binomická veta je splnená pre každé „n“ patriace k prírodným číslom, a tým sa test končí.

Zvedavosť

Kombinátorové číslo (NK) sa tiež nazýva binomický koeficient, pretože je to presne koeficient, ktorý sa objavuje pri vývoji binomiálneho binomiálneho (a+b)ⁿ.

Isaac Newton dal zovšeobecnenie tejto vety pre prípad, v ktorom je exponent skutočným číslom; Táto veta je známa ako Newtonova binomická veta.

Už v staroveku bol tento výsledok známy pre konkrétny prípad, keď n = 2. Tento prípad je uvedený v Predmety euklid.