Torricelliova veta

Čo je Torricelliho veta?

On Torricelliova veta o princíp Torricelli uvádza, že rýchlosť kvapaliny, ktorá vyjde cez otvor v stene nádrže alebo nádob Diera.

Veta je znázornená na nasledujúcom obrázku:

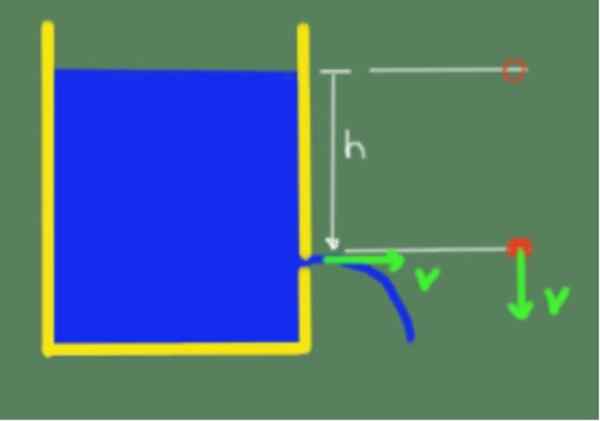Ilustrácia Torricelliho vety. Zdroj: Self Made.

Kvôli Torricelliho vete potom môžeme povedať, že rýchlosť výstupu kvapaliny otvorom, ktorá je až do výšky h pod voľným povrchom kvapaliny, je daná nasledujúcim vzorcom:

Kde g je zrýchlenie gravitácie a H je výška od otvoru po voľný povrch kvapaliny.

Evanjelista Torricelli bol postavou a matematik narodený v meste Faenza v Taliansku v roku 1608. Torricelli sa pripisuje vynálezu barometra ortuti a uznáva sa tlaková jednotka nazývaná „Torr“, ktorá je ekvivalentná milimetra ortuti (mm Hg).

Demonštrácia vety

V Torricelliho vete a vo vzorci, ktorý dáva rýchlosť, predpokladá, že straty v dôsledku viskozity sú opovrhnutiahodné, pretože vo voľnom páde sa predpokladá, že trenie v dôsledku vzduchu, ktorý obklopuje objekt, ktorý padá.

Predchádzajúci predpoklad je vo väčšine prípadov primeraný a tiež naznačuje zachovanie mechanickej energie.

Aby sme demonštrovali vetu, v prvom rade nájdeme vzorec rýchlosti pre objekt, ktorý sa uvoľňuje s nulovou počiatočnou rýchlosťou, z rovnakej výšky ako povrch kvapaliny v nádrži.

Môže vám slúžiť: tri rozmerové vlny: Koncept, typy a príklady

Princíp zachovania energie sa použije na získanie rýchlosti objektu, ktorý spadne, keď výška klesla h rovná sa od diery od diery po voľný povrch.

Keďže neexistujú žiadne straty trenia, je platné uplatňovať zásadu mechanickej ochrany energie. Predpokladajme, že objekt, ktorý padá.

Objekt, ktorý padá

Keď sa objekt uvoľňuje z výšky rovnajúcej sa výške voľného povrchu kvapaliny, jej energia je iba gravitačný potenciál, pretože jeho rýchlosť je nula, a preto jej kinetická energia je nula. Potenciálne EP EP je dané:

EP = m g h

Keď ide pred otvor, jeho výška je nula, potom je potenciálna energia nula, takže má iba kinetickú energiu EC daná:

EC = ½ m v²

Pretože energia je zachovaná EP = EC toho, čo sa získa:

½ m v² = m g h

Vymazanie rýchlosti vložka Potom sa získa vzor Torricelli:

Tekutina, ktorá vychádza z diery

Ďalej nájdeme rýchlosť výstupu kvapaliny cez otvor, aby sme preukázali, že sa zhoduje s rýchlosťou, ktorá bola práve vypočítaná pre objekt, ktorý voľne padá.

Z tohto.

Bernoulliho princíp je formulovaný takto:

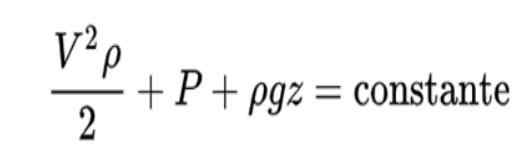
Interpretácia tohto vzorca je nasledovná:

• Prvý termín predstavuje kinetickú energiu tekutiny na jednotku objemu
• Druhá predstavuje prácu vykonanú tlakom na jednotku priečnej oblasti
• Tretia predstavuje energiu gravitačného potenciálu na jednotku objemu tekutiny.

Môže vám slúžiť: Okamžitá rýchlosť: definícia, vzorec, výpočet a cvičenia

Keď začíname z predpokladu, ktorá je ideálnou tekutinou, v netburantných podmienkach s relatívne nízkymi rýchlosťami, potom je potrebné potvrdiť, že mechanická energia na jednotku objemu v tekutine je konštantná vo všetkých oblastiach alebo priečnych častiach rovnakých.

V tomto vzorci Vložka je rýchlosť tekutiny, ρ Hustota tekutín, P tlak a z Vertikálna poloha.

Na obrázku, ktorý je uvedený nižšie, Torricelliho vzorec je demonštrovaný na základe princípu Bernoulli.

Aplikujeme Bernoulliho vzorec na voľný povrch kvapaliny, ktorú označujeme za (1) a vo výstupnom diere, ktorý označujeme (2). Hladina nulovej výšky bola vybraná s výstupným otvorom.

Pod predpokladom, že prierez v bode (1) je oveľa väčší ako v (2), potom môžeme predpokladať, že rýchlosť zníženia kvapaliny v (1) je prakticky nedbanlivosť.

Preto bol umiestnený V₁= 0, tlak, na ktorý je kvapalina vystavená (1), je atmosférický tlak a výška meraná z otvoru je h.

Pre výstupnú časť (2) Predpokladáme, že výstupná rýchlosť je V, tlak, na ktorý je tiež vystavená kvapalina do výstupu, je atmosférický tlak a výška výstupu je nula.

Hodnoty zodpovedajúce sekciám (1) a (2) sú nahradené vo vzorci Bernoulli a rovné. Rovnosť je platná, pretože predpokladáme, že tekutina je ideálna a neexistujú žiadne viskózne straty trenia. Akonáhle sa všetky výrazy zjednodušia, rýchlosť sa získa vo výstupnom diere.

Môže vám slúžiť: červený trpaslík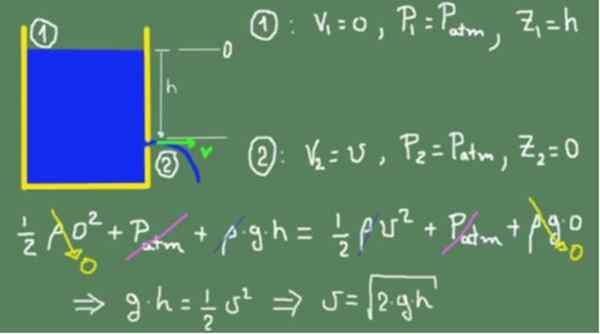

Predchádzajúce políčko ukazuje, že získaný výsledok je rovnaký ako výsledok objektu, ktorý voľne padá,

S tým, čo sa demonštruje, princíp Torricelli.

Vyriešené cvičenia

Cvičenie 1

Jo) Malá výstupná trubica vodnej nádrže je 3 m pod hladinou vody. Vypočítajte rýchlosť výstupu vody.

Riešenie:

Nasledujúci obrázok ukazuje, ako sa na tento prípad aplikuje Torricelliho vzorec.

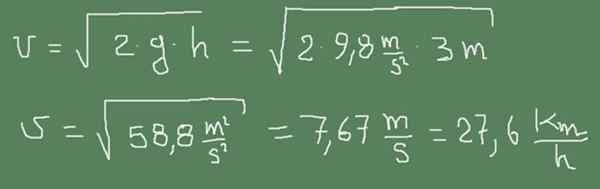
Cvičenie 2

Ii) Za predpokladu, že výstupná trubica predchádzajúcej cvičebnej nádrže má priemer 1 cm, vypočítajte prietok výstupu vody.

Riešenie:

Prietok je objem kvapaliny, ktorá vychádza na jednotku času a je jednoducho vypočítaná vynásobením výstupnej plochy otvoru výstupnou rýchlosťou.

Nasledujúci obrázok zobrazuje podrobnosti výpočtu.

Cvičenie 3

Iii) Určite, ako výška je voľný povrch vody v nádobe, ak je to známe

že v diere na spodnej časti nádoby sa voda dostane na 10 m/s.

Riešenie:

Aj keď je otvor na spodnej časti nádoby, je možné aplikovať Torricelliho vzorec.

Nasledujúci obrázok ukazuje detail výpočtov.

Odkazy

1. Wikipedia. Torricelliova veta.
2. Hewitt, P. Koncepčná fyzická veda. Piaty vydanie.119.
3. Mladý, Hugh. 2016. Sears-Zansky's University Physics s modernou fyzikou. 14. vydanie. Pearson. 384.