Steiner Vysvetlenie veta, aplikácie, cvičenia

On Steinerova veta, tiež známy ako veta paralelnej osi, Umožňuje vyhodnotiť okamih zotrvačnosti predĺženého tela, okolo osi, ktorá je rovnobežná s inou, ktorá prechádza stredom hmotnosti objektu.

Objavil ho švajčiarsky matematický_Cm moment zotrvačnosti objektu vzhľadom na os, ktorá prechádza cez jeho CM a ja masové centrum_z moment zotrvačnosti vzhľadom na inú paralelnú os k tomu.

postava 1. Obdĺžnikové dvere zapínanie svojich radostí majú okamih zotrvačnosti, ktorú je možné vypočítať pomocou Steinerovej vety. Zdroj: Pixabay.

Známa vzdialenosť D, ktorá oddeľuje obe osi a hmotnosť m od príslušného tela, moment zotrvačnosti vzhľadom na os inkognito je:

Jo_z = I_Cm + Md²

Moment zotrvačnosti naznačuje, aké ľahké je pre objekt otáčať sa okolo určitej osi. Závisí to nielen od tela tela, ale aj od toho, ako sa distribuuje. Z tohto dôvodu je známy tiež ako Rotačná zotrvačnosť, Byť vašimi jednotkami v medzinárodnom systéme KG . m².

Veta ukazuje, že moment zotrvačnosti Jo_z Je to vždy väčšie ako moment zotrvačnosti Jo_Cm v sume danej M.D².

[TOC]

Žiadosti

Keďže objekt je schopný otáčať sa okolo mnohých osí a v tabuľkách zvyčajne iba okamih zotrvačnosti, pokiaľ ide o os, ktorá prechádza cez ťažisko, Steinerova veta uľahčuje výpočet, keď potrebuje otáčať telá na nápravách na nápravách, ktoré sa nezhodujú tak.

Môže vám slúžiť: priamy pohyb: Charakteristiky, typy a príklady

Napríklad dvere sa bežne neotávajú okolo osi, ktorá prechádza cez jej hmotnostné centrum, ale vzhľadom na bočnú os, kde pánty priľnú.

Pri poznaní momentu zotrvačnosti je možné vypočítať kinetickú energiu spojenú s rotáciou na tejto osi. Jo Klimatizovať je kinetická energia, Jo moment zotrvačnosti okolo príslušnej osi a Ω Splní sa uhlová rýchlosť, ktorá:

K = ½ i.Ω²

Táto rovnica je veľmi podobná veľmi známemu vzorcu kinetickej energie pre hromadný objekt M Pohybovanie rýchlosťou vložka:  K = ½ m.vložka². A je to okamih zotrvačnosti alebo rotačnej zotrvačnosti Jo hrá v rotácii rovnakú úlohu ako cesto M Preklad.

Demonštrácia Steinerovej vety

Moment zotrvačnosti rozšíreného objektu je definovaný ako:

I = ∫r² Dm

Kde Dm Je to nekonečná hmota hmotnosti a r Je to vzdialenosť medzi Dm a os rotácie z. Na obrázku 2 táto os prechádza stredom hmotnosti CM, môže to však byť ktokoľvek.

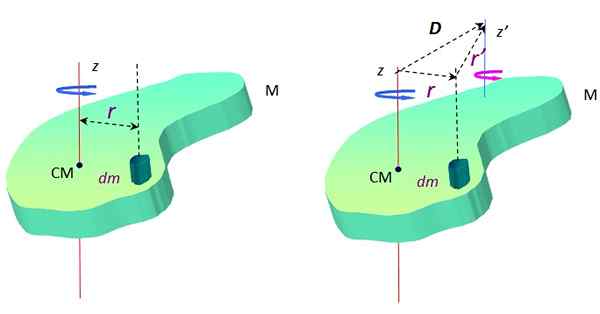Obrázok 2. Objekt rozšírený v rotácii okolo dvoch paralelných osí. Zdroj: f. Zapata.

Okolo inej osi  z ', Moment zotrvačnosti je:

Jo_z= ∫ (R ')² Dm

Teraz, podľa trojuholníka tvoreného vektormi D, r a R ' (Pozri obrázok 2 vpravo), existuje vektorový súčet:

r + R ' = D   → R ' = D - r

Tri vektory sú v rovine objektu, ktorý môže byť Xy. Pôvod súradnicového systému (0,0) sa vyberie v cm na uľahčenie nasledujúcich výpočtov.

Týmto spôsobom štvorcový modul vektora R ' je:

Môže vám slúžiť: Biofyzika: História, aké štúdie, aplikácie, koncepty, metódy

(R ')² = (D_X- r_X)² +(D_a - r_a)² =

= D_X² + D_a² +r_X² + r_a2 -2d_Xr_X - 2 d_ar_a =

= D² + r²  - 2d_Xr_X - 2 d_ar_a

Teraz sa tento vývoj nahradí v integráli momentu zotrvačnosti I_z a tiež sa používa definícia hustoty dm = ρ.Dv:

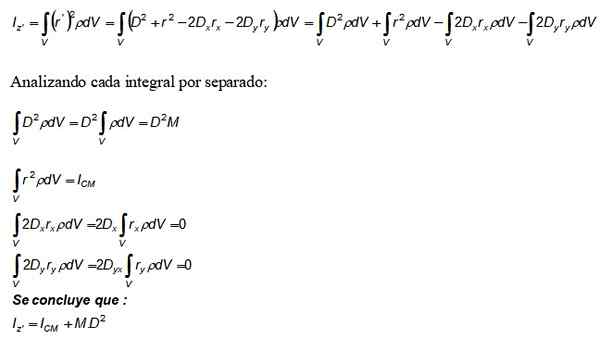
Termín m. D² ktorý sa objavuje v Steinerovej vete pochádza z prvého integrálu, druhý je okamih zotrvačnosti týkajúcej sa osi, ktorá prechádza cez CM.

Pokiaľ ide o svoju časť, tretí a štvrtý integrál má hodnotu 0, pretože podľa definície tvoria polohu CM, ktorá bola vybraná ako pôvod súradníckeho systému (0,0).

Vyriešené cvičenia

-Cvičenie vyriešené 1

Obdĺžnikové dvere na obrázku 1 majú hmotnosť 23 kg, 1,30 širokú a vysokú 2,10 m. Určite okamih zotrvačnosti dverí týkajúcich sa osi, ktorá prechádza radosťou, za predpokladu, že dvere sú tenké a jednotné.

Obrázok 3. Schéma pre príklad vyriešená 1. Zdroj: Upravené pixabay.

Riešenie

Z tabuľky momentov zotrvačnosti, pre obdĺžnikovú dosku hmoty ma a rozmery do a b, Moment zotrvačnosti vzhľadom na os, ktorá prechádza cez jej ťažkú ​​hmotu, je: i_Cm = (1/12)M(do² + b²).

Predpokladajú sa homogénne dvere (prístup, pretože dvere postavy pravdepodobne nie sú až toľko). V tomto prípade prechádza centrum masy cez geometrické centrum. Na obrázku 3 bola nakreslená os, ktorá prechádza cez hmotnostné centrum, a ktorá je tiež rovnobežná s osou, ktorá prechádza radosťou.

Jo_Cm = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Môže vám slúžiť: Čo je to geoid?

Aplikácia Steinerovej vety na os zelenej rotácie:

I = i_Cm + Md² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Cvičenie vyriešené 2

Nájdite moment zotrvačnosti tenkej homogénnej tyče, keď sa točí vzhľadom na os, ktorá prechádza jedným z jej koncov, pozri obrázok. Je to väčšie alebo menej ako moment zotrvačnosti, keď sa točí okolo svojho centra? Pretože?

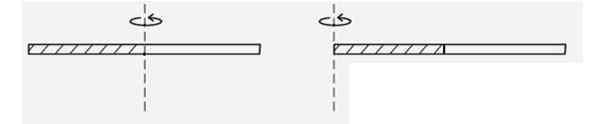Obrázok 4. Schéma pre príklad vyriešené 2. Zdroj: f. Zapata.

Riešenie

Podľa momentov zotrvačnosti, okamih zotrvačnosti Jo_Cm tenkej tyče cesta M a dĺžka L je: Jo_Cm = (1/12) ml²

A Steinerova veta uvádza, že keď sa otáča okolo osi, ktorá prechádza cez jeden koniec d = l/2, zostáva:

I = i_Cm + Md² = (1/12) ml² + M (l/2)² = (1/3) ml²

Je to staré.

Vplyv vzdialenosti od osi rotácie nie je lineárny, ale kvadratický. Hmota, ktorá je dvojnásobkom vzdialenosti, ktorú bude mať iná moment zotrvačnosti úmernej (2d)² = 4D².

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 313-340.
2. Gruzínska štátna univerzita. Rotačný pohyb. Získané z: Phys.Nthu.Edu.Twar.
3. Veta paralelnej osi. Obnovené z: hyperfyziky.Fytrický.Gsu.Edu.
4. Rex, a. 2011. Základy fyziky. Pearson. 190-200.
5. Wikipedia. Veta paralelnej osi. Zdroj: In.Wikipedia.orgán