História molekulárnej kinetickej teórie, postuláty a príklady

Ten Molekulárna kinetická teória Je to ten, ktorý sa snaží vysvetliť experimentálne pozorovania plynov z mikroskopického hľadiska. To znamená, že sa snaží spájať povahu a správanie plynných častíc, s fyzikálnymi charakteristikami plynu ako tekutiny; Vysvetlite makroskopické z mikroskopických.

Plyny boli vždy predmetom záujmu vedcov kvôli ich vlastnostiam. Zaberajú celý objem kontajnera, v ktorom sú, sú schopní úplne komprimovať bez toho, aby ich obsah bol proti nižšiemu odporu; A ak sa teplota zvyšuje, nádoba sa začne rozširovať a môže dokonca prasknúť.

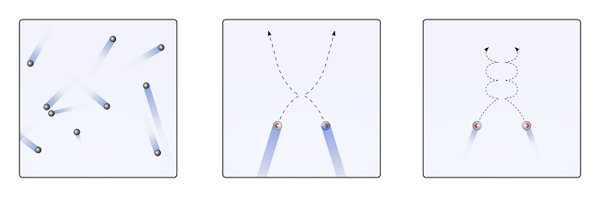Plynné častice vo vzdialených podmienkach alebo blízko skvapalnenia. Zdroj: Olivier Cleynen a užívateľ: Sharayanan [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Mnohé z týchto vlastností a správania sú zhrnuté v zákonoch ideálnych plynov. Považujú však plyn za celok a nie za súbor miliónov dispergovaných častíc vo vesmíre; Okrem toho neposkytuje, z údajov tlaku, objemu a teploty, viac informácií o tom, ako sa tieto častice pohybujú.

Je to tak, že molekulárna kinetická teória (TCM) ich navrhuje vizualizovať ako mobilné gule (vynikajúci obraz). Tieto gule sa zrazia navzájom a steny svojvoľne a udržiavajú lineárnu trajektóriu. Keď sa však teplota klesá a tlak sa zvyšuje, trajektória guľôčok sa stáva krivkou.

Plyn podľa TCM sa musí správať ako sféry prvého obrázkového boxu. Ale keď sa ochladí a zvýši tlak na ne, ich správanie sa pohybuje od ideálu. Sú to potom skutočné plyny, blízko skvapalnenia a idú do kvapalnej fázy.

Za týchto podmienok sa interakcie medzi guľami stávajú dôležitejším. Čím bližšie sú z skvapalnenia, tým viac kriviek ich trajektórií (pravý box) a ich zrážky sú menej energie.

[TOC]

História

Daniel Bernoulli

Myšlienku týchto sfér, lepšie nazývaných atómy, už zvážil rímsky filozof Lucretius; Nie pre plyny, ale pre pevné, statické objekty. Na druhej strane, v roku 1738 Daniel Bernoulli aplikoval atómové videnie na plyny a tekutiny tým, že si ich predstavoval ako nepokojné sféry, ktoré sa pohybujú vo všetkých smeroch.

Jeho práca však v tom čase porušila fyzické zákony; Telo sa nemohlo pohybovať večne, takže nebolo možné myslieť si, že súbor atómov a molekúl sa navzájom zrazil bez straty energie; to znamená, že existencia elastických zrážok nebola možná.

Rudolf Clausius

O storočie neskôr ostatní autori posilnili TCM modelom, v ktorom sa plynné častice pohybovali v jednom smere. Rudolf Clausius však zostavil svoje výsledky a vyzbrojil úplnejší model TCM, s ktorým sa snažil vysvetliť ideálne zákony o plyne, ktoré preukázali Boyle, Charles, Dalton a Avogadro.

Môže vám slúžiť: Coulombimetria: Základy, typy, aplikácie

James Clerk Maxwell a Ludwig Boltzmann

V roku 1859 James Clerk Maxwell uviedol, že plynné častice vykazujú rozsah rýchlosti pri danej teplote a že ich sada sa dá zvážiť pomocou priemernej molekulárnej rýchlosti.

Potom v roku 1871 Ludwig Boltzmann spojil existujúce nápady s entropiou a ako termodynamicky vždy má tendenciu zaberať maximálny možný priestor homogénnym a spontánnym spôsobom.

Postulácia molekulárnej kinetickej teórie

Zvážiť plyn z jeho častíc, model, v ktorom sú splnené určité postuláty alebo predpoklady; Predpokladá sa, že logicky by malo byť schopné predpovedať a vysvetliť (čo najvernejšie) makroskopické a experimentálne pozorovania. To znamená, že postuláty TCM sú uvedené a opísané.

Objem plynných častíc je zanedbateľný

V nádobe plnom plynných častíc sa rozptýlia a pohybujú sa medzi nimi cez všetky rohy. Keby sa na chvíľu mohli stretnúť v konkrétnom bode nádoby, bez skvapalnenia, bolo by pozorované, že sotva zaberajú opovrhnuteľnú časť objemu nádoby.

To znamená, že v nádobe, aj keď obsahuje milióny plynných častíc, je skutočne viac prázdna ako úplná (pomer objemu a vačí oveľa menej ako 1); Preto, ak to jeho prekážky dovolia, môže byť on a plyn vo vnútri náhle stlačené; Pretože v úvahách sú častice veľmi malé, rovnako ako ich objem.

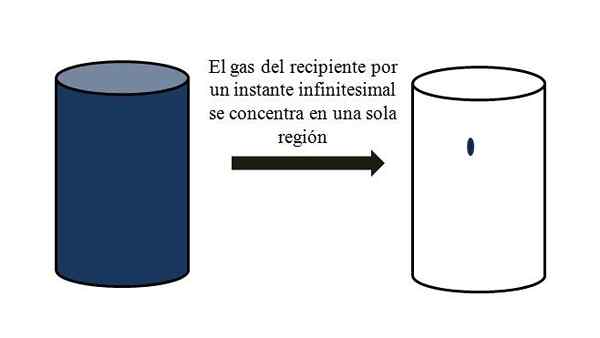Objem-vacío Vzťah plynu v nádobe. Zdroj: Gabriel Bolívar.

Vynikajúci obraz presne ilustruje, čo je uvedené vyššie, pomocou modroodného plynu.

Príťažlivé sily medzi časticami sú nulové

Plynné častice vo vnútri nádoby sa navzájom zrážajú bez dostatočného času na to, aby sa ich interakcie stali silou; Ešte menej, keď to, čo ich hlavne obklopuje, je molekulárny prázdny. Okamžitým dôsledkom je to, že ich lineárne trajektórie im umožňujú úplne pokryť objem kontajnera.

Keby vyššie uvedené neboli tak, „bizarný“ a „labyrintický“ nádoba by mala v mokrých oblastiach v dôsledku kondenzácie plynu; Namiesto toho častice cestujú po celej nádobe s plnou slobodou, bez toho, aby ich ich interakcie zastavili.

Môže vám slúžiť: kyselina chlorovodíka (HCLO3) Vyradenia plynných častíc, keď sú interakcie nulové alebo zanedbateľné (do., lineárne) a keď sú dôležité (b., krivky). Zdroj: Gabriel Bolívar.

Lineárne trajektórie horného obrázka (a.) demonštrovať tento postulát; Zatiaľ čo ak sú trajektórií krivky (b.), dôkaz, že existujú interakcie, ktoré medzi časticami nemožno ignorovať.

Plynné častice sú vždy v pohybe

Od prvých dvoch postelátov sa zbližujú navyše skutočnosť, že častice plynu sa nikdy neprestanú pohybovať. Po rozmazaní v nádobe sa zrazia navzájom a so stenami ich, s silou a rýchlosťou priamo úmernou k absolútnej teplote; Táto sila je tlak.

Keby sa plynné častice prestali pohybovať okolo chvíle, bolo by svedkom vo vnútri „dymových jazykov“, ktoré vyplynuli z ničoho, s dostatočným časom na to, aby sa objednali vo vákuu a dali náhodné cesty.

Zrážky medzi časticami a stenami nádoby sú elastické

Ak sa elastické zrážky medzi plynnými časticami a stenami nádoby nikdy nevyskytnú v nádobe, nikdy sa nevyskytne (zatiaľ čo sa fyzikálne podmienky nezmenia) kondenzácia plynu; Alebo to, čo je to isté ako tvrdenie, že nikdy ne odpočívajú a vždy sa zrážajú.

Je to tak preto, že pri elastických zrážkách nedochádza k čistej strate kinetickej energie; Častica sa zráža so stenou a odrazí sa rovnakou rýchlosťou. Ak sa častica pri zrážke znižuje rýchlosť, druhá sa zrýchľuje, bez tepla alebo zvuku, ktorý rozptyľuje kinetickú energiu ktorejkoľvek z nich.

Kinetická energia nezostáva konštantná

Pohyb častíc je náhodný a chaotický, takže nie všetci majú rovnakú rýchlosť; ako sa to používa napríklad na diaľnici alebo v dave. Niektoré sú energickejšie a cestujú väčšiu rýchlosť, zatiaľ čo iné sú pomalé a čakajú na zrážku, aby ich zrýchlili.

Na opis vašej rýchlosti je potom potrebné vypočítať priemer; A tým sa získa priemerná kinetická energia častíc alebo molekúl plynu. Pretože kinetická energia všetkých častíc sa neustále mení, priemer umožňuje lepšiu kontrolu údajov a môžete pracovať s väčšou spoľahlivosťou.

Priemerná kinetická energia sa rovná danej teplote pre všetky plyny

Priemerná molekulárna kinetická energia (EC_Mp) V nádobe je upravený s teplotou. Pri vyššej teplote bude táto energia vyššia. Pretože je to priemer, môžu existovať častice alebo sóda, ktoré majú v súvislosti s touto hodnotou väčšiu alebo menšiu energiu; niektoré rýchlejšie a pomalšie.

Môže vám slúžiť: kyseliny a základy: rozdiely, charakteristiky, príklady

Matematicky sa dá preukázať, že EC_Mp Závisí to výlučne od teploty. To znamená, že nezáleží na tom, čo je plyn, jeho molekulárna hmotnosť alebo štruktúra, EC_Mp Bude to rovnaké pri teplote T a bude sa meniť iba vtedy, ak sa zvýši alebo klesne. Zo všetkých postulátov je to možno najrelevantnejšie.

A čo priemerná molekulárna rýchlosť? Na rozdiel od ES_Mp, Molekulárna hmotnosť ovplyvňuje rýchlosť. Čím ťažšie je molekula častíc alebo plynu, je prirodzené očakávať, že sa bude pohybovať pomalšie.

Príklady

Nižšie sú uvedené niekoľko krátkych príkladov toho, ako sa TCM podarilo vysvetliť zákonom ideálnych plynov. Aj keď sa neriešia, s TCM sa dajú vysvetliť aj iné javy, ako napríklad šírenie a výtok plynov.

Boyle zákon

Ak je objem nádoby stlačený pri konštantnej teplote, vzdialenosť, ktorú sa musia zrážať plynnými časticami, sa musí zraziť, aby sa zrazila proti stenám; čo sa rovná zvýšeniu frekvencie týchto kolízií, čo vedie k väčšiemu tlaku. Keď je teplota konštantná, EC_Mp Je tiež konštantná.

Charles zákon

Ak t, EC sa zvyšuje_Mp sa zvýši. Plynné častice sa budú pohybovať rýchlejšie a zrazia sa väčší počet stien nádoby; Zvyšuje tlak.

Ak sú steny flexibilné, schopné rozširovať sa, jeho oblasť sa zväčší a tlak klesne, kým sa nestane konštantným; V dôsledku toho sa zvýši objem.

Daltonov zákon

Keby sa do priestrannej nádoby pridalo niekoľko litrov rôznych plynov, z menších kontajnerov by sa ich celkový vnútorný tlak rovný súčtu čiastočných tlakov vyvíjaných každým typom plynu osobitne.

Pretože? Pretože všetky plyny sa začínajú navzájom zrážať a homogénne sa rozptyľujú; Interakcie medzi nimi sú neplatné a vákuum prevláda v nádobe (postuláty TCM), takže je to tak, akoby sa každý plyn našiel sám, čo vyvíja jeho tlak jednotlivo bez rušenia ostatných plynov.

Odkazy

1. Whitten, Davis, Peck & Stanley. (2008). Chémia. (8. vydanie.). Cengage Learning, str. 426-431.
2. Fernández Pablo. (2019). Molekulárna kinetická teória. Vino. Obnovené z: VIX.com
3. Jones, Andrew Zimmerman. (7. februára 2019). Kinetická molekulárna teória plynov. Zotavené z: Thoughtco.com
4. Sála Nancy. (5. mája 2015). Kinetická teória plynov. Glenn Research Center. Zdroj: GRC.hrniec.Vláda
5. Vlk. A nižšie S. (9. októbra 2018). Základy kinetickej molekulárnej teórie. Chémia librettexts. Získané z: Chem.Librettexts.orgán
6. Kinetická molekulárna teória. Zdroj: Chemed.Chem.Purdue.Edu
7. Wikipedia. (2019). Kinetická teória plynov. Zdroj: In.Wikipedia.orgán
8. Tobolka. (s.F.). Kinetická molekulárna teória plynov. Získané z: Toppr.com