Súčet Riemannovej histórie, vzorcov a vlastností, cvičení

Ten Riemann Sum Je to názov, ktorý prijíma približný výpočet definovaného integrálu pomocou diskrétnej sumy s konečným číslom výrazu. Bežnou aplikáciou je prístup oblasti funkcií v grafiku.

Bol to nemecký matematik Georg Friedrich Bernhard Riemann (1826-1866), ktorý prvýkrát ponúkol prísnu definíciu integrálu funkcie v danom intervale. Oznámil to v článku uverejnenom v roku 1854. 

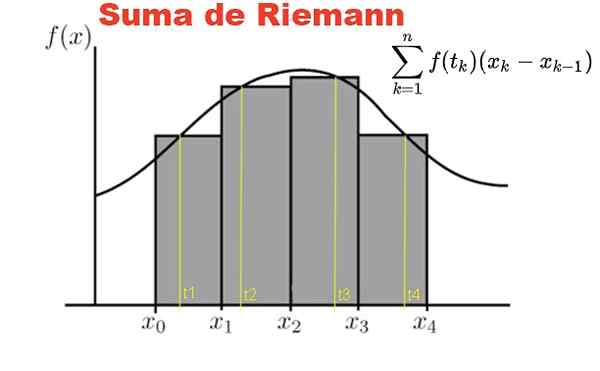
postava 1. Riemannova suma je definovaná na funkcii F a oddielu v intervale [x0, x1]. Zdroj: Fanny Zapata.

Riemannova suma je definovaná na funkcii y = f (x), pričom x patrí do uzavretého intervalu [a, b]. V tomto intervale sa vytvorí oddiel P prvkov N:

P = x₀= a, x₁, X₂,…, X_n= b

To znamená, že interval je rozdelený nasledovne:

 Tu t t_{klimatizovať} je medzi x_K-1 a x_{klimatizovať}:

X_K-1 ≤ t_{klimatizovať} ≤ x_{klimatizovať}

Obrázok 1 zobrazuje súčet Riemanna funkcie F v intervale [x₀, X₄] Na oddiele štyroch subintervalov, sivých obdĺžnikov.

Súčet predstavuje celkovú plochu obdĺžnikov a výsledkom tohto súčtu je numericky prístupy k oblasti pod krivkou F, medzi Abscissas x = x₀ y x = x₄.

Prístup k oblasti pod krivkou sa samozrejme výrazne zlepšuje v rozsahu, v akom je číslo n oddielov je väčší.  Týmto spôsobom sa suma konverguje do oblasti pod krivkou, keď číslo n oddiely majú tendenciu nekonečno.

[TOC]

Vzorce a vlastnosti

Riemannova súčet funkcie F (x) na oddiele:

Môže vám slúžiť: Rhomboid: Charakteristiky, ako vytiahnuť obvod a oblasť

P = x₀= a, x₁, X₂,…, X_n= b

Definované v intervale [a, b], je daný:

S (p, f) = ∑_{K = 1}ⁿ f (t_{klimatizovať}) (X_{klimatizovať} - X_K-1) 

Kde t_{klimatizovať} Je to hodnota v intervale [x_{klimatizovať}, X_K-1]. V súčte Riemanna sa zvyčajne používajú pravidelné intervaly šírky Δx = (b - a)/n, kde a a b sú minimálne a maximálne hodnoty Abscissa, zatiaľ čo n je počet podskupín.

V takom prípade Riemannova správna suma je:

SD (f, n) = [f (a+δx)+f (a+2Ax)+…+f (a+(n-1) δx)+f (b)]*δx

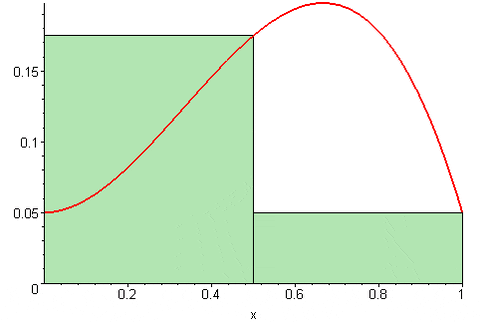Obrázok 2. Riemannova správna suma. Zdroj: Wikimedia Commons. 09glasgow09 [CC By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)].

Kým Riemannova ľavá suma Je vyjadrené ako:

Áno (f, n) = [f (a)+f (a+δx)+…+f (a+(n-1) δx)]*δx

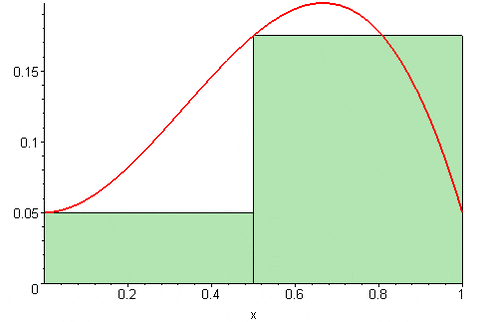Obrázok 3. Súčet Riemann odišiel. Zdroj: Wikimedia Commons. 09glasgow09 [CC By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)]

Konečne Riemann Central Sum je:

Sc (f, n) = [f (a+δx/2)+f (a+3Ax/2)+…+f (b- δx/2)]*δx

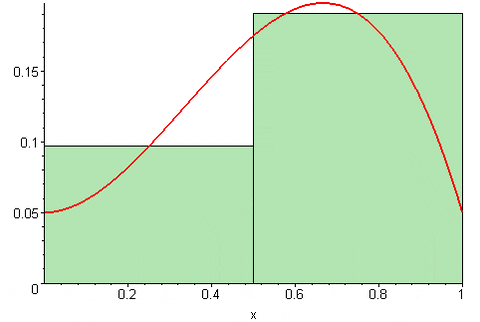Obrázok 4. Stredná suma Riemanna. Zdroj: Wikimedia Commons. 09glasgow09 [CC By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0)]

V závislosti od toho, kde sa nachádza bod T_{klimatizovať} V intervale [x_{klimatizovať}, X_K-1] Riemannova suma môže nadhodnotiť alebo podceňovať presnú hodnotu oblasti pod krivkou funkcie y = f (x) (x). To znamená, že obdĺžniky môžu vyniknúť z krivky alebo byť trochu pod týmto.

Oblasť pod krivkou

Hlavnou vlastnosťou súčtu Riemanna a ktorej sa jej dôležitosť stáva, že ak má počet pododdiele tendenciu k nekonečnu, výsledok súčtu sa konverguje k definovanej integráli funkcie:

Predchádzajúci výraz zodpovedá definícii Riemannovho integrálu a uplatňuje sa za predpokladu, že funkcia F je kontinuálna a mäkká. Pre viac konkrétnych funkcií existujú aj ďalšie definície integrálu (integrál de statieldjes a integrál de lebesgue).

Môže vám slúžiť: Štandardná chyba odhadu: Ako sa vypočítava, príklady, cvičenia

Vyriešené cvičenia

- Cvičenie 1

Vypočítajte hodnotu integrálu definovaného medzi a = -2 až b = +2 funkcie:

f (x) = x²

Využite súčet Riemann. Ak to chcete urobiť, nájdite sumu pravidelných oddielov intervalu [a, b] a potom preberte matematický limit pre prípad, že počet oddielov ukladá do nekonečna. 

Riešenie

Toto sú kroky, ktoré treba nasledovať:

-Po prvé, interval oddielu je definovaný ako: 

Δx = (b - a)/n. 

-Potom je súčet Riemanna vpravo zodpovedajúci funkcii F (x) ako je tento:

-Teraz sú vymenené a = -2 a b =+2, takže interval alebo krok δx = 4/n. To znamená, že súčet Riemanna pre funkciu f (x) = x² je:

-Potom sa vyvinie štvorcový binomén: 

[-2 +(4i/n)]² = 4 - (16 i /n) + (4 /n)² Jo²

-A potom je starostlivo nahradený v súde:

-Ďalším krokom je oddelenie súhrnov a odstránenie konštantných množstiev ako spoločný faktor každej sumy. Je potrebné vziať do úvahy, že index je I, preto čísla a podmienky s n Sú považované za konštantné:

-Každá suma sa hodnotí, pretože pre každú z nich existujú vhodné výrazy. Napríklad prvé zo zhrnutí da n:

Druhý je:

 A tretí je:

 -Nahradenie výsledkov súhrnov v súčte Riemanna sa konečne získa:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Nakoniec musíte vypočítať integrál je:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5,333

Čitateľ môže overiť, či ide o presný výsledok, ktorý sa dá získať riešením neurčitej integrálnej integrálnej a vyhodnotenia limitov integrácie podľa pravidla Barrow.

Môže vám slúžiť: Ako previesť z km/h a m/s? Vyriešené cvičenia

- Cvičenie 2

Určite približne oblasť pod funkciou: 

f (x) = (1/√ (2π) e^(-X2/2)

Medzi x = -1 a x =+1, pomocou centrálneho súčtu Riemanna s 10 oddielmi. Porovnajte s presným výsledkom a odhadnúť percentuálny rozdiel.

Riešenie

Krok alebo zvýšenie medzi dvoma následnými diskrétnymi hodnotami je:

Δx = (1 - (-1)/10 = 0,2

Takže oddiel P, na ktorom sú definované obdĺžniky, je takto:

P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1,0

Ale ako chcete, je centrálna suma, funkcia F (x) sa vyhodnotí v stredných bodoch subintervalov, to znamená v sade:

T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.

Riemannova suma (centrálna) je takáto:

S = f (-0,9)*0,2 +f (-0,7)*0,2 +f (-0,5)*0,2 +… +f (0,7)*0,2 +F (0,9)*0,2

Pretože funkcia F je symetrická, je možné znížiť súčet iba na 5 termínov a výsledok sa vynásobí dvoma:

S = 2*0,2*f (0,1)+ f (0,3)+ f (0,5)+ f (0,7)+ f (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Funkcia uvedená v tomto príklade nie je nič iné ako dobre známy Gauss Bell (normalizovaný, s priemernou rovnou nulou a štandardnou odchýlkou). Je známe, že oblasť pod krivkou v intervale [-1,1] pre túto funkciu je 0,6827.

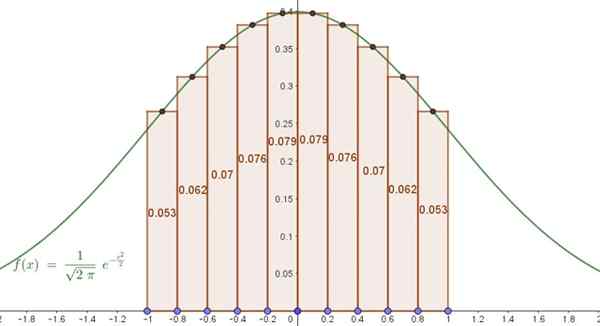Obrázok 5. Oblasť pod približným zvonom Gaussom pomocou súčtu Riemanna. Zdroj: f. Zapata.

To znamená, že približné riešenie s iba 10 výrazmi sa zhoduje s presným riešením až do troch desatinných miest. Percentuálna chyba medzi približným integrálom a presným je 0,07%.

Odkazy

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Komplexný výpočet (ilustrované ed.). Madrid: ESIC Editorial.
2. Jednoznačný. História koncepcie integrálu. Získané z: úložiska.Jednoznačný.je
3. Uis. Sumy Riemann. Obnovené z: matematiky.Uis.Edu.co
4. Wikipedia. Riemann Sum. Obnovené z: je.Wikipedia.com
5. Wikipedia. Integrácia Riemann. Obnovené z: je.Wikipedia.com