Priamy a polotovarový segment

Čiara línie a poloworght sú diferencované v tom, že segment čiary je obmedzený; to znamená, že ich počiatočný bod a ich konečný bod sú známe. Od polo -pravosti je známy jeho počiatočný bod, ale nie jeho konečný bod, pretože sa rozširuje na nekonečno.

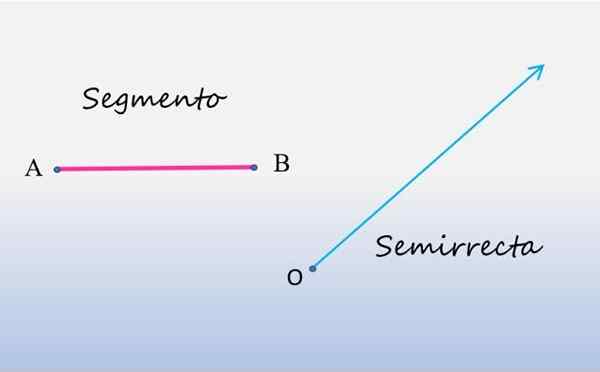
Nasledujúci obrázok zobrazuje vľavo, segment čiary a vpravo, polopriepustné:

Segment a polo. Zdroj: f. Zapata.

Ako je zrejmé, segment je línia čiary, ktorá začína v bode A a končí v bode B, tieto body sú koncami uvedeného segmentu. Meranie segmentu zodpovedá dĺžke medzi jeho koncami.

Pokiaľ ide o svoju stranu, má semifónny východiskový bod v bode o a rozširuje sa na nekonečno, čo je rovnocenné s tvrdením, že je obmedzený iba jedným koncom, zvyčajne nazývaný pôvod. Z tohto dôvodu sa tiež nazývajú Môj bože.

Segmenty sú označené písmenami, ktoré označujú počiatočný bod a koniec. Napríklad segment obrázku je segment AB, alebo sa na vrchu umiestni mŕtvica, ako je tento:

Na druhej strane je možné vymenovať aj polotovary, ktoré naznačujú bod zodpovedajúci pôvodu a druhý ďalší list. Môže sa použiť aj malý list na reprezentáciu blesku alebo polo -regulácie a existujú aj polotovary s vlastným menom, ako bude vidieť v príkladoch neskôr.

Príklady segmentov

Segmenty sú veľmi dôležité v geometrii, nižšie sú niektoré z najpozoruhodnejších:

Strany mnohouholníka

Polygóny sú ploché a uzavreté figúrky, ktorých strany sú nekontrolované segmenty linky. Napríklad trojuholník má tri strany, štvoruholník má štyri strany, Pentagon má päť a tak ďalej.

Môže vám slúžiť: Tesseldos: Charakteristika, typy (pravidelné, nepravidelné), príklady

Priemer obvodu

Je definovaný ako tento segment, ktorý obsahuje dva body obvodu a nevyhnutne prechádza centrom toho istého.

Lano obvodu

Keď segment, ktorý sa pripojí k dvom bodom obvodu, neprechádza jeho stredom, nazýva sa lano.

Výška trojuholníka

Výška trojuholníka je definovaná ako segment, ktorý prechádza kolmo z jednej zo strán trojuholníka do opačného vrcholu. Ak je miera základne trojuholníka, nazývaná B a výška toho istého, označená ako H, je známa, oblasť A je vypočítaná prostredníctvom známeho vzorca:

A = ½ b ∙ h

Semirret príklady

Semi -prúžky sú tiež veľmi dôležitými prvkami v geometrii. Niektoré dobre známe semifinále sú:

Pozitívne semi -menságy

Tri smery vo vesmíre: vysoká, široká a hĺbka, môže byť reprezentovaná systémom karteziánskych osí, pozostávajúcich z troch vzájomne kolmých čiar medzi sebou, označený ako osi ako osi X, a a z, ktoré sú rezané v bode, ktorý sa volá pôvod.

Toto ustanovenie rozdeľuje priestor na osem regiónov známych ako Oktavery. Na nasledujúcom obrázku sú pozorované pozitívne poloory X, a a z, ktoré určujú prvý ocant. Podobne pozitívny semi -x y y určuje oblasť roviny s názvom Prvé kvadrant.

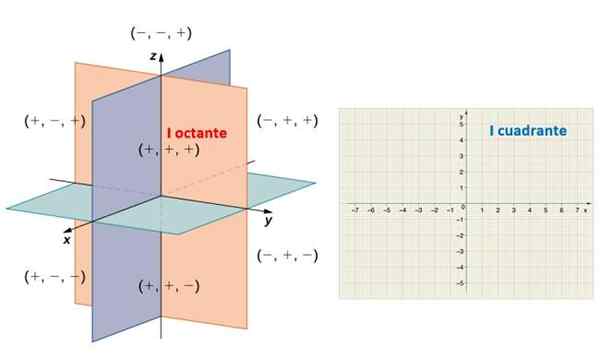Vľavo, osem oktátov priestoru a doprava, karteziánska rovina sa rozdelila na štyri kvadranty. Zdroj: matematické librettyxts.

Strany uhla

Uhol je zlomok lietadla, ktorý je vymedzený dvom. Tento spoločný bod je vrchol uhlu, zatiaľ čo polo -prúdi. Takéto ustanovenie je znázornené na nasledujúcom obrázku:

Môže vám slúžiť: Aký je vzťah medzi oblasťami Rhombus a obdĺžnik?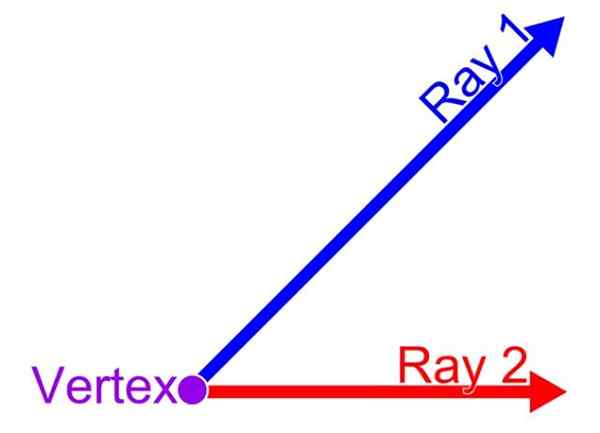 Prvky uhla. Zdroj: Wikimedia Commons.