Sarrus Pravidlo

Sarrus Pravidlo. Zdroj: Používateľ: Sevela.P, CC BY-SA 4.0, Wikimedia Commons

Čo je to Sarrusovo pravidlo?

Ten Sarrus Pravidlo Je to technika na výpočet determinantov štvorcovej matrice 3 × 3 alebo väčšie. Tento systém umožňuje ľahšie riešenie. Používa sa tiež na určenie, či sú sady vektorov lineárne nezávislé a vytvorili základňu vektorového priestoru.

Tieto aplikácie sú založené na inverzibilite matíc. Ak je matica pravidelná, jej determinant sa líši od 0. Ak je jedinečný, jeho determinant má hodnotu 0. Determinanty sa dajú vypočítať iba v štvorcových matici.

Na výpočet matíc ľubovoľnej objednávky je možné použiť Laplaceovu vetu. Táto veta nám umožňuje zjednodušiť matice vysokých rozmerov, v sumách malých determinantov, ktoré sa rozkladáme z hlavnej matrice.

Uvádza, že determinant matrice sa rovná súčtu produktov každého riadku alebo stĺpca determinantom jej pripojenej matrice.

To znižuje determinanty, takže determinant stupňa N sa stane determinantami N-1. Ak toto pravidlo uplatňujeme postupným spôsobom, môžeme získať determinanty dimenzie 2 (2 × 2) alebo 3 (3 × 3), kde je jeho výpočet oveľa jednoduchší.

Sarrus Pravidlo

Pierre Frederic Sarrus (1798-1861) bol francúzsky matematik. Väčšina svojich matematických zmlúv je založená na metódach rozlíšenia rovníc a výpočtu variácií v rámci numerických rovníc.

V jednej z jeho zmlúv vyriešil jednu z najkomplexnejších záhad mechaniky. Na vyriešenie problémov kĺbových kusov, Sarrus zaviedol transformáciu alternatívnych priamých pohybov v rovnomerných kruhových pohyboch. Tento nový systém je známy ako mechanizmus Sarrus.

Môže vám slúžiť: externalizácia a internalizácia nákladov

Výskum, ktorý mu dal najviac, bol ten, v ktorom predstavil novú metódu výpočtu determinantov, v článku „Nouvelles Methodes pour la résolution des équations“ („Nová metóda rozlíšenia rovníc“), uverejnené v roku 1833. Tento spôsob riešenia lineárnych rovníc je známy ako Sarrus Rule.

Pravidlo Sarrus umožňuje vypočítať determinant matice 3 × 3 bez použitia Laplaceovej vety, zavedenie oveľa jednoduchšej a intuitívnejšej metódy. 

Aby sme boli schopní overiť hodnotu pravidla Sarrus, berieme akúkoľvek maticu dimenzie 3:

Výpočet jeho determinantu by bol vyrobený z produktu jeho hlavných diagonálov a odpočítal produkt od inverzných diagonálov. Toto by bolo nasledujúce:

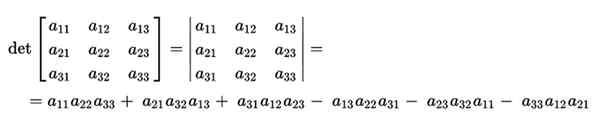
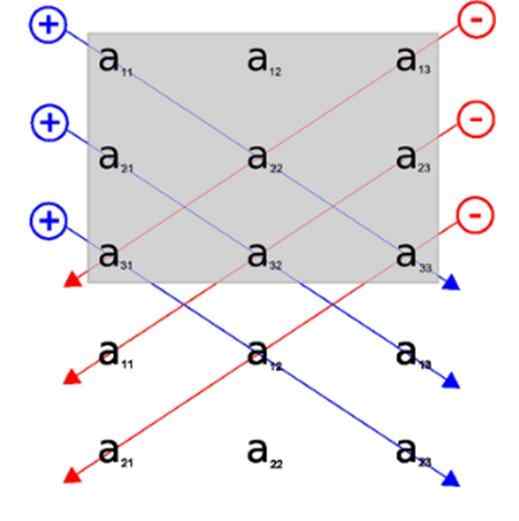
Pravidlo Sarrus nám umožňuje získať oveľa jednoduchšie videnie pri výpočte diagonálov determinantu. Zjednodušilo by sa to pridaním prvých dvoch stĺpcov do zadnej časti matrice.

Týmto spôsobom je jasnejšie o svojich hlavných diagonáloch a ktoré inverzné, pre výpočet produktu.

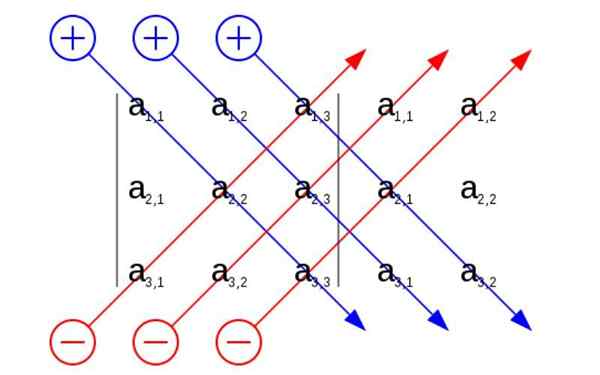
Prostredníctvom tohto obrázka vidíme aplikáciu pravidla Sarrus, zahrnujeme riadok 1 a 2 pod grafickou reprezentáciou počiatočnej matrice. Týmto spôsobom sú hlavnými uhlopriečkami tri diagonály, ktoré sa objavujú na prvom mieste.

Tri inverzné diagonály sú zase tie, ktoré sa objavujú ako prvé vzadu.

Týmto spôsobom sa diagonály objavujú vizuálnejším spôsobom bez komplikujúceho rozlíšenia determinantu a snažia sa zistiť, ktoré prvky matrice patria ku každému diagonálne.

Môže vám slúžiť: Quechua Slová preložené do španielčiny

Ako sa zdá na obrázku, vyberieme si diagonály a vypočítame produkt vyplývajúci z každej funkcie. Diagonály, ktoré sa objavujú modrou farbou, sú tie, ktoré sa sčítavajú. K ich súčtu odpočítame hodnotu diagonálov, ktoré sa objavujú v červenej farbe.

Aby bola kompresia jednoduchšia, môžeme použiť numerický príklad namiesto použitia algebraických výrazov a podmienečných výrazov.

Ak vezmeme napríklad maticu 3 × 3, napríklad:

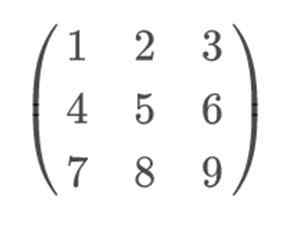
Ak chcete uplatniť pravidlo Sarrus a vyriešiť ho vizuálnejším spôsobom, mali by sme zahrnúť riadok 1 a 2, ako riadok 4 a 5. Je dôležité udržiavať riadok 1 v 4. pozícii a riadok 2 v 5. Pretože ak ich vymeníme, pravidlo Sarrus nebude účinné.

Na výpočet determinantu by naša matica bola nasledovná:

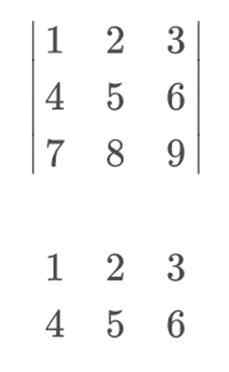
Ak chcete pokračovať pri výpočte, vynásobíme prvky hlavných diagonálov. Zosúvajúce, že začnú vľavo.

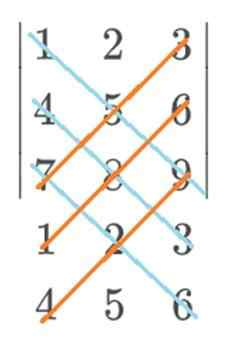
V tomto príklade by modrá išla s pozitívnym znamením a červená s negatívnym znakom. Konečný výpočet pravidla Sarrus by zostal týmto spôsobom:

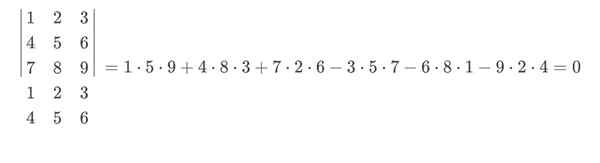
Chlapci determinantov

Determinant rozmeru 1

Ak je dimenzia matrice 1, matica je týmto spôsobom: a = (a)

Preto by jeho determinant bol nasledujúci: deta (a) = | a | = a

Zhrnuté, determinant matice A sa rovná absolútnej hodnote matice A, ktorá je v tomto prípade.

Determinant rozmer 2

Ak pôjdeme na matice dimenzie 2, získame matice typu:

Môže vám slúžiť: Tauticgy

Kde je jeho determinant definovaný ako:

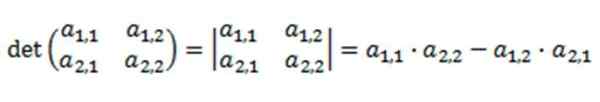
Rozlíšenie tohto determinantu je založené na množení jeho hlavnej diagonálnej, odčítavajúc produkt jeho inverznej diagonálu.

Determinant rozmeru 3

Ak je dimenzia matrice 3, výsledná matica by bola tohto typu:

Determinant tejto matice by sa týmto spôsobom vyriešil prostredníctvom pravidla Sarrus:

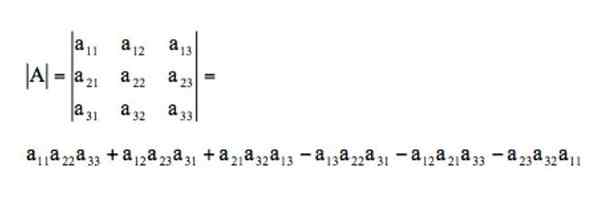
Odkazy

1. Anthony Nicolaides (1994). Determinanty a matice. Publikácia.
2. M. Casteleiro Villalba (2004). Úvod do lineárnej algebry. Redakcia.