Korešpondenčné pravidlo funkcie

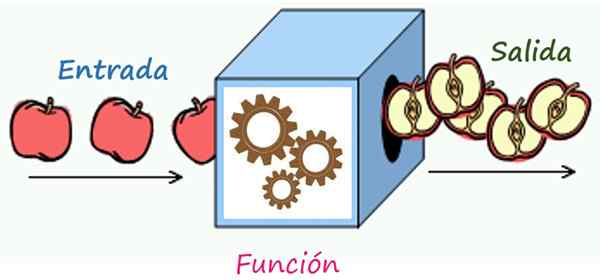
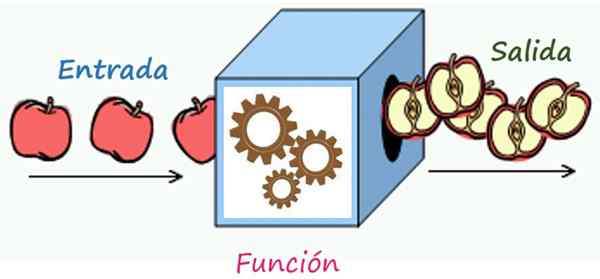Pravidlo korešpondencie je mechanizmus, ktorý transformuje prvky vstupu do výstupných prvkov. Zdroj: Wikimedia Commons/F. Zapata

Aké je pravidlo korešpondencie funkcie?

Ten korešpondenčné pravidlo funkcie Poukazujte na spôsob, akým sú prvky jednej sady spojené s prvkami druhého. Prvky prvého súboru sú známe ako oblasť, a tým druhým, ako Kodominium ani protichodný.

Vzťah alebo spojenie medzi množinami sa dá špecifikovať verbálnym alebo písomným pokynom, keď sú sady číselné, pravidlo korešpondencie je označené vzorcom.

Tento vzorec obsahuje operácie, ktoré sa musia vykonávať s prvkami počiatočnej zostavy, a tak získajte sériu prvkov zahrnutých v kodomínii.

Teraz, keď je vzťah medzi prvkami funkciou, pravidlo korešpondencie spĺňa dve osobitné podmienky:

• Pre každý z prvkov domény je prostredníctvom pravidla korešpondencie spojený jediný prvok kodominium, známy ako predstavovať.
• Tento obrázok je jedinečný, inými slovami, žiadny prvok domény nie je spojený s viac ako jedným prvkom Codominium.

Týmto spôsobom si viete predstaviť pravidlo korešpondencie funkcie ako mechanizmu zamknutého v krabici. Hodnota každej domény, bez výnimky, môže zadať políčko a dostať sa z neho transformovaná prostredníctvom operácií označených pravidlom korešpondencie. Príklady sa zobrazia okamžite.

Príklady

Príklad 1

Pravidlo korešpondencie funkcie môže byť vyjadrené ako písomná inštrukcia, keď prvky nie sú číselné.

Napríklad existuje súbor krajín označených ako P a ďalší súbor miest C:

Môže vám slúžiť: U -test z Mann - Whitney: Čo je to a keď sa uplatňuje, vykonanie, príklad

P = Kanada, Mexiko, Španielsko, USA, Francúzsko, Argentína, Brazília, Nemecko

C = Paríž, Londýn, Buenos Aires, Berlín, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Rím, Brasília, Toronto

Byť pravidlom korešpondencie F Medzi p a c daným:

F: P → C

Kde F Je to pravidlo „... ktorého kapitál je .. ”, Ktorý spája každú krajinu v P (štartovacia súprava), s hlavným mestom v C (súbor príchodu).

Napríklad: „Španielsko, ktorého kapitál je Madrid ". Prvok „Španielsko“ patrí do štartovacej sady P a prvok „madrid“ k celému C, príchodu.

Reprezentácia tejto funkcie sa dá vykonávať prostredníctvom Venn diagramu alebo jednoducho pomocou usporiadaných párov.

Objednané páry obsahujú, ako už názov napovedá, dva prvky s konkrétnym poriadkom, v tomto príklade je prvým prvkom páru krajina a druhé, jej hlavné mesto.

Pokiaľ ide o svoju časť, Diagram Venn je spôsob, ako vizualizovať funkciu, ukazovať štartovacie a príchodové sady, ako aj pravidlo korešpondencie medzi nimi.

Zastúpenie F ako usporiadaných párov

F = (Kanada, Ottawa); (Mexiko, Mexico City); (Španielsko Madrid); (USA; Washington); (Paríž, Francúzsko); (Argentína Buenos Aires); (Brazília Brazília); (Nemecko, Berlín)

Prvý pár spolupracuje Kanada, ktorého kapitál je Ottawa, druhý spolupracovník Mexiko, ktorého kapitál je Mexico City a tak ďalej.

Zastúpenie F ako Venn Diagram

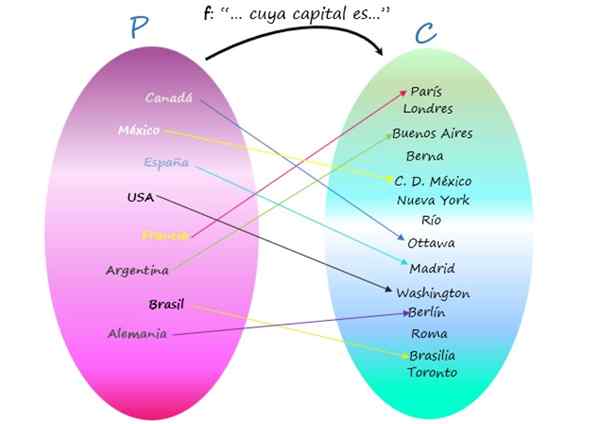
Všimnite si, že existujú mestá, ktoré nie sú hlavným mestom žiadnej krajiny, pretože hoci sú prvkami kodominia, nie sú obrazom žiadneho prvku počiatočnej sady. Napriek tomu je vzťah funkciou, pretože dôležité je, že každá krajina má svoj kapitál, a to je jedinečné.

Môže vám slúžiť: Oblasť pravidelného a nepravidelného Pentagónu: Ako sa užíva, cvičenia

Podskupina tvorená prvkami kodomínium, ktoré sú obrazom nejakého prvku domény, sa nazýva rozsah alebo funkcia funkcie. Napríklad cesta r F je:

R = Paríž, Buenos Aires, Mexico City, Ottawa, Madrid, Berlín, Washington, Brasilia

Stojí za to sa opýtať, či je možné nadviazať vzťah medzi C a P, kde sa C stáva štartovacou setou a príchodom. Odpoveď znie áno, ale nebola by to funkcia, pretože existujú mestá, ktoré nie sú hlavnými mestami, ako napríklad New York alebo krajina, ktorej je hlavným mestom, sa neobjavuje medzi prvkami komplexu P, ako je Rím, napríklad Rím.

Príklad 2

Ak sú sada odchodu a súprava príchodu číselné, pravidlo korešpondencie funkcie, ktorá ich spája, je vzorec. Napríklad buďte majstrovstvom funkcie nasledujúca sada:

D = 0, 1, 2, 3, 4, 5, 6)

Pravidlo korešpondencie F: D → R, ktorý spája prvky D so sadou skutočných čísel R je:

F: „Dvojité“

Ak je „x“ prvkom počiatočnej sady, F (x) je zodpovedajúci prvok množiny príchodu a pravidlo korešpondencie je napísané takto:

f (x) = 2x

Codominium je sada skutočných čísel. Podskupina Reais je cesta tejto funkcie, sada čísel, ktorých hodnota je dvakrát ako x:

R = 0, 2, 4, 6, 8, 10, 12

Vo forme usporiadaných párov vedie pravidlo korešpondencie v:

F = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Objednané páry môžu byť grafom v karteziánskej rovine. Prvý prvok krútiaceho momentu je umiestnený na horizontálnej osi, tiež nazývaná osi Abscissas alebo osi „x“, zatiaľ čo druhý ide na zvislú os, os usporiadanej alebo jednoducho osi „y“:

Môže vám slúžiť: distribučný majetok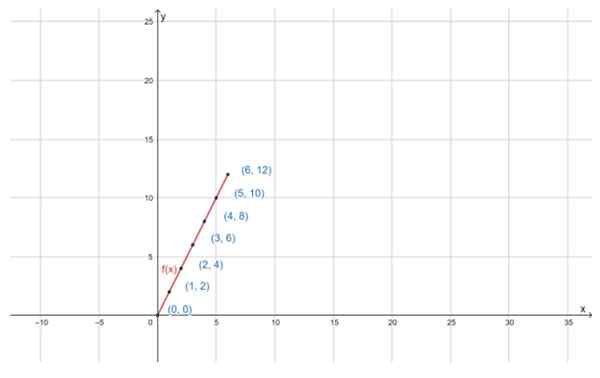 Graf funkcie f (x) = 2x pre zadanú doménu D je priamka. Zdroj: f. Zapata cez geogebra

Cvičenia

Určite pravidlo korešpondencie pre nasledujúce vzťahy, čo naznačuje, či sú alebo nie sú funkcie alebo nie. Sada prírodných čísel je n a súbor skutočného je r.

Uveďte aj doménu, kodominium a cestu funkcie, v prípadoch, v ktorých zodpovedá:

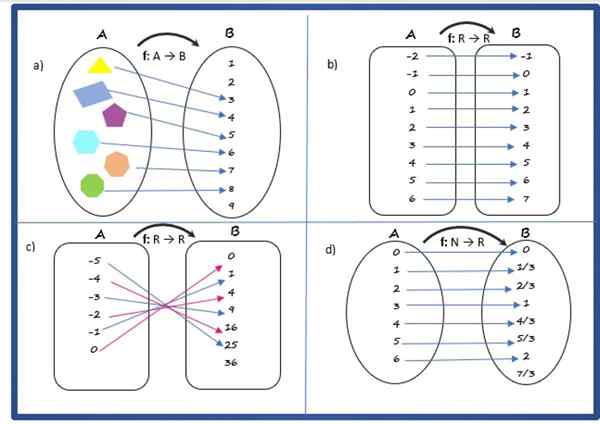
Roztok

Je to funkcia, pretože každý prvok počiatočnej sady, pozostávajúca z polygónov, má v súprave príchodu jedinečný obraz.

Pravidlo korešpondencie súvisí s polygónom s počtom jeho strán, doména pozostáva zo súboru A polygónov:

A = trojuholník, štvorkoliek, Pentagon, hexagon, heptagon, osemuholník

Codominium je sada prvých prírodných čísel vrátane 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

A CO C sú prírodné čísla od 3 do 8:

C = 3, 4, 5, 6, 7, 8

Riešenie B

Je to funkcia, pretože spĺňa vyššie uvedené podmienky.

Pravidlo korešpondencie je:

f (x) = x + 1

Pravidlo korešpondencie naznačuje, že funkcia je definovaná r → r, preto je doménou sada skutočných čísel. A co -oominium a trasa sa tiež zhodujú so skutočným.

Riešenie c

Je to funkcia s pravidlom korešpondencie:

f (x) = x²

Doména a kodomínium sú stanovené reais, ale trasa pozostáva iba z pozitívnych reálnych čísel, označovaných ako r⁺ a vrátane 0.

Riešenie d

Je to funkcia. Jeho korešpondenčné pravidlo je:

f (x) = x/3

Jeho doména je sada prírodných čísel n a kodominium, ako aj trasa, sú skutočné n čísla r.