Druhé riadky

Drevo dverí tejto záhrady je ochotné takým spôsobom, že určujú suché čiary. Zdroj: f. Zapata. Pxhere.com

Aké sú suché čiary?

V lietadle Druhé riadky Sú to tie, ktoré pretínajú ďalšie čiary a krivky. V prípade dvoch riadkov je jeho križovatka bodom, zatiaľ čo sekundová čiara v krivke to znižuje v dvoch alebo viacerých bodoch.

Opatrne sledujte plot hornej postavy. Na ňom bolo nakreslené niekoľko priamych farieb, označovaných ako l₁, L₂ a l₃. Šípky na oboch stranách znamenajú, že čiary sú predĺžené neurčito.

No, riadky L₁, L₂ a l₃ Sušia sa navzájom, pretože každý z nich je rezaný vo fialových bodoch.

Okrem toho čiary L₁ a l₂, Ako l₁ a l₃, Určujú 4 uhly medzi sebou, dva z nich akútne a druhé tupé, zatiaľ čo čiary L₂ a l₃ Sú kolmé, čo znamená, že 4 uhly určené nimi sú rovné.

Dve paralelné čiary nemôžu byť nikdy suché, pretože kvôli svojmu stavu nemajú žiadne náhodné body. Zhodujúce čiary naopak nie sú suché, pretože majú viac ako jeden bod spoločného bodu.

Charakteristiky sušiacich línií

• Ako križovatka majú jedinečný bod.
• Svahy dvoch sušiacich čiary musia byť odlišné. Áno m₁ Je to sklon čiary l₁, a m₂ Je to sklon čiary l₂, potom je splnené, že m₁ ≠ m₂.
• Svahy dvoch sušiacich línií kolmých na seba, ktorých príslušné svahy sú m₁ a m₂, Spĺňajú vzťah m₁ = -1/ m₂. Okrem toho skalárny produkt medzi dvoma vektormi vložka a alebo obsiahnuté v týchto riadkoch je nulové, pretože definícia skalárneho produktu je vložka alebo = v ∙ u ∙ cos θ, keď je 9 uhol medzi vektormi.
• Čiara môže byť sekundárna k krivke alebo inej geometrickej postave.
• Pri pretínaní, dve sušovacie čiary generujú 4 uhly, identické dva až dva alebo identické navzájom identické.

Môže vám slúžiť: frakčné rovnice

Ako zistiť, či sú dve čiary suché

Z vyššie uvedených charakteristík sušiacich línií je možné stanoviť tri kritériá, aby ste vedeli, či sú dve čiary suché:

-Porovnanie svahov. Ak sa líšia, čiary sú suché.

-Vykonávanie skalárneho produktu medzi dvoma vektormi, ktoré sú obsiahnuté v týchto riadkoch, nazývané Režisér. Ak je skalárny produkt neplatný, čiary sú suché a kolmé a ak nie je nulové, je možné poznať minimálny uhol medzi nimi, čo je akútny uhol existujúce medzi čiarami.

Za predpokladu, že tento uhol sa líši od 0 °, čiary sú suché a ak sú rovné 0 °, potom sú rovnobežné čiary.

-Priamo výpočet akútneho uhol, ktorý existuje medzi čiarami, pozná ich svahy. To sa dá dosiahnuť prostredníctvom vzorca, ktorý sa týka dotyčnice uvedeného uhla so svahmi.

Nech maj m₁ a m₂ svahy a 9 medzi nimi akútny uhol. Tangen θ je daný:

Typy sušiacich riadkov

Keď sa navzájom sušia dve riadky, môžu to byť nasledujúce typy:

• Šikmý, Ak pri rezaní tvoria dva akútne uhly a dva tupé uhly. Tieto uhly sú doplnkové, to znamená súčet miery uhla plus jeden z tupých uhlov sa rovná 180 °. Celkovo sa súčet 4 uhlov rovná 360 °.
• Kolmý, Tie, ktoré pretína 4 uhly rovnajúce sa 90 °.

Ako nájsť križovatku medzi dvoma riadkami

Ak sušia dve čiary, majú iba jeden bod rezov, ktorý rieši systém dvoch lineárnych rovníc s dvoma neznámymi. Ak sú čiary dané všeobecne: AX + BU = C, uvedený systém rovníc je:

Môže vám slúžiť: nekonečná súprava: Vlastnosti, príklady

do₁x + b₁ y = c₁

do₂x + b₂ y = c₂

Ako nájsť križovatku medzi čiarom a krivkou

Poznanie rovníc čiary aj krivky je navrhnutý systém rovníc a ktorého riešenia zodpovedajú križovatkovým bodom. Ak systému chýba riešenie, čiara nie je sekundárna k krivke, ani ak existuje jediný bod rezania, pretože v takom prípade je čiara tankovaná k krivke.

Aby sa linka vysušila, ako je uvedené na začiatku, musí mať systém rovníc dve alebo viac riešení.

Príklady sušenia riadkov

Karteziánske lietadlo

Karteziánska rovina je určená dvoma riadkami, nazývané X os x a Os y, horizontálne a vertikálne. Tieto čiary sú kolmé a ich bod križovatky sa nazýva Pôvod koordinovaného systému, alebo jednoducho pôvod.

Diagonál polygónu

Polygón je plochá postava troch alebo viacerých strán, ktoré sa spájajú v bodoch nazývaných vrcholy. Segment, ktorý sa spájal s dvoma nekonečnými vrcholmi, je diagonál polygónu a čiara obsahujúca uvedený segment je sekundárny k príslušnému polygónu.

Obvodové lano

Lano obvodu je segment, ktorý sa spája s dvoma jeho bodmi. Hlavným lanom je priemer, ktorý nevyhnutne prechádza stredom obvodu. Čiara, ktorá obsahuje akékoľvek lano, vrátane priemeru, je sušiacimi čiarami k obvodu.

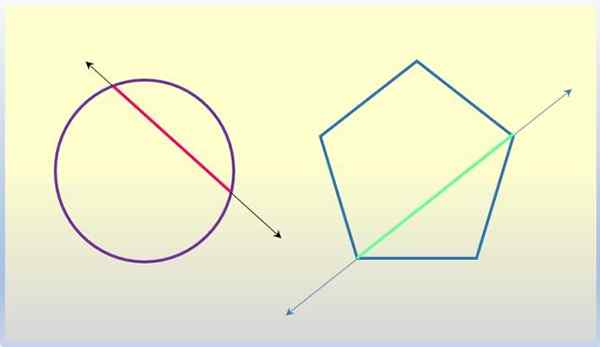Druhé riadky k geometrickým figúram. Zdroj: f. Zapata.

Krížový kľúč

S týmto nástrojom sú matice, ktoré držia pneumatiky na kolesách vozidiel. Ramená tvoria čiary, ktoré sú suché a zároveň kolmé.

Môže vám slúžiť: Proporcionálna variácia

Texty abecedy

Niektoré písmená abecedy pozostávajú z priamych ťahov, ktoré určujú secant. Napríklad písmeno X sa skladá z dvoch úderov, ktoré sú rozrezané v jednom bode a písmeno T pozostáva z dvoch kolmých čiar.

Vyriešené cvičenia

Cvičenie 1

Zistite, či riadky dané:

L₁ : y = 5x - 3

L₂ : y = -2x+1

Riešenie

Sklon čiary uvedenej vo forme y = mx + b je hodnota m, to znamená koeficient, ktorý sprevádza x. Pretože m₁ = 5 a m₂ = -2, ktoré sa líšia, dospelo sa k záveru, že čiary sú suché.

Cvičenie 2

Aký je akútny uhol medzi riadkami cvičenia 1?

Riešenie

Hodnoty m sa priamo vymenia₁ = 5 a m₂ = -2 vo vzorci uvedenom v predchádzajúcich častiach:

Preto je uhol medzi čiarami 9 = arctg 0.777… = 37.9 °.

Cvičenie 3

Aká je priesečník medzi čiarami predchádzajúcich cvičení?

Riešenie

Systém rovníc sa navrhuje nasledovne:

Ktorého riešenie je: x = 4/7; y = -1/7 (môže byť vyriešené ktorýmkoľvek z metód rozlíšenia pre rovničné systémy alebo s kalkulačkou).

Preto je bod priesečníka riadkov: P (4/7; -1/7).

Odkazy

1. Analytická geometria.Info. Druhé riadky. Získané z: geometriaanalitiky.Info.
2. Larson, R. 2006. Výpočet analytickou geometriou. 8. Vydanie. McGraw Hill.
3. Linky, ktoré krížia. Získané z: Teacheraltuna.com.
4. Requena, b. Druhé riadky. Získané z: Universoformulas.com.
5. Villena, m. Analytická geometria v R3. Zdroj: DSPACE.Espol.Edu.ES.