Aká je lineárna rýchlosť? (S vyriešenými cvičeniami)

Ten Lineárna rýchlosť Je definovaný ako to, čo je vždy tangenciálne pre trajektóriu, po ktorej nasleduje častica, bez ohľadu na to. Ak sa častica vždy pohybuje v rektilineárnej trajektórii, nie je problém si predstavovať, ako je sprevádzaný vektor rýchlosti.

Vo všeobecnosti sa však pohyb vykonáva na krivke svojvoľne. Každá časť krivky môže byť modelovaná, akoby bola súčasťou rádiového kruhu do, ktorý v každom bode je dotyk.

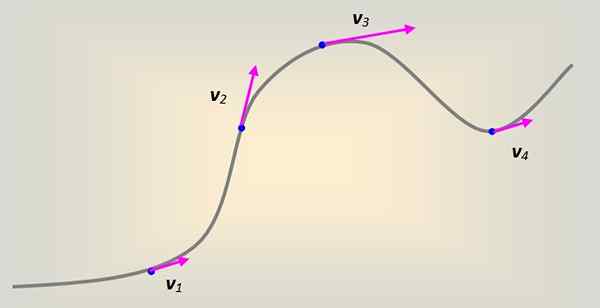
postava 1. Lineárna rýchlosť na mobile, ktorá popisuje krivočiaru trajektórie. Zdroj: Self Made.

V tomto prípade je lineárna rýchlosť sprevádzaná tangenciálne a vždy k krivke v každom bode.

Matematicky okamžitá lineárna rýchlosť je derivát polohy vzhľadom na čas. Byť r polohový vektor častíc v okamihu tón, Potom je lineárna rýchlosť daná výrazom:

vložka = r'(T) = dr / dt

To znamená, že lineárna rýchlosť alebo tangenciálna rýchlosť, ako sa nazýva, nie je nič iné ako zmena polohy vzhľadom na čas.

[TOC]

Lineárna rýchlosť v kruhovom pohybe

Keď je pohyb na obvode, môžeme ísť vedľa častice v každom bode a zistiť, čo sa deje v dvoch veľmi špeciálnych smeroch: jeden z nich je ten, ktorý vždy ukazuje na stred. Toto je adresa radiálny.

Ďalším dôležitým smerom je ten, ktorý sa odohráva pri obvode, toto je adresa tangenciálny A lineárna rýchlosť ju vždy má.

Môže vám slúžiť: manometrický tlak: vysvetlenie, vzorce, rovnice, príklady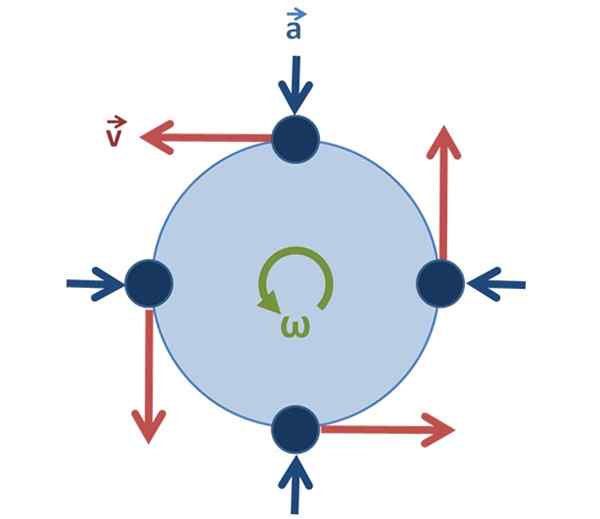Obrázok 2. Rovnomerný kruhový pohyb: Vektor rýchlosti mení smer a smer, keď sa častica otáča, ale jej veľkosť je rovnaká. Zdroj: Originál od používateľa: Brews_ohare, Svged by user: SjLegg [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)].

V prípade rovnomerného pohybu kruhového pohybu je dôležité, že je nezmenený.

Pre tento pohyb je poloha ako funkcia času daná S (t), kde siež je on Zájazdový oblúk a tón Je čas. V takom prípade je okamžitá rýchlosť daná výrazom V = ds/dt A je to konštantné.

Ak sa rozsah rýchlosti tiež líši (už vieme, že smer to vždy robí, inak sa mobil nemohol otočiť), čelíme rôznym kruhovým pohybom, počas ktorého je mobilný okrem otáčania, môže zastaviť alebo zrýchliť.

Lineárna rýchlosť, uhlová rýchlosť a centripetálne zrýchlenie

Pohyb častíc je možné vidieť aj z hľadiska zametací uhol, Namiesto toho, aby to robil z cieľa, cestoval. V tomto prípade sa hovorí o uhlová rýchlosť. Pre pohyb v rádiovom kruhu R, Existuje vzťah medzi oblúkom (v radiánoch) a uhlom:

S = r 9

Odvodenie vzhľadom na obe strany:

ds/dt = r (dθ/dt)

Volanie derivátu 9 vzhľadom na tón ako uhlová rýchlosť A označovanie grécke písmenom Ω „Omega“, máte tento vzťah:

v = ΩR

Zrýchlenie

Každý kruhový pohyb má zrýchlenie, to je vždy smerované do stredu obvodu. Dá sa postarať o to, že sa rýchlosť mení, aby sa pohybovala s časticou, keď sa otáča.

Môže vám slúžiť: Kalibračná krivka: Na čo je to, ako to urobiť, príklady

Zrýchlenie do_c ani do_R Vždy poukazuje na stred (pozri obrázok 2) a týmto spôsobom súvisí s lineárnou rýchlosťou:

do_c = v² /R

A s uhlovou rýchlosťou ako:

do_c = (ΩR)² /R = Ω²R

Pre rovnomerný pohyb kruhu, poloha S (t) Je to forma:

S (t) = So+ VT

Okrem toho rôzny kruhový pohyb musí mať súčasť zrýchlenia nazývaného Tangenciálne zrýchlenie do_Tón, ktorá sa zaoberá zmenou rozsahu lineárnej rýchlosti. Jo do_Tón  Je to konštantné, Pozícia je:

S (t) = s_ani + vložka_aniT + ½ a_Tóntón²

S vložka_ani Rovnako ako počiatočná rýchlosť.

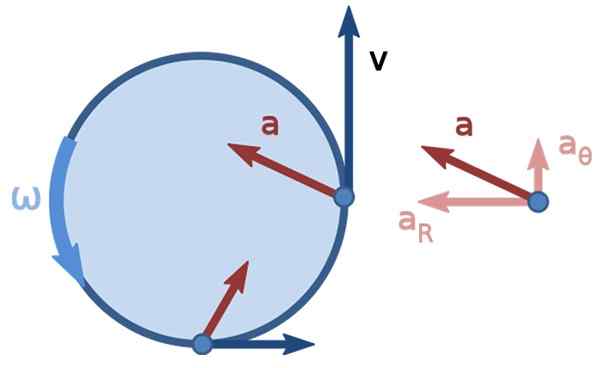Obrázok 3. Neuniformný kruhový pohyb. Zdroj: Nonuniform_Circular_Motion.PNG: Brews Oharedorivave Work: Kooning Jons [CC BY-SA 3.0 (https: // creativeCommons.Org/licencie/By-SA/3.0)].

Vyriešené cvičenia lineárnej rýchlosti

Vyriešené cvičenia prispievajú k objasneniu správneho použitia uvedených pojmov a rovníc.

-Cvičenie vyriešené 1 

Hmyz sa pohybuje na polkruhu polomeru r = 2 m, začínajúc od odpočinku v bode a pri zvyšovaní jeho lineárnej rýchlosti, rýchlosťou p m/s². Nájdite: a) Po tom, kedy dosiahne bod B, b) vektor lineárnej rýchlosti v tomto okamihu, c) vektorové zrýchlenie v tom okamihu.

Obrázok 4. Hmyz začína od A a dosahuje B na polkruhovej trajektórii. Má lineárnu rýchlosť. Zdroj: Self Made.

Riešenie

a) Vyhlásenie naznačuje, že tangenciálne zrýchlenie je konštantné a má hodnotu π m/s², Potom je platné použiť rovnicu pre rovnomerne rozmanitý pohyb:

S (t) = s_ani + vložka_aniT + ½ a_Tón.tón²

S S_ani = 0 a V_ani = 0:

S (t) = ½ a_Tón.tón²

S = πR (Polovica dĺžky obvodu)

T = (2. πR /do_Tón) ^½ S = (2π.2 /π)^½S = 2 s

b) v (t) = v_ani + do_Tón. T = 2π pani

Keď je v bode B, vektor lineárnej rýchlosti vo vertikálnom smere dole v smere (-a):

Môže vám slúžiť: Aká je dielektrická konštanta?

vložka (t) = 2π pani(-a)

c) Tangenciálne zrýchlenie už existuje, akcelerácia centripetálneho zrýchlenia má rýchlosť vektora do:

do_c = v² / R = (2π)² / 2 m/ s² = 2π² pani²

do = a_c (-X) + a_Tón (-a) = 2π²(-X)+ π (-a) pani²

-Cvičenie vyriešené 2

Častica sa otočí v rádiovom kruhu 2.90 m. V konkrétnom okamihu je jeho zrýchlenie hodnota 1.05 m/s² v smere, ktorý sa tvorí 32 s smerom pohybu. Nájdite svoju lineárnu rýchlosť na: a) tento okamih, b) o 2 sekundy neskôr za predpokladu, že tangenciálne zrýchlenie je konštantné.

Riešenie

a) Riaditeľstvo hnutia je presne tangenciálna adresa:

do_Tón = 1.05 m/s² . cos 32 ° = 0.89 m/s² ; do_C = 1.05 m/s² . Sen 32 ° = 0.56 m/s²

Rýchlosť čistí do_c = v² / R ako:

v = (r.do_c)^1/2  = 1.27 m/s

b) Rovnica pre rovnomerne rozmanitý pohyb je platná takto: v = v_ani + do_TónT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fyzická séria pre vedu a inžinierstvo. Zväzok 3. Vydanie. Kinematika. 199-232.
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^th… Ed Prentice Hall. 62-64.
4. Relatívny pohyb. Uzdravené z: kurzov.Lumenarning.com
5. Wilson, J. 2011. Fyzika 10. Pearson Vzdelanie. 166-168.