Aká je rovnováha častíc? (S príkladmi)

On rovnováha častíc Je to stav, v ktorom je častica, keď sú vonkajšie sily pôsobiace na nich navzájom zrušené. To znamená, že udržiava konštantný stav, takže sa môže vyskytnúť dvoma rôznymi spôsobmi v závislosti od konkrétnej situácie.

Prvým je byť v statickej rovnováhe, v ktorej je častica nehybná; A druhým je dynamická rovnováha, kde je súčet síl zrušený, ale častica má rovnomerný priamy pohyb.

postava 1. Vyvážiť tvorbu hornín. Zdroj: Pixabay.

Model častíc je veľmi užitočný prístup k štúdiu pohybu tela. Skladá sa z predpokladu, že celá hmotnosť tela je koncentrovaná v jednom bode, bez ohľadu na veľkosť objektu. Týmto spôsobom môžete reprezentovať planétu, auto, elektrón alebo biliardovú guľu.

[TOC]

Výsledná sila

V bode, ktorý predstavuje objekt, je miesto, kde konajú sily, ktoré ich ovplyvňujú. Všetky tieto sily môžu byť nahradené jediným, ktorý robí rovnaký účinok, ktorý sa nazýva výsledná sila ani Čistá sila A je označený ako f_R alebo f_N.

Podľa Newtonovho druhého zákona, keď existuje nevyvážená výsledná sila, telo zažije zrýchlenie úmerné sile:

F_R = m.do

Kde do Je to zrýchlenie, ktoré objekt získava vďaka pôsobeniu sily a m Je to hmotnosť objektu. Čo sa stane, ak telo nie je zrýchlené? Presne to, čo bolo naznačené na začiatku: telo je v pokoji alebo sa pohybuje s rovnomerným priamym pohybom, ktorý nemá zrýchlenie.

Pre rovnováhu s časticami je platné, aby ste sa uistili, že:

F_R = 0

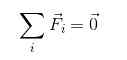
Pretože pridávanie vektorov nevyhnutne neznamená moduly, vektory sa musia rozkladať. Preto je platné vyjadriť:

F_X = m.do_X = 0; F_a = m.do_a = 0; F_z = m.do_z = 0

Diagramy bezplatného tela

Aby sa vizualizovali sily, ktoré pôsobia na časticu, mal by sa vyrobiť diagram voľného tela, v ktorom sú všetky sily pôsobiace na objekt reprezentované šípkami.

Môže vám slúžiť: Zemská magnetosféra: Charakteristiky, štruktúra, plyny

Predchádzajúce rovnice sú vektorová povaha. Rozkladom sily sa vyznačujú znakmi. Týmto spôsobom je možné, že súčet jeho komponentov je nula.

Nasledujú dôležité indikácie, aby bol kresba užitočný:

- Vyberte referenčný systém, v ktorom sa na súradnicových sekách umiestni najväčší počet síl.

- Hmotnosť je vždy nakreslená vertikálne nadol.

- V prípade existencie dva alebo viac povrchov v kontakte sú normálne sily, ktoré sú vždy nakreslené tlačením tela a kolmé na povrch, ktorý ho vyvíja.

- Pre časticu v rovnováhe môže existovať trenie rovnobežné s kontaktným povrchom a proti možnému pohybu, ak sa častica posudzuje v pokoji alebo určite v opozícii, ak sa častice pohybujú s MRU (rovnomerný priamy pohyb).

- Ak je lano, napätie je vždy nakreslené pozdĺž neho a ťahanie tela.

Spôsoby, ako uplatniť stav zostatku

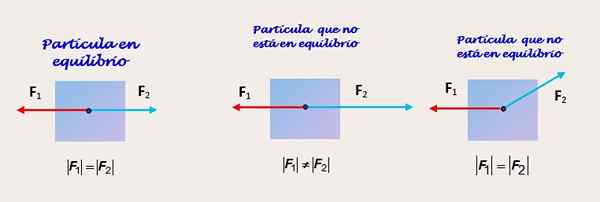Obrázok 2. Dve aplikované sily rôznymi spôsobmi na rovnakom tele. Zdroj: Self Made.

Dve sily rovnakej veľkosti a smeru a opačných zmyslov

Obrázok 2 zobrazuje časticu, na ktorej pôsobia dve sily. Na obrázku vľavo častice prijíma pôsobenie dvoch síl f₁ a f₂ ktorí majú rovnakú veľkosť a konajú rovnakým smerom a v opačných zmysloch.

Častica je v rovnováhe, ale s informáciami za predpokladu, že nie je možné vedieť, či je rovnováha statická alebo dynamická. Je potrebné viac informácií o inerciálnom referenčnom systéme, z ktorého je objekt pozorovaný.

Dve sily rôznych veľkostí, rovnaký smer a opačné zmysly

Obrázok stredu zobrazuje rovnakú častice, ktorá tento čas nie je v rovnováhe, pretože veľkosť sily f₂ je väčší ako f₁. Preto existuje nevyvážená sila a objekt má zrýchlenie v rovnakom smere ako f₂.

Môže vám slúžiť: Darcy Law

Dve sily rovnakej veľkosti a iného smeru

Nakoniec na obrázku napravo pozorujeme telo, ktoré nie je v rovnováhe. Aj keď f₁ a f₂ Majú rovnakú veľkosť, sila f₂ Nie je to v rovnakom smere ako 1. Vertikálna zložka f₂ Nie je to pôsobenie proti žiadnemu inému a častice zažívajú zrýchlenie v tomto smere.

Tri sily s rôznym smerom

Môže byť častice predložené na tri sily v rovnováhe? Áno, pokiaľ pri umiestňovaní špičky každého z nich je výsledná postava trojuholníkom. V tomto prípade je vektorová suma null.

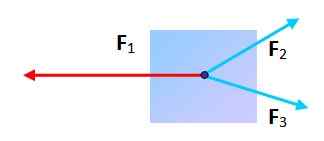Obrázok 3. Častica vystavená pôsobeniu 3 síl môže byť v rovnováhe. Zdroj: Self Made.

Trenie

Sila, ktorá často zasahuje do rovnováhy častíc, je statické trenie. Je to kvôli interakcii objektu predstavovaného časticou s povrchom iného. Napríklad kniha v statickej rovnováhe na naklonenej tabuľke je modelovaná ako častica a má voľný diagram tela, ako je nasledujúce:

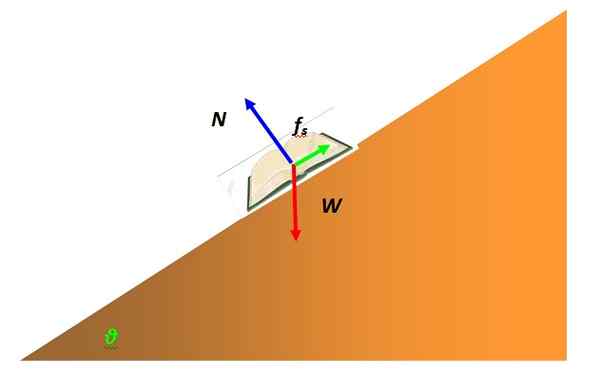Obrázok 4. Diagram bezplatného tela knihy na naklonenej rovine. Zdroj: Self Made.

Sila, ktorá bráni knihe skĺznuť cez povrch naklonenej roviny a zostáva v pokoji, je statické trenie. Závisí to od povahy povrchov v kontakte, ktoré mikroskopicky majú drsnosť s uzamknutými vrcholmi, brániacimi pohybom.

Maximálna hodnota statického trenia je úmerná normálnej sile, ktorá vyvíja povrch na podporovanom objekte, ale kolmá na uvedený povrch. V príklade knihy je uvedené modrou farbou. Matematicky sa vyjadruje takto:

F_viac∝ N

Konštanta proporcionality je Statický koeficient trenia μ_siež, ktorý je experimentálne určený, je bez rozmeru a závisí od povahy povrchov v kontakte.

F_{S max} = μ_siež N

Dynamické trenie

Ak je častica v dynamickej rovnováhe, dochádza k pohybu a statické trenie nezasahuje viac. Ak je prítomná nejaká trecia sila, ktorá je proti pohybu, pôsobí dynamické trenie, ktorých veľkosť je konštantná a daná:

Môže vám slúžiť: Aké sú tepelné vlastnosti a čo sú? (S príkladmi)

F_{klimatizovať} = μ_{klimatizovať} N

Kde μ_{klimatizovať} je on koeficient, čo tiež závisí od typu povrchov v kontakte. Rovnako ako koeficient statického trenia, je bez rozmeru a jeho hodnota sa určuje experimentálne.

Hodnota dynamického koeficientu trenia je zvyčajne menšia ako hodnota statického trenia.

Vyriešený príklad

Kniha na obrázku 3 je v pokoji a má hmotnosť 1.30 kg. V lietadle má uhol sklonu 30 °. Nájdite statický koeficient trenia medzi knihou a povrchom roviny.

Riešenie

Je dôležité zvoliť príslušný referenčný systém, pozri nasledujúci obrázok:

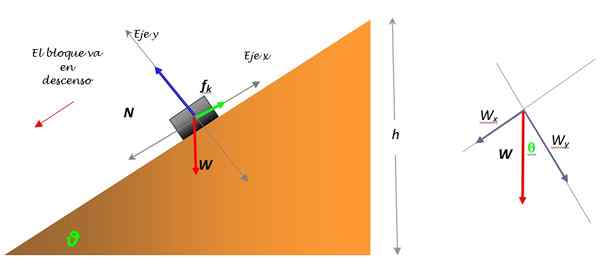Obrázok 5. Diagram knihy -bezplatný telesný diagram na naklonenej rovine a rozklad hmotnosti. Zdroj: Self Made.

Hmotnosť knihy má veľkosť W = mg, Je však potrebné ju rozdeliť na dve zložky: W_X a W_a, Pretože je to jediná sila, ktorá nespadá tesne nad žiadnu zo súradnicových osí. Rozklad hmotnosti sa pozoruje na obrázku vľavo.

W_a = mg.cosθ = 1.30 x 9.8 x cos 30 ° n = 11.03 n

W_X = mg.Senátor = 1.30 x 9.8 x sen 30 ° = 6.37 n

Druhý. Newtonov zákon pre vertikálnu os je:

N - wy = 0

N = mg. cos θ = 11.03 n.

Aplikácia 2. Newtonov zákon pre os x, ktorý si vybral ako pozitívny smer možného pohybu:

W_X - F_siež = 0

Maximálne trenie je F_{siež maximálny}= μ_siežN, preto:

W_X - μ_siežN = 0

μ_siež = W_X / N = 6.37/11.03 = 0.58

Odkazy

1. Rex, a. 2011. Základy fyziky. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7^mamička. Edimatizovať. Učenie sa. 120 - 124.
3. Serway, r., Vulle, C. 2011. Základy fyziky. 9^nat Edimatizovať. Učenie sa. 99-112.
4. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. Kopec MacGraw. 71 - 87.
5. Walker, J. 2010. Fyzika. Addison Wesley. 148-164.