Pozoruhodné výrobky

Čo sú pozoruhodné výrobky?

Pozoruhodné výrobky sú algebraické operácie, kde sa vyjadrujú násobky polynómov, ktoré nemusia byť tradične vyriešené, ale s pomocou určitých pravidiel sa ich výsledky objavia.

Polynómy sa vynásobia tým, či je preto možné, že majú veľa výrazov a premenných. Aby sa tento proces skrátil, používajú sa pravidlá významných výrobkov, ktoré umožňujú násobenie bez toho, aby museli ísť na termín na termín.

Pozoruhodné výrobky a príklady

Každý pozoruhodný produkt je vzorec, ktorý je výsledkom faktorizácie, zložený z polynómov niekoľkých pojmov, ako sú binomiály alebo trinomialy, nazývané faktory.

Faktory sú základom moci a majú exponent. Ak sa faktory vynásobia, musia sa pridať exponenty.

Existuje niekoľko pozoruhodných vzorcov produktu, niektoré sa používajú viac ako iné, v závislosti od polynómov a sú nasledujúce:

Štvorcový binomický

Je to násobenie binomialu samo osebe, vyjadrené vo forme moci, kde sa výrazy pridávajú alebo odpočítajú:

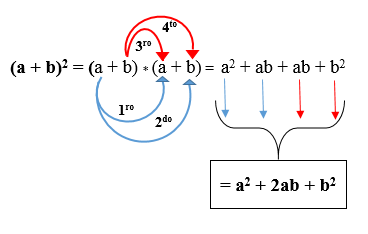
do. Binomický sumy štvorcový: Rovná sa s štvorcom prvého termínu a zdvojnásobí produkt pojmov plus štvorec druhého funkčného obdobia. Vyjadruje sa takto:

(A + b)² = (a + b) _* (A + b).

Na nasledujúcom obrázku vidíte, ako sa produkt vyvíja podľa vyššie uvedeného pravidla. Výsledok sa nazýva Trinomial of Perfect Square.

Príklad 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Príklad 2

(4a + 2b) = (4a)² + 2 (4 _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

b. Binomén štvorcového odčítania: Rovnaké pravidlo binomialu sumy sa uplatňuje, iba to, že v tomto prípade je druhý funkčný čas negatívny. Jeho vzorec je nasledujúci:

(A - b)² = [(a) + (- b)]²

Môže vám slúžiť: numerické analógie: typy, aplikácie a cvičenia

(A - b)² = a² +Druhý _* (-B) + (-B)²

(A - b)²   = a² - 2ab + b².

Príklad 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Konjugát Binomials Product

Dva binomiály sa konjugujú, keď sú druhé výrazy každého z nich rôzne príznaky, to znamená, že prvé je pozitívne a druhé negatívne alebo naopak. Je vyriešený zdvihnutím každého monomického štvorca a odpočítaný. Jeho vzorec je nasledujúci:

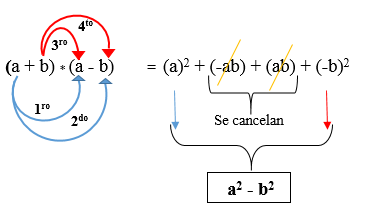
(A + b) _* (A - b)

Na nasledujúcom obrázku sa vyvíja produkt dvoch konjugovaných binomiálov, kde sa pozoruje, že výsledkom je rozdiel štvorcov.

Príklad 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 AB) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

Produkt dvoch binomiálov so spoločným pojmom

Je to jeden z najkomplexnejších a málo používaných významných produktov, pretože je to násobenie dvoch binomiálov, ktoré majú spoločný termín. Pravidlo označuje nasledujúce:

• Štvorec spoločného pojmu.
• Plus súčet výrazov, ktoré nie sú bežné, a potom ich vynásobia spoločným pojmom.
• Plus súčet násobenia podmienok, ktoré nie sú bežné.

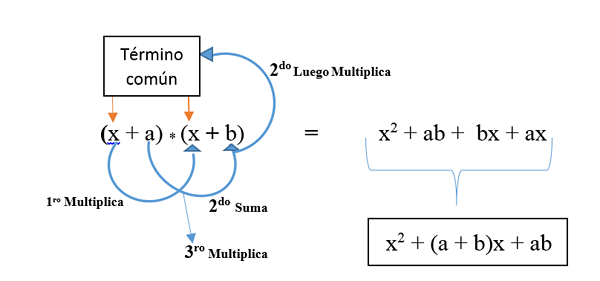
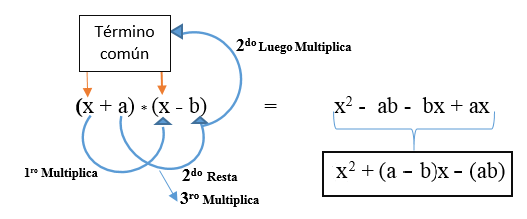
Je zastúpený vo vzorci: (x + a) _* (x + b) a je vyvinutý, ako je to znázornené na obrázku. Výsledkom je nekonečný štvorcový trinomiál.

Príklad 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Existuje možnosť, že druhý termín (iný termín) je negatívny a jeho vzorec je nasledujúci: (x + a) _* (x - b).

Príklad 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Môže sa tiež stať, že oba rôzne výrazy sú negatívne. Váš vzorec bude: (x - a) _* (x - b).

Môže vám slúžiť: Lamy veta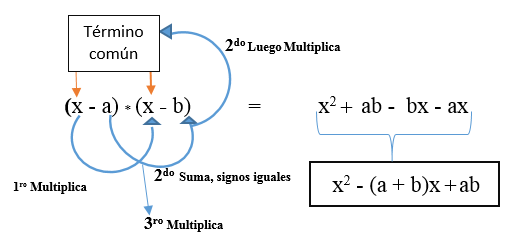

Príklad 3

(3B - 6) _* (3B - 5) = (3B _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3B - 6) _* (3b - 5) = 9b² + (-eleven) _* (3b) + (30)

(3B - 6) _* (3b - 5) = 9b² - 33b + 30.

Štvorcový polynóm

V tomto prípade existujú viac ako dva termíny a na jeho rozvoj je každý z nich rezaný a pridáva spolu s dvojnásobkom násobenia jedného termínu s druhým; Jeho vzorec je: (a + b + c)² A výsledkom operácie je trinomický štvorcový.

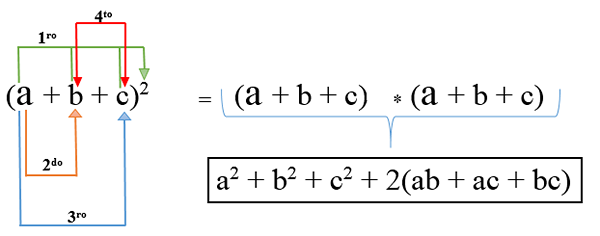
Príklad 1

(3x + 2y + 4z)² = (3x)² + (2 a)² + (4z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16z² + 12xy + 24xz + 16yz.

Binomický kocka

Je to komplexný významný produkt. Na jeho rozvoj je binomiál znásobený jej štvorcom takto:

do. Pre binomický k kocke sumy:

• Prvá kocka a trojnásobok štvorca prvého funkčného obdobia druhým.
• Plus trojnásobok prvého funkčného obdobia, od druhého štvorca.
• Plus kocka druhého funkčného obdobia.

(A + b)³ = (a + b) _* (A + b)²

(A + b)³ = (a + b) _* (² + 2ab + b²)

(A + b)³ = a³ + Druhý²B + AB² + BA² + 2Ab² + b³

(A + b)³ = a³ + Tretí²B + 3ab² + b³.

Príklad 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

b. Pre binomiálny do kocky odčítania:

• Kocka prvého funkčného obdobia, s výnimkou trojitého štvorca prvého funkčného obdobia druhým.
• Plus trojnásobok prvého funkčného obdobia, od druhého štvorca.
• Menej kocka druhého funkčného obdobia.

(A - b)³ = (a - b) _* (A - b)²

(A - b)³ = (a - b) _* (² - 2ab + b²)

(A - b)³ = a³ - Druhý²B + AB² - BA² + 2Ab² - b³

(A - b)³ = do³ - Tretí²B + 3ab² - b³.

Príklad 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Môže vám slúžiť: NEPRAVENÉ ÚDAJE: Príklady a vyriešené cvičenie

(B - 5)³ = b³ - 15b² +75b - 125.

Trinomická kocka

Vyvíja ho znásobením jej štvorcom. Je to veľmi rozsiahly pozoruhodný produkt, pretože na kocke sa zvyšujú 3 výrazy, plus trojnásobok každého pojmu s štvorcom, vynásobený každým z podmienok plus šesťnásobok produktu týchto troch výrazov. Videné v lepšej podobe:

(A + b + c)³ = (A + b + c) _* (A + b + c)²

(A + b + c)³ = (A + b + c) _* (² + b² + c² + 2AB + 2AC + 2BC)

(A + b + c)³ = A³ + b³ + c³ + Tretí²B + 3ab² + Tretí²C + 3AC² + 3B²C + 3BC² + 6ABC.

Príklad 1

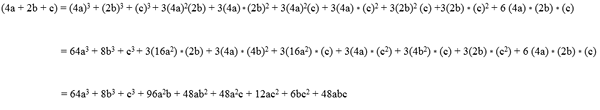
Vyriešené cvičenia pozoruhodných výrobkov

Cvičenie 1

Rozvíjajte nasledujúci binomický do kocky: (4x - 6)³.

Riešenie

Pamätajte si, že binomiál pre kocku sa rovná prvému funkčnému obdobiu zvýšeného na kocku, s výnimkou trojitého štvorca prvého funkčného obdobia druhého; plus trojnásobok prvého funkčného obdobia, druhým štvorcom, s výnimkou kocky druhého funkčného obdobia.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Cvičenie 2

Vyvíjajte nasledujúci binomický: (x + 3) (x + 8).

Riešenie

Máte binomický, kde existuje spoločný termín, ktorý je x a druhý termín je pozitívny. Na jeho rozvoj sa musí zvýšiť iba spoločný termín, plus súčet výrazov, ktoré nie sú bežné (3 a 8), a potom ich vynásobte spoločným pojmom, plus súčet násobenia podmienok, ktoré nie sú bežné.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Odkazy

1. Anjel, a. R. (2007). Elementárna algebra. Pearson Vzdelanie,.
2. Arthur Goodman, L. H. (Devätnásť deväťdesiat šiestich). Algebra a trigonometria s analytickou geometriou. Pearson Vzdelanie.
3. Das, s. (s.F.). Matematika plus 8. Spojené kráľovstvo: Sagar Ratna.
4. Jerome e. Kaufmann, K. L. (2011). Elementárna a stredná algebra: kombinovaný prístup. Florida: Cengage Learning.
5. Pérez, C. D. (2010). Pearson Vzdelanie.