Pentagonálne charakteristiky hranolu, časti, vrcholy, okraje, objem

A Pentagonálny hranol Je to trojrozmerná geometrická postava, ktorej základne majú identický tvar Pentagonu a má tiež celkom 5 -rémy vo forme rovnobežníka.

Ak sú tváre obdĺžnikové, hovorí sa, že je to Priamy pentagonálny hranol, Zatiaľ čo ak sú okraje naklonené základom, potom je to a šikmý pentagonálny hranol. Na nasledujúcom obrázku je príklad každého z nich.

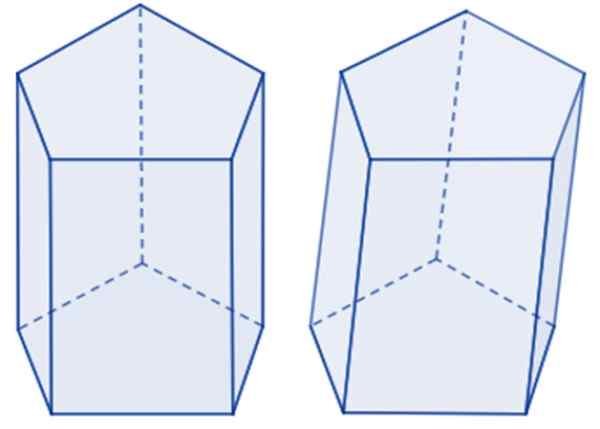Pentagonálny hranol vľavo a šikmé doprava. Zdroj: Wikimedia Commons.

Základný pentagón môže byť pravidelný, ak jeho päť strán má rovnaké opatrenie, ako aj vnútorné uhly, inak je to nepravidelný Pentagon. Ak je základňa hranolu pravidelná, ide o pravidelný pentagonálny hranol. Inak je hranol nepravidelný pentagonálny.

Nepravidelné základné pentagonálne hranoly používané v modernej konštrukcii. Zdroj: Tapeta Flare.

Pentagonálny hranol je harmonická štruktúra, ktorá sa používa v architektúre a navrhovaní predmetov, ako je moderná budova znázornená na hornej časti postavy. Okná nepravidelného Pentagonu tvoria základňu hranolov.

[TOC]

Charakteristika pentagonálneho hranolu

-Je to trojrozmerná geometrická postava, povrchy, ktoré ho tvoria, obsahujú určitý objem.

-Ich základy sú pentagóny a ich bočné tváre môžu byť obdĺžniky alebo rovnobežníky.

-Má vrcholy -rohy Prisma -a okrajov -brehy alebo pobrežie-.

-Ak sú hrany, ktoré spájajú základne, kolmé, hranol je rovný a ak sú naklonené, hranol je šikmý.

-Ak je základňou pentagón, ktorého vnútorné uhly sú menšie ako 180 °, hranol je vypuklý, Ale ak je jeden alebo viac vnútorných uhlov väčší ako 180 °, je to hranol konkávny.

Priezvisko

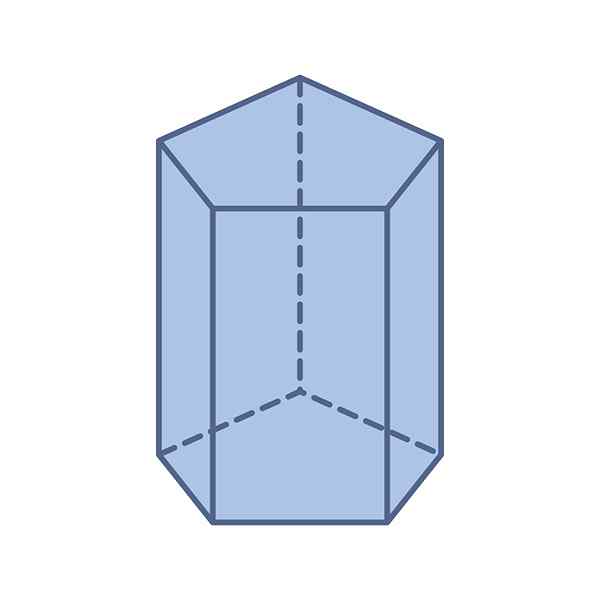
-Základne: Má dve pentagonálne a zhodné základne -jeho merania sú rovnaké -pravidelné alebo nepravidelné.

Môže vám slúžiť: Všeobecný vzorec: kvadratické rovnice, príklady, cvičenia

-Tváre: Pentagonálny hranol má celkom 7 tvárí: dve pentagonálne základne a päť rovnobežiek, ktoré tvoria strany.

-Hrana: segment, ktorý spája dve základne, zobrazené červenou farbou na obrázku 3 alebo v segmente, ktorý spája dve strany.

-Výška: Vzdialenosť medzi tvárami. Ak je hranol rovný, táto vzdialenosť sa zhoduje s veľkosťou okraja.

-Vrchol: Bežný bod medzi základňou a dvoma bočnými stranami.

Spodný obrázok ukazuje pravidelný základný pentagonálny hranol, v ktorom segmenty, ktoré tvoria základňu, majú rovnakú mieru nazývanú do.

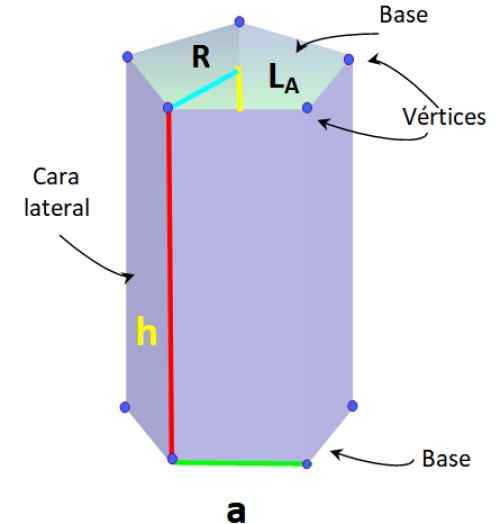 Pravidelné prvky pentagonálnych hranolov. Zdroj: f. Zapata.

Tento typ hranolu má tiež nasledujúce prvky, typické pre pravidelný Pentagon:

-Rádio r: Vzdialenosť medzi stredom Pentagonu a jedným z vrcholov.

-Apotheme l_Do: segment, ktorý sa spája s stredom jednej zo strán Pentagonu.

Koľko vrcholov má pentagonálny hranol?

V Pentagone je 5 vrcholov a ako Pentagonálny hranol má dva pentagóny ako základne, toto telo má celkom 10 vrcholov.

Koľko hrán má pentagonálny hranol?

Môžete vypočítať počet hrán pre geometrické telá s plochými tvárami, ako sú hranoly, pomocou Eulerova veta Pre konvexné polyhedros. Leonhard Euler (1707-1783) je jedným z najväčších matematikov a fyzických v histórii.

Veta vytvára vzťah medzi počtom tvárí, ktoré nazývame C, množstvo vrcholov V a celkové hrany a takto:

C+V = A+2

Pre pentagonálny hranol, ktorý máme: C = 7 a V = 10. Vymazanie, počet hrán:

Môže vám slúžiť: Bijjektívna funkcia: Čo je to, ako sa to robí, príklady, cvičenia

A = C+V-2

Výmena hodnôt:

A = 7 + 10 - 2 = 15

Pentagonálny hranol má 15 hrán.

Ako získať objem pentagonálneho hranolu?

Objem pentagonálneho hranolu meria priestor zamknutý bokmi a základňami. Je to kladná suma, ktorá sa vypočíta podľa nasledujúcej vlastnosti:

Akákoľvek rovina, ktorá sa znižuje na hranol kolmo na jej okraje, vytvára križovatku rovnakým spôsobom ako základňa, to znamená Pentagon rovnakých dimenzií.

Objem pentagonálneho hranolu je preto produktom základnej oblasti a výškou hranolu.

Byť Do_B Pentagonálna základná oblasť a h Výška hranolu, potom objem Vložka je:

V = a_B x h

Tento vzorec je všeobecný, je platný pre akýkoľvek hranol, pravidelný alebo nepravidelný, priamy alebo šikmý.

Objem hranolu je vždy dodávaný v jednotkách dĺžky vysoký do kocky. Ak sú dĺžka bokov a výška hranolu uvedené v metroch, potom je objem vyjadrený v m³, že „kubické metre“ sa čítajú. Medzi ďalšie jednotky patrí CM³, km³, palcov³ a viac.

- Pravidelný objem Pentagonal hranol

V Pentagonal Prism sú pravidelné základne pravidelné pentagóny, čo znamená, že strana a vnútorné uhly sú rovnaké. Vzhľadom na symetriu tela, Pentagonova oblasť, a preto sa objem ľahko vypočíta niekoľkými spôsobmi:

Poznanie výšky a merania strany

Byť do Miera pentagonálnej základnej strany. V takom prípade sa oblasť počíta:

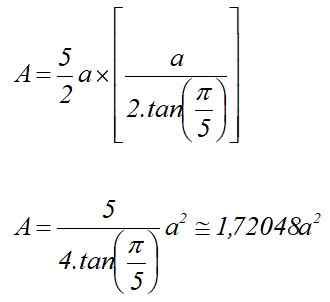
Preto objem pravidelného pentagonálneho hranolu výšky H je:

Môže vám slúžiť: imaginárne čísla: Vlastnosti, aplikácie, príklady

V = 1.72048 a²⋅ h

Poznať výšku a mieru rádiu

Keď Rádio r Z pentagonálnej základne sa táto ďalšia rovnica môže použiť pre základnú oblasť:

A = (5/2) r²⋅ Sen 72 °

Týmto spôsobom je objem pentagonálneho hranolu daný:

V = (5/2) r² ⋅ h ⋅ sen 72 °

Kde h Je to výška hranolu

Poznanie výšky, miery apotheme a obvodovej hodnoty

Pentagonálna základná plocha sa dá vypočítať, ak je známy jeho obvod P, čo je jednoducho súčet strán, ako aj miera apothémie l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l l_Do:

A = p. L_Do / 2

Vynásobenie tohto výrazu hodnotou výšky h, Máme objem hranolu:

V = P. L_Do .H / 2

- Nepravidelný objem hranolu Pentagonal

Vzorec uvedený na začiatku je dokonca platný, keď základom hranolu je nepravidelný Pentagon:

V = a_B x h

Na výpočet základnej oblasti sa používajú napríklad rôzne metódy:

-Metóda triangulácie, ktorá pozostáva z rozdelenia Pentagonu na trojuholníky a štvoruholníky, ktorých príslušné oblasti sa ľahko vypočítajú. Oblasť Pentagon bude súčet oblastí týchto jednoduchších čísel.

-Gauss Determinants Method, pre ktorú musíte poznať vrcholy obrázku.

Po určení hodnoty oblasti sa vynásobí výškou hranolu, aby sa získal objem.

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Matematika otvorená referencia. Polygón. Získané z: Mathpenref.com.
3. Vesmír. Eulerova veta pre polyhedros. Získané z: Universoformulas.com.
4. Vesmír. Oblasť pravidelného Pentagonu. Získané z: Universoformulas.com.
5. Wikipedia. Hranol. Obnovené z: je.Wikipedia.com.
6. Wikipedia. Pentagonálny hranol. Obnovené z: je.Wikipedia.com.