Heptagonálny hranol
- 2604
- 412
- Gabriel Bahna
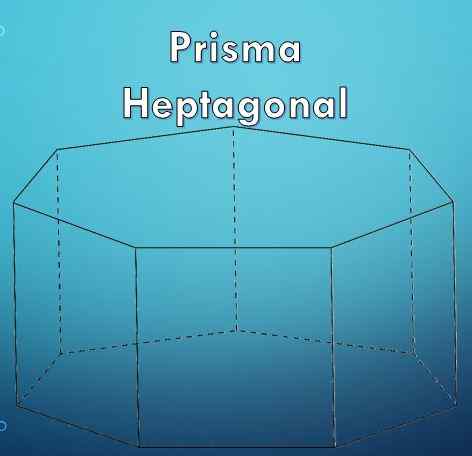
 Heptagonálny hranol má 7 strán
Heptagonálny hranol má 7 strán Čo je heptagonálny hranol?
A heptagonálny hranol Je to geometrické číslo, ktoré, ako už názov napovedá, zahŕňa dve geometrické definície, ktoré sú: hranol a heptagon. „Prism“ je obmedzená geometrická postava o dve bázy, ktoré sú rovnaké a rovnobežné polygóny a ich bočné tváre sú rovnobežníky.
„Heptagon“ je polygón, ktorý tvorí sedem (7) strán. Pretože heptagón je polygón, môže byť pravidelný alebo nepravidelný.
Polygón sa hovorí, že je pravidelný, ak majú všetky ich strany rovnakú dĺžku a ich vnútorné uhly sa merajú rovnako, nazývajú sa tiež rovnostranné polygóny; Inak sa hovorí, že polygón je nepravidelný.

Charakteristiky heptagonálneho hranolu
Nižšie sú uvedené určité vlastnosti, ktoré majú heptagonálny hranol, ako napríklad: jeho konštrukcia, vlastnosti jeho základne, oblasť všetkých jeho tvárí a objem.
1- výstavba
Na vybudovanie heptagonálneho hranolu sú potrebné dva heptagóny, ktoré budú jeho základmi a sedem rovnobežní, jeden na každej strane heptagónu.
Začne kresliť heptagón, potom je nakreslených sedem zvislých čiar, z rovnakej dĺžky, ktoré opúšťajú z každého z jeho vrcholov.
Nakoniec je nakreslený ďalší heptagon, že jeho vrcholy sa zhodujú s koncom čiary nakreslených v predchádzajúcom kroku.
Heptagonálny hranol, ktorý sa predtým nakreslil, sa nazýva priamy heptagonálny hranol. Ale môžete mať tiež šikmú heptagonálnu hranol, ako je nasledujúca postava.
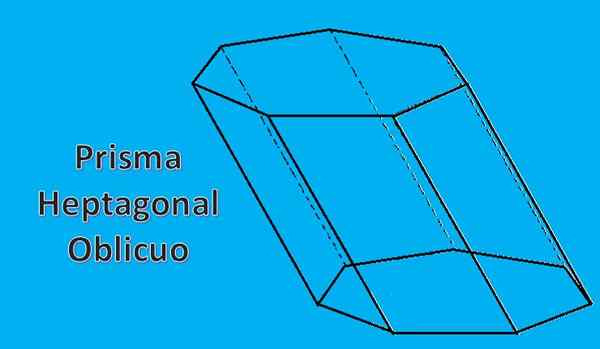
2- vlastnosti jeho základne
Pretože ich základne sú heptogóny, spĺňajú, že diagonálne číslo je d = nx (n-3)/2, kde „n“ je počet strán mnohouholníka; V takom prípade musíte d = 7 × 4/2 = 14.
Môže vám slúžiť: Aké sú trojuholníkové čísla? Vlastnosti a demonštrácieVidíme tiež, že súčet vnútorných uhlov akéhokoľvek heptagónu (pravidelného alebo nepravidelného) je rovnaký 900 °. Toto je možné skontrolovať podľa nasledujúceho obrázka.
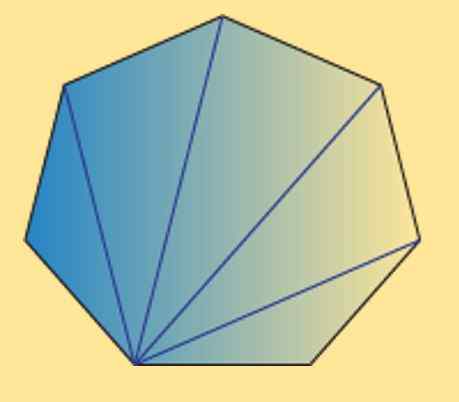
Ako je vidieť, existuje 5 vnútorných trojuholníkov a pomocou toho, že súčet vnútorných uhlov trojuholníka sa rovná 180 °, je možné získať, že požadovaný výsledok.
3- oblasť potrebná na vybudovanie heptagonálneho hranolu
Pretože jeho základne sú dva heptogóny a jeho strany sú sedem rovnobežní, oblasť potrebná na vybudovanie heptagonálneho hranol rovnobežník.

V tomto prípade bude vypočítaná oblasť pravidelného heptagónu. Z tohto dôvodu je dôležité poznať definíciu apothémie.
Apotheme je kolmá čiara, ktorá prechádza zo stredu pravidelného polygónu do stredu ktorejkoľvek z jeho strán.
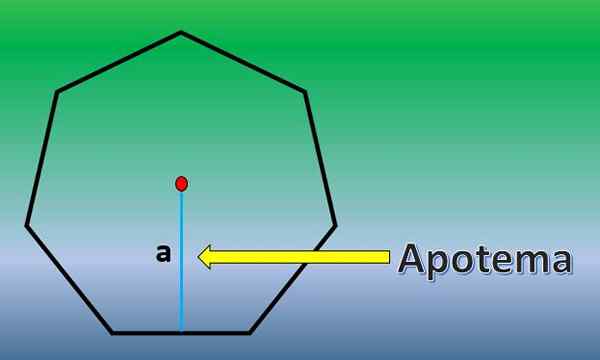
Akonáhle je apotheme známy, plocha heptagonu je h = 7xlxa/2, kde „L“ je dĺžka každej strany a „A“ dĺžka apotheme.
Plocha rovnobežníka sa dá ľahko vypočítať, je definovaná ako p = lxh, kde „L“ je rovnaká dĺžka strany heptagónu a „H“ je výška hranolu.
Záverom je, že množstvo materiálu potrebného na vybudovanie heptagonálneho hranolu (s bežnými základňami) je 7xlxa+7xlxh, tj 7xl (a+h).
4- objem
Akonáhle je plocha bázy a výška hranolu známa, objem je definovaný ako (základná plocha) x (výška).
V prípade heptagonálneho hranolu (s pravidelnou základňou) musí byť V = 7xlxaxh/2; Môže byť tiež napísaný ako v = pxaxh/2, kde „p“ je obvodom bežného heptagónu.
Môže vám slúžiť: aké sú delení z 30? (Vysvetlenie)- « Bolo to pred tým, čo je, história, charakteristiky
- V ktorých subjekty sú viac nemetalických minerálov? »

