Fyzický

Zásada prenosnosť síl

Zásada prenosnosť síl

Vysvetlíme, čo je zásada prenosu, s vyriešenými príkladmi a cvičeniami

Aký je zásada prenosu?

On Zásada prenosu Vzťahuje sa na pevné predmety a potvrdzuje, že aplikovaná sila na určitý bod tela je rovnocenná s inou silou rovnakej veľkosti a smeru, pokiaľ je uvedená sila aplikovaná na rovnakú čiaru, ktorá obsahuje pôvodnú silu.

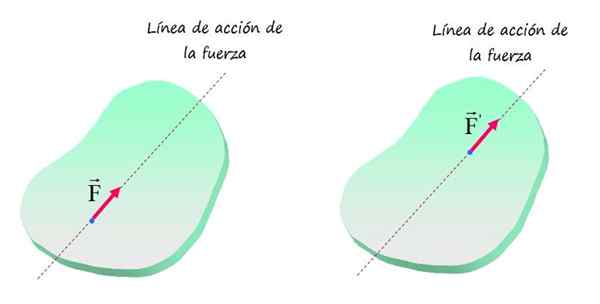
Preto akákoľvek sila rovnakej veľkosti a smeru spôsobí rovnaký účinok translačného a rotačného pohybu na objekt, za predpokladu, že jeho aplikačný bod je umiestnený na rovnakom riadku, ako je znázornené na nasledujúcom obrázku.

V rigidnom tele sa účinok sily nemení, keď sa jeho aplikácia pohybuje pozdĺž svojej činnosti. Zdroj: f. Zapata.

Zobrazené sily F a F„Hovorí sa, že sú rovnocenné sily a náhla priamka, ktorá ich obsahuje, sa volá Vynútiť akčnú líniu.

Princíp prenosu je veľmi užitočný, pretože umožňuje pohodlie síl, ktoré pôsobia na objekt, s cieľom uľahčiť analýzu.

Vysvetlenie Zásada prenosu

Princíp prenosu je založený na skutočnosti, že dve sily F1 a F2 Sú rovnocenní, pod podmienkou, že majú rovnakú veľkosť a rovnaký smer.

Okrem toho musia produkovať rovnaký okamih v súvislosti s akýmkoľvek bodom alebo, čo je zaručené rovnakou činnosťou a pretože moment je produktom sily podľa vzdialenosti alebo do uvedenej čiary.

Všimnite si, že princíp sa vzťahuje iba na tuhé telo, to znamená objekt, v ktorom sa relatívne vzdialenosti medzi ich časťami nemenia, pretože vnútorné sily, ktoré ho udržiavajú v súdržnosti, sú dostatočne intenzívne. Preto objekt nemení svoju formu, či už na ňom tieto vonkajšie sily konajú alebo nie.

Na druhej strane, ak objekt nie je rigidný, úpravy bodu uplatňovania síl by spôsobilo variácie, pokiaľ ide o napätie alebo kompresiu aplikované na telo, čo by viedlo k zmenám vo svojej forme.

Predpokladajme, že telo je tuhé, nie je nič iné ako idealizácia, pretože v skutočnosti sú všetky objekty deformovateľné vo väčšej alebo menšej miere. V mnohých prípadoch je to však vynikajúci prístup, ak je deformácia dostatočne malá na to, aby bola považovaná.

Obmedzenia

Princíp prenosu má, ako je uvedené, obmedzenie, pokiaľ ide o vnútorné účinky streľby alebo posunutia síl. Na nasledujúcom obrázku je znázornený objekt so silami F a F„Aplikuje sa v rôznych bodoch tej istej činnosti.

Môže vám slúžiť: Princíp Archimedes: vzorec, demonštrácia, aplikácie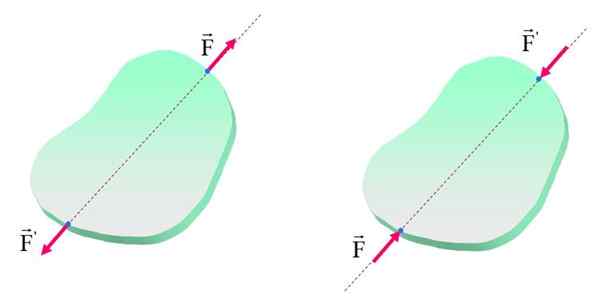Princíp prenosu je uplatniteľný iba v tuhých telách, pretože úprava bodu uplatňovania síl môže mať rôzne účinky na deformovateľné orgány. Zdroj: f. Zapata.

Všimnite si, že na oboch obrázkoch je telo (pevné alebo nie) v rovnováhe, pretože sily majú rovnakú veľkosť a smer a opačné zmysly. Okrem toho sú sily, ako už bolo povedané, na rovnakej línii konania, ale na ľavej strane je účinok na telo napätie, zatiaľ čo vpravo je kompresia kompresia.

Preto, aj keď telo zostáva v pokoji, vnútorné účinky sú rôzne a stávajú sa patentovaním, ak objekt nie je úplne rigidný. V prípade ľavice majú sily tendenciu rozširovať telo, zatiaľ čo napravo majú tendenciu ho skrátiť.

Príklady Zásada prenosu

Príklad 1

Predpokladajme, že máte na horizontálnej podlahe ťažký kmeň. Účinok tlačenia na ľavú stranu je rovnaký, ako keby bol plochý. V tomto prípade je pohyb kufra na zemi rovnaký.

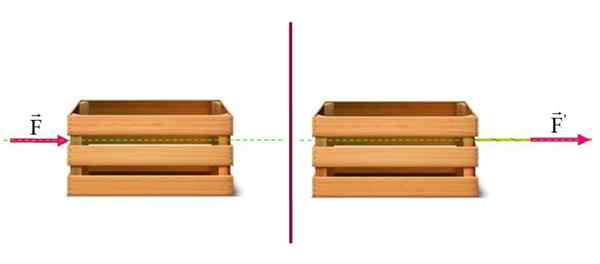Účinok tlačenia alebo ťahania zásuvky na horizontálny povrch je rovnaký: posuňte ju zľava doprava. Zdroj: f. Zapata.

Príklad 2

Máte dlhú dosku ako polica. Na jeho inštaláciu je to ekvivalent.

V obidvoch prípadoch budú mať sily, ktoré vyvážia dosku.

Princíp prenosu a momenty

Predpokladajme, že v bode A sa aplikuje sila F, v okamihu, keď vzniká táto sila okolo bodu alebo je znázornená na obrázku, je:

MAni = rDo × F

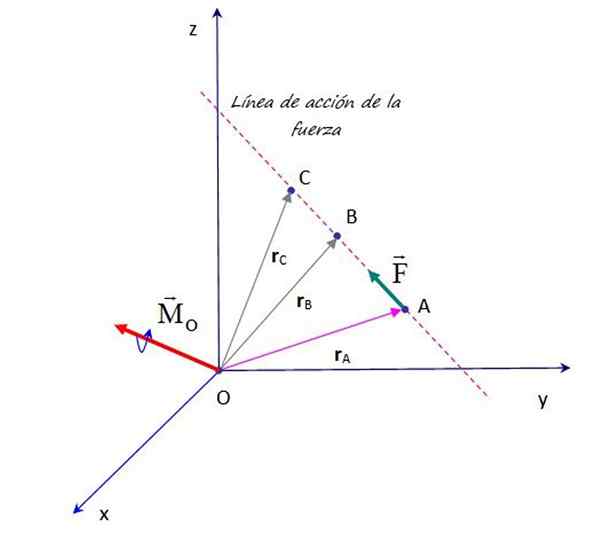Posuňte alebo prenosovú silu pozdĺž svojej línie akcie neupravuje okamih, v ktorom sa uplatňuje na bod alebo. Zdroj: f. Zapata.

Zásada prenosu zaisťuje, že to zaisťuje F, konanie v akomkoľvek bode v rámci svojej línie akcie, napríklad body B, C a ďalšie, pochádza z rovnakého okamihu vzhľadom na bod alebo. Preto je platné potvrdiť, že:

MAni = rDo × F  = rB × F = rC × F

Vyriešené cvičenia

Cvičenie 1

Homogénna guľa má hmotnosť m = 5 kg a spočíva na vodorovnom povrchu bez trenia.

    • a) Nakreslite schému Sila, ktorá vyvíja povrch na gule.
    • b) Vytvorte voľný diagram tela gule
    • c) Vypočítajte hodnotu normálnej sily vyvíjanej povrchom na gule.

  • Riešenia A a B

V grafe a) sila vyvíjaná povrchom na gule je znázornená, nazývaná normálna N, Pretože je kolmá na povrch. Bod uplatňovania sily sa zhoduje s podporným bodom gule na povrchu (bod v zelenom) a línia pôsobenia je zvislá, ktorá prechádza geometrickým stredom gule.

Môže vám slúžiť: Zemská magnetosféra: Charakteristiky, štruktúra, plyny

V grafe b) je diagram voľného tela gule, kde je okrem normálnej hmotnosti znázornená, ktorá sa aplikuje v strede gravitácie, označená žltým bodom.

Vďaka princípu prenosu, normálnej sily N Môže sa preniesť do tohto bodu bez zmeny jeho účinkov na guľu. Tieto účinky nie sú ďalšie, ktoré udržiavajú sféru podporovanú na stole v rovnováhe.

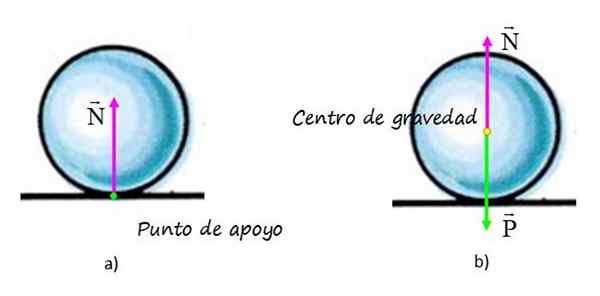Na obrázku A) vľavo normálne pôsobí na podporný bod gule s povrchom. Na obrázku B), na diagrame voľného tela sa normálny prenáša do stredu gravitácie, pretože vertikálna je jeho konanie. Jeho účinky nie sú upravené, pretože vyvažuje váhu tak, aby bola guľa v rovnováhe. Zdroj: f. Zapata.

  • Riešenie c

Keďže je guľa v rovnováhe, ako pozitívny zmysel vertikálny a negatívny vertikálny nadol, Newtonov druhý zákon vedie k:

N - p = 0

To znamená, že hmotnosť a normálne sú vyvážené, preto sú rovnaké v rozsahu:

N = p = mg = 5 kg × 9.8 m/s2 = 49 N, nasmerované vertikálne nahor.

Cvičenie 2

Uveďte, či je v nasledujúcich prípadoch splnený zásada prenosu:

  • Prvé puzdro

Sila 20 N vodorovne aplikovaná na tuhé telo je nahradená inou silou 15 N aplikovanou v inom bode na tele, hoci obe sa uplatňujú rovnakým smerom.

    • Riešenie

V tomto prípade sa princíp prenosu nebude splnený, hoci sa tieto dve sily uplatňujú rovnakým smerom, druhá sila nemá rovnakú veľkosť ako prvá. Preto nie je uvedený jeden z nevyhnutných podmienok zásady prenosu.

  • Druhý prípad

Sila 20 N vodorovne aplikovaná na tuhé telo je nahradená ďalším z 20 N, aplikovaná v inom bode tela a vertikálne.

    • Riešenie
Môže vám slúžiť: Planck Constant: vzorce, hodnoty a cvičenia

Pri tejto príležitosti nie je princíp prenosu splnený odvtedy, hoci tieto dve sily majú rovnaký modul, neuplatňujú sa rovnakým smerom. Opäť platí, že jedna z nevyhnutných podmienok zásady prenosu nie je uvedená. Dá sa povedať, že tieto dve sily sú rovnocenné.

  • Tretí prípad

Sila 10 N sa mení vodorovne na tuhom tele, tiež sa aplikuje aj na iný bod tela, ale rovnakým smerom a významom.

    • Riešenie

V tomto prípade je splnený princíp prenosu, pretože tieto dve sily majú rovnakú veľkosť a používajú sa rovnakým smerom a významom. Sú splnené všetky potrebné podmienky zásady prenosu. Dá sa povedať, že tieto dve sily sú rovnocenné.

  • Štvrtý prípad

Sila sa posúva smerom k vašej akčnej čiare.

    • Riešenie

V tomto prípade je princíp prenosu splnený, pretože, keďže je rovnaká sila, sa veľkosť aplikovanej sily nemení a vkĺzne do svojej akčnej čiary. Opäť sú splnené všetky potrebné podmienky zásady prenosu.

Cvičenie 3

Na pevnom tele sa uplatňujú dve vonkajšie sily. Obe sily sa aplikujú rovnakým smerom a rovnakým smerom. Ak je prvý modul 15 N a druhý z 25 N, aké podmienky by mali mať tretiu vonkajšiu silu, ktorá nahradí výsledok predchádzajúcich dvoch, aby splnila zásadu prenosu?

  • Riešenie

Na jednej strane musí byť hodnota výslednej sily 40 N, čo je výsledkom pridania modulu týchto dvoch síl.

Na druhej strane, výsledná sila musí konať kdekoľvek v priamke, ktorá sa spája s týmito dvoma bodmi uplatňovania týchto dvoch síl.

Odkazy

  1. Bedford, 2000. Do. Mechanika pre inžinierstvo: statické. Addison Wesley. 
  2. Pivo, f. 2010. Vektorová mechanika pre inžinierov. McGraw Hill. 5. Vydanie.
  3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
  4. Hibbeler, R. 2004. Inžinierska mechanika: statika. Sála.
  5. Meriam, J.L. 2012. Inžinierska mechanika: statika. 7. vydanie. Wiley & Sons.