Fyzický

Relatívny vzorec tlaku, ako sa vypočíta, príklady, cvičenie

Relatívny vzorec tlaku, ako sa vypočíta, príklady, cvičenie

Ten Presirelatívny To sa meria s ohľadom na určitú hodnotu alebo Odhalenie, čo je zvyčajne atmosférický tlak na hladine mora (štandardný atmosférický tlak). Je to vhodné, pretože veľká časť merania tlaku sa vykonáva pod plynnými vrstvami, ktoré tvoria atmosféru, ktorá vyvíja svoj vlastný tlak.

Na druhej strane sa meria absolútny tlak vzhľadom na celkové vákuum, v ktorom neexistujú žiadne molekuly interakcie. V nádobe, v ktorom bolo vyrábané vákuum, neexistujú žiadne častice, ktoré z vnútornej strany na stenách alebo na objektoch v ňom.

postava 1. Na meranie relatívneho tlaku sa používa tlakom. Zdroj: Wikimedia Commons.

Merané tlaky môžu byť nad alebo pod atmosférickým tlakom. V prvom prípade sa hovorí o tlak A v druhom z vákuový tlak.

Normálne tlaky, ktoré sa merajú denne v pneumatikách a krvnom tlaku, sú relatívnymi tlakmi, zatiaľ čo keď sa atmosférický tlak meria barometrom, je to absolútny tlak.

[TOC]

Relatívna tlaková vzorca

Relatívny tlak je rozdiel medzi absolútnym tlakom pAbsencia a atmosférický tlak PBankomat, Je to diferenciálny tlak alebo rozdiel v tlakoch. Pri relatívnom tlaku PZlyhať Je známy v angličtine ako Tlak Pg A je to dané vzťahom:

PAbsencia = PBankomat + Pg

PZlyhať = PAbsencia - PBankomat

Na tlak sa Pascal používa ako jednotka miery medzinárodného systému jednotiek, bez ohľadu na to, či ide o absolútny tlak alebo relatívny tlak.

Pascal je rovnocenný s silou vyvíjanou 1 Newtonom na ploche 1 m2, Ale iné jednotky sa často používajú, ako napríklad ortuť, voda, anglo -saxonové jednotky, ako napríklad psi a ďalšie.

Môže vám slúžiť: 31 typov sily vo fyzike a ich charakteristiky

Ako sa vypočíta relatívny tlak?

Ak je absolútny tlak známy v jednom bode a štandardnom atmosférickom tlaku, relatívny tlak je odčítanie medzi oboma.

Napríklad predpokladajme, že absolútny tlak v určitom systéme je 305 kPa. S vedomím, že štandardný atmosférický tlak je 101.3 kPa, relatívny tlak je:

Pg = PAbsencia - PBankomat = 305 - 101.3 kPa = 203.7 kPa

KPA alebo Kilopascal je tisíckrát väčší ako Pascal. Používa sa častejšie, pretože hodnoty tlaku sú v poradí tisícov Pascal. Hmotnosť jablka je približne 1 Newton a Pascia je rovnocenná s touto silou distribuovanou na 1 metrovom bočnom štvorci. Iné násobky, ako napríklad Megapascal (1 MPa = 1 x 106 Pa) alebo Gigapascal (1 GPA = 1x 109 Pa).

Tlak príkladu je manometrický, pretože je nad atmosférickým tlakom, ale pod týmto sú absolútne tlaky. Napríklad, ak má plyn v nádobe absolútny tlak 50 kPa, jeho relatívny tlak je vákuový tlak, ktorý vytvára sacie:

Pg = PAbsencia - PBankomat = 50 - 101.3 kPa = -51.3 kPa

V týchto príkladoch sa použil štandardný atmosférický tlak, čo je tlak na hladine mora. Ak sa však pri výpočte vyžaduje väčšia presnosť, môže sa použiť lokálny atmosférický tlak, ktorý sa môže líšiť od 101.3 kPa, pretože závisí od nadmorskej výšky a iných geografických podmienok.

V textoch sú zvyčajne uvedené tlaky relatívne, a ak je potrebné pracovať s absolútnymi tlakmi, tieto sa rozlišujú s použitím predplatných, aby sa predišlo zámene.

Môže ti slúžiť: slnko

Variácia tlaku s hĺbkou

V každom bode vo vnútri tekutiny, ako je voda, je tlak. Za predpokladu, že voda je nestlačiteľná, takže jej hustota zostáva konštantná a tlak sa mení vertikálne.

Môže sa skontrolovať tým, že vezme malú časť tekutiny vo forme hrubého disku D Y to je v pokoji uprostred tekutej hmotnosti.

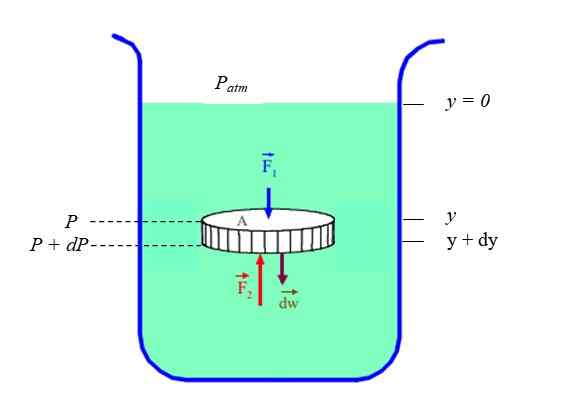Obrázok 2. Malá časť tekutiny tvare diskov, v statickej rovnováhe. Zdroj: f. Zapata.

Sily na kruhových okrajoch disku sú rušivé, ale nie sily vyvíjané hmotnosťou tekutiny nad a pod diskom: F1 a F2. Okrem toho je potrebné brať do úvahy hmotnosť tekutého diskuW V Newtonovom druhom zákone:

∑fa = F2 - F1 - W = 0

Tieto sily môžu byť vyjadrené z hľadiska tlaku, ktorý je kolmou silou na jednotku plochy. Týmto spôsobom máme tlak P, ktorý je vytvorený silou f1:

F1 = P. Do

Kde a je kruhová plocha disku. Podobne:

F2 = (P + dp). Do

S p + dp tlak v hĺbke a + dy. Hmotnosť je dw = dm . G:

(P + dp). A - P. A - DM . G = 0

Hustota tekutiny je ρ = dm/ dv, s DV objemom tekutého disku, daný a.D Y. Tadiaľto:

(P + dp). A - P. A - ρa.D Y .G = 0

Získaná rovnica sa zjednodušila na:

Dp - ρgdy = 0 → dp = ρgdy

Integrácia oboch strán z a1 až Y2:

= P2 - P1 = ρg (a2 - a1)

Termín P2 - P1 Je to rozdiel v tlakoch alebo diferenciálnom tlaku. Ak chceme poznať tlak vo vertikálnom súradnicovom bode a, áno a1 = 0, a2 = y a Pani = PBankomat. S tým budeme mať tlak vo vzťahu k tejto hĺbke, ktorá závisí výlučne od hĺbky a:

Môže vám slúžiť: Nepravidelná galaxia: Tvorba, charakteristiky, typy, príklady

P2 - PBankomat = ρgy ⇒ PZlyhať = ρgy

Príklady relatívneho tlaku

Tlak na spodnej časti bazénu

Všetci sme zažili tlak, ktorý pociťuje ponorením sa do bazéna alebo do mora. Aký je relatívny tlak, ktorý pociťuje ponorením sa do bazénu sladkej vody na 5 metrov hlboký? Pomocou predchádzajúceho výrazu a s vedomím, že hustota sladkej vody je 1000 kg/m3, S g = 9.81 m/s2 Relatívny tlak je:

PZlyhať = ρgy = 1 000 x 9.81 x 5 pa = 49050 PA.

Tlak na pneumatiku

Pneumatiky vozidla sú zvyčajne na tlaku 32 psi. Toto je relatívny alebo manometrický tlak v librách na štvorcový palec, jednotka používaná v anglických krajinách. V týchto jednotkách je kalibrovaných veľa manometrov. 32 psi sa rovná 220632 Pa o 220 kPa.

Cvičenie

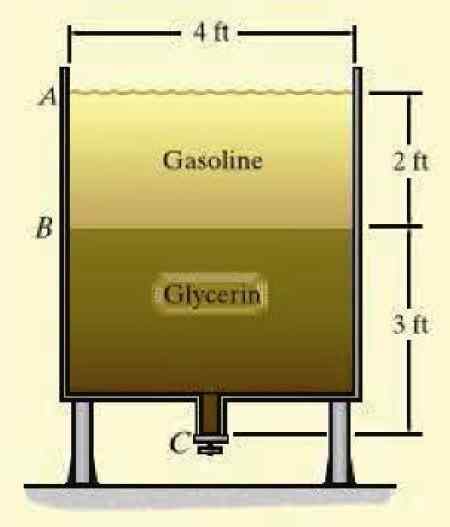
Tank obsahuje benzín a glycerín, dve neisiteľné kvapaliny (nemiešajte) v uvedených výškach. Aký je manometrický tlak na spodnej časti nádrže? Konkrétne hmotnosti sú pripojené, označené gréckym písmenom γ z každej tekutiny:

γplyn = 45.3 lb/ft3

γGly = 78.7 lb/ft3

Obrázok 3. Tank plný s dvoma neobyčajnými tekutinami. Zdroj: Hibbeler, r. Tekutina.

Riešenie

Špecifická hmotnosť y tekutiny je produktom jej hustoty v dôsledku zrýchlenia gravitácie, preto sa rovnica relatívneho tlaku môže vyjadriť nasledovne:

PZlyhať = γ.a

Relatívny tlak na spodnej časti nádrže je spôsobený hmotnosťou glycerínového stĺpca a tlaku benzínu a je nezávislý od formy nádrže:

PZlyhať = γplyn . aAB + γGly . aBc = (45.3 x 2 + 78.7 x 3) lb/ft2 = 326.7 lb/ft2

Odkazy

  1. Cimbala, C. 2006. Mechanika tekutín, základov a aplikácií. MC. Graw Hill.
  2. Hibbeler, R. 2015. Tekutina. 1. Edimatizovať. Pearson.
  3. Mott, r.  2006. Tekutina. 4. Vydanie. Pearson Vzdelanie.
  4. Sedí, a. 2006. Tekutina mechanika, fyzický úvod. Alfa omega.
  5. Streeter, v. 1999. Tekutina. McGraw Hill.
  6. Zapata, f. Tlak a hĺbka. Získané z: Francesphysics.Blog.com.