Pravidelné vlastnosti polygónov, prvky, uhly, príklady

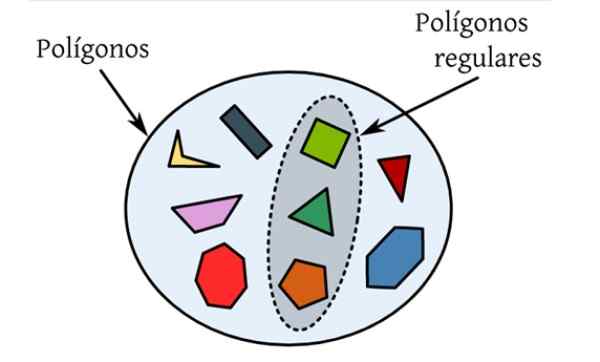
Ten pravidelné polygóny Sú to tí, ktorí majú všetky svoje strany a rovnaké vnútorné uhly. Na nasledujúcom obrázku existuje súbor rôznych polygónov, ktoré sú ploché čísla obmedzené uzavretou krivkou a iba tie, ktoré sú zvýraznené, spĺňajú podmienky, ktoré majú byť pravidelné.

Napríklad rovnostranný trojuholník je pravidelný polygón, pretože jeho tri strany merajú rovnako, ako aj vnútorné uhly, ktoré majú hodnotu 60 °.

postava 1. Pravidelné polygóny sú tie, ktorých strany a vnútorné uhly sú rovnaké, napríklad rovnostranný trojuholník a štvorec. Zdroj: Wikimedia Commons.

Štvorec je štvoruholník so štyrmi stranami rovnakej miery a ktorých vnútorné uhly sú 90 °. Nasleduje pravidelný pentagón, s piatimi stranami rovnakej veľkosti a piatimi vnútornými uhlami po 108 °.

Keď je polygón pravidelný, toto slovo sa pridá k jeho osobitnému názvu, takže máme pravidelný šesťuholník, pravidelný heptagon atď.

[TOC]

Vlastnosti bežných polygónov

Najdôležitejšie vlastnosti bežných polygónov možno zhrnúť takto:

-Strany merajú rovnako, preto sú rovnostranné prostriedky.

-Byť Rovnomerný, No, všetky jeho vnútorné uhly majú rovnakú mieru.

-Vždy sa môžu zaregistrovať v obvode, čo znamená, že sa dokonale zapadajú do jedného, ​​ktorý sa volá ohraničený obvod.

-Pre pravidelný polygón N strany je miera vnútorného uhla α:

a = [180 (n-2)]/n

-N-3)/2 Diagonaly môžu byť čerpané z vrcholov polygónu, či už pravidelné alebo nie.

-Súčet exteriérové ​​uhly Rovná sa 360 °.

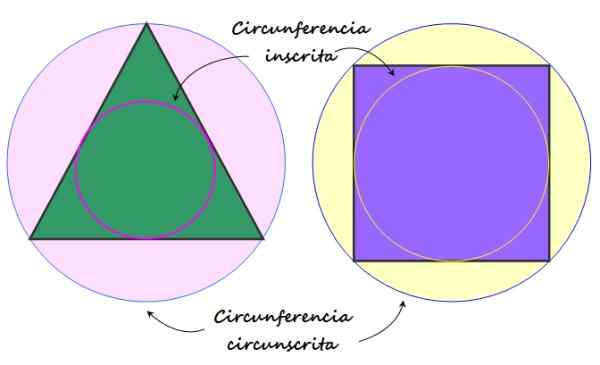Obrázok 2. Registrovaný obvod a obvod ohraničené pravidelným mnohouholníkom. Zdroj: f. Zapata.

Prvky pravidelného polygónu

Potom uvádzame hlavné prvky pravidelného polygónu, vizualizované na spodnej postave.

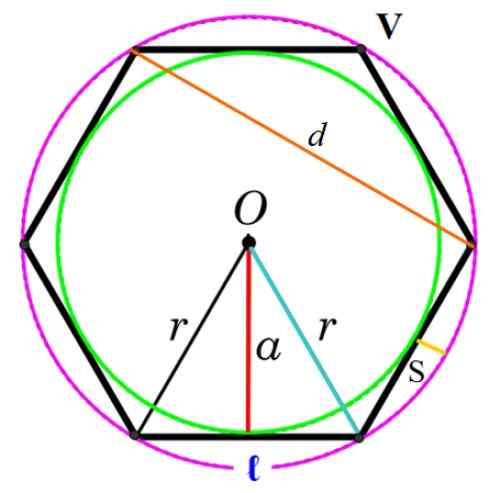Obrázok 3. Prvky pravidelného polygónu. Zdroj: f. Zapata.

Vrchol

Spoločný bod, ktorý má dve po sebe idúce strany, označené ako V na obrázku.

Strana

Je to segment, ktorý sa spája s dvoma po sebe idúcimi vrcholmi polygónu a je označený ako ℓ alebo l.

Diagonálny

Segment, ktorý sa spája s dvoma nekonečnými vrcholmi polygónu, na obrázku je označený ako d.

Stred

Je to spoločné centrum registrovaného obvodu a ohraničené obvody označené listom alebo. Dá sa tiež považovať za jediný bod, ktorý Equidista z vrcholov a stredných bodov na každej strane.

Rozhlas

Je to rádio r ohraničeného obvodu a zhoduje sa s vzdialenosťou medzi O a vrcholom.

Môže vám slúžiť: axiómy pravdepodobnosti: typy, vysvetlenie, príklady, cvičenia

Apotém

To sa nazýva apotém na polomer obvodu uvedeného v mnohouholníku, ktorý je znázornený na obrázku listom do. Apotém je kolmá na bok a spája ho stredom O (červený segment na obrázku 3).

Poznanie polomeru R a dĺžky strany sa apothém vypočíta podľa:

Pretože v skutočnosti je apothém jednou z kategórií obdĺžnika (pozri obrázok 3), druhý kateto je hodnota ℓ/2 (polovica jednej strany) a hypotenusu rádio r mnohouholníka.

Keď sa na uvedený trojuholník aplikuje veta Pythagoras, táto rovnica sa získa, čo platí nielen pre šesťuholníkov, ale aj pre akýkoľvek pravidelný polygón.

Centrálny uhol

Je to uhol, ktorého vrchol sa zhoduje so stredom alebo ktorého strany sú segmenty, ktoré spájajú stred s dvoma po sebe idúcimi vrcholmi. Jeho miera v sexuálnych stupňoch je 360 ​​°/n, kde n Je to počet strán mnohouholníka.

Mokra

Je to rozdiel medzi polomerom mnohouholníka a apotémom (pozri obrázok 3). Označovanie Sagity ako S:

S = r - a

Obvod a oblasť

Obvod

Ľahko sa vypočíta pridaním dĺžok strán. Pretože akákoľvek strana je rovnaká dĺžka l a existujú n strany, obvod P je vyjadrený ako:

P = n.L

Oblasť

V pravidelnom mnohouholníku je plocha A daná produktom medzi polostrachom (polovica obvodu) a dĺžkou apotheme do.

A = p.A /2

Keďže obvod závisí od počtu strán n, ukázalo sa, že:

A = (nl).A /2

Dva pravidelné polygóny môžu mať rovnaký obvod, aj keď nemajú rovnaký počet strán, pretože by to potom záviselo od dĺžky bokov.

V knihe V Zbierka, Matematik Alexandria (290-350), posledný z veľkých gréckych matematikov staroveku, ukázal, že medzi všetkými pravidelnými polygónmi s rovnakým obvodom je ten s najväčšou oblasťou s najväčším počtom strán strany.

Uhly

Obrázok 4 zobrazuje príslušné uhly v pravidelnom mnohouholníku označený gréckymi písmenami a, β a y.

Centrálny uhol

Predtým spomenieme centrálny uhol, medzi prvkami pravidelného polygónu, je to uhol, ktorého vrchol je v strede polygónu a strany sú segmenty, ktoré spájajú stred s dvoma po sebe idúcimi vrcholmi.

Na výpočet miery centrálneho uhla a je 360 ​​° vydelené n, počet strán. Alebo 2π radiány medzi n:

Môže vám slúžiť: Injektívna funkcia: z čoho pozostáva, na čo ide a príklady

a = 360 °/n

Rovnocenný v Radians::

a = 2π /n

Vnútorný uhol

Na obrázku 4 je vnútorný uhol β ten, ktorého vrchol sa zhoduje s jednou z obrázkov a jeho strany, sú tiež strany obrázku. Vypočíta sa v sexuálnych stupňoch:

p = [180 (n-2)]/n

Alebo v Radians pomocou:

p = [π (n-2)]/n

Vonkajšie uhly

Sú označené gréckym listom γ. Na obrázku sa pozoruje, že y + β = 180 °. Preto:

γ = 180 ° - β

Súčet všetkých vonkajších uhlov na pravidelný polygón je 360 ​​°.

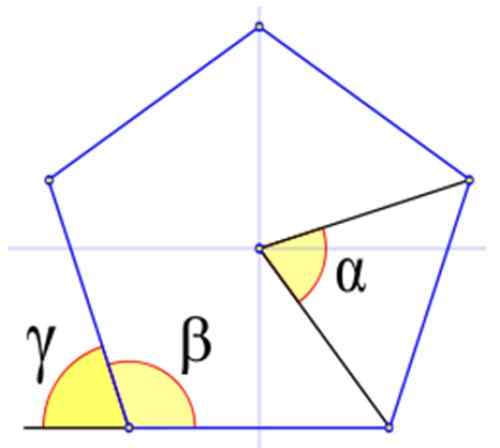Obrázok 4. Uhly v pravidelnom mnohouholníku, v tomto príklade pravidelný Pentagon. Zdroj: Wikimedia Commons.

Príklady pravidelných polygónov

Nižšie máme prvých 8 pravidelných polygónov. Poznamenávame, že so zvyšovaním počtu strán sa polygón stáva čoraz viac k obvodu, v ktorom sú registrované.

Dokážeme si predstaviť, že dĺžka dĺžky bokov je čoraz malými a zvyšuje ich počet, dostávame obvod.

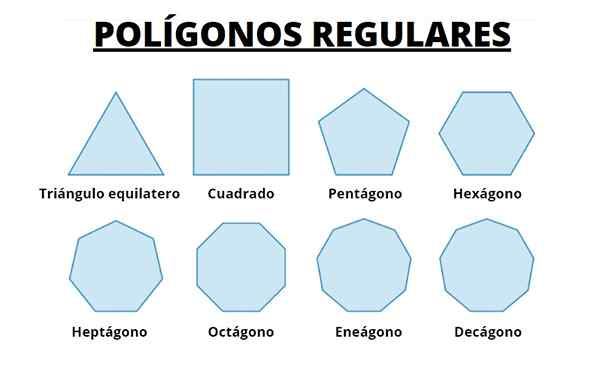Obrázok 5. Prvých osem pravidelných polygónov. Zdroj: Wikimedia Commons.

- Pravidelné polygóny v každodennom živote a prírode

Pravidelné polygóny sa nachádzajú všade v každodennom živote a dokonca aj v prírode. Pozrime sa na niekoľko príkladov:

Dopravné signály

V značení vidíme na diaľniciach a cestách oplývajú pravidelnými polygónmi, ako sú rovnostranné, štvorcové a rhombusové trojuholníky. Na obrázku 6 vidíme signálny signál s vysokým obsahom.

Obrázok 5.- Dopravný signál s osemuholníkovým tvarom. Zdroj: Pixabay.

Nábytok

Nespočetné kusy nábytku sú napríklad štvorcové, ako charakteristická geometrická postava, ako aj veľa stolov, stoličiek a brehov je štvorcový. Paralepiped je zvyčajne škatuľka s obdĺžnikovými stranami (čo nie je pravidelný polygón), ale môžu tiež vyrobiť štvorcový štvorcový.

Architektúra a výstavba

Dlaždice alebo dlaždice podlahy a steny, a to v domovoch aj v uliciach, majú často formu bežných polygónov.

Olovky sú povrchy pokryté výlučne dlaždicami, ktoré majú rozmanité geometrické postavy. S trojuholníkom môžu byť štvorcový a šesťuholníkovitý pravidelný tesselves, tie, ktoré na dokonale povlaky používajú iba jeden typ postavy, bez prázdnych priestorov (pozri obrázok 6).

Budovy tiež využívajú bežné polygóny v prvkoch, ako sú okná a dekorácia.

Obrázok 6. Štvorcová dlaždica. Zdroj: Pixabay.

- Pravidelné šesťuholníky v prírode

Prekvapivo je pravidelný šesťuholník.

Môže vám slúžiť: diskrétne rozdelenie

Plásty vyrobené včelami na skladovanie medu majú veľmi približný tvar na pravidelný šesťuholník. Ako poznamenal pappus Alexandrie, týmto spôsobom včely optimalizujú priestor na uloženie čo najviac medu.

A v škrupine korytnačiek a snehových vločiek sú tiež pravidelné šesťuholníky, ktoré tiež prijímajú rôzne veľmi krásne geometrické tvary.

Cvičenie

Pravidelný šesťuholník je súčasťou polkruhu polomeru 6 cm, ako je to znázornené na obrázku. Aká je hodnota tieňovanej oblasti?

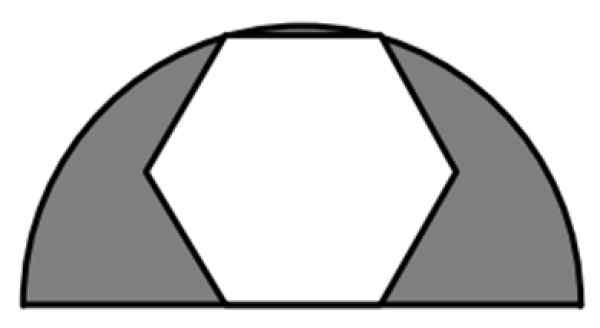Obrázok 7. Pravidelný šesťuholník registrovaný v polkruhu. Zdroj: f. Zapata.

Riešenie

Zatienená plocha je rozdiel medzi oblasťami polomerov R = 6 cm a úplnou šesťuholníkovou plochou, pravidelným 6 -vedeným polygónom. Takže budeme potrebovať vzorce pre oblasť každej z týchto čísel.

Plocha

Do₁ = π r² /2 = π (6 cm)² /2 = 18π cm²

Pravidelná šesťuholníková oblasť

Vzorec na výpočet oblasti bežného polygónu je:

A = p.A /2

Kde P Je to obvod a do Je to apothém. Pretože obvod je súčet strany, budeme potrebovať ich hodnotu. Pre pravidelné šesťuholník:

P = 6ℓ

Preto:

A = 6ℓa /2

Na nájdenie hodnoty bokov ℓ je potrebné zostaviť pomocné čísla, ktoré vysvetlíme nižšie:

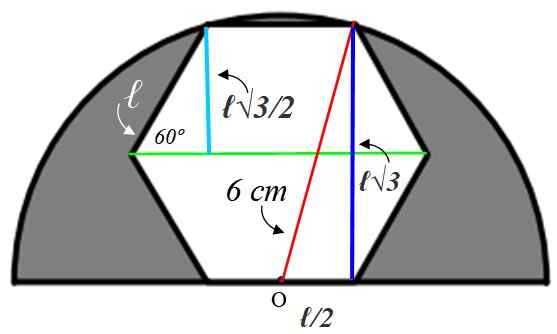
Začnime malým trojuholníkom obdĺžnika vľavo, ktorého hypotenus je ℓ. Stojí za to vnútorný uhol šesťuholníka:

a = [180 (n-2)]/n = α = [180 (6-2)]/6 = 120 °

Polomer, ktorý sme nakreslili v Bisecta Green v tomto uhle, preto je akútny uhol malého trojuholníka 60 °. S poskytnutými informáciami je tento trojuholník vyriešený a nájde svetlo modrú stranu, ktorá meria rovnako ako apothém:

Oproti cateto = a = ℓ x sin 60 ° = ℓ√3 / 2 cm

Táto hodnota je dvojnásobkom tmavomodrej nohy veľkého trojuholníka vpravo, ale z tohto trojuholníka vieme, že preprava meria 6 cm, pretože je to polomer polkruhu. Zostávajúci kateto (nižšie) má hodnotu ℓ/2, pretože bod alebo je v strede strany.

Pretože vnútorné uhly tohto trojuholníka nie sú známe, môžeme pre neho zvýšiť vetu Pythagorov:

36 = 3 ℓ² + ℓ² / 4

(13/4) ℓ² = 36 → ℓ = √ (4 x36) /13 cm = 12 /√13 cm

Pri tejto hodnote sa vypočíta apothém:

a = ℓ√3 /2 cm = (12 /√13) x (√3 /2) cm = 6√3 /√13 cm

Zavolajme a₂ do pravidelnej oblasti šesťuholníka:

= 28. 8 cm²

Plocha

Do₁ - Do₂ = 18π cm²  - 28.8 cm² = 27.7 cm²

Odkazy

1. Baldor, a. 1973. Geometria a trigonometria. Stredoamerický kultúrny úvodník.
2. Užite si matematiku. Výplach. Získané z: Vychutnajte si.com.
3. A. Do. 2003. Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
4. Šesťuholníky v prírode. Získané z: Malvargamath.Slovník.com.
5. Jiménez, r. 2010. Matematika II. Geometria a trigonometria. Druhé vydanie. Sála.
6. Pravidelné polygóny. Získané z: kamarát.inžinierstvo.Usac.Edu.Gt.
7. Wikipedia. Apotém. Obnovené z: je.Wikipedia.orgán.