Karteziánska rovina

Čo je to karteziánske lietadlo?

On Karteziánska rovina Skladá sa z páru priamok čiary kolmých na seba a ktorá sa pretína v jednom bode. Jeden z riadkov je vertikálny a druhý vodorovná, pričom sa berie do bodu križovatky ako pôvod systému.

Cieľom je ľahko lokalizovať akýkoľvek plochý bod cez pár hodnôt: koordinovať. Za týmto účelom je na každom z riadkov konštruovaná stupnica s celkovými číslami, sú kladné písané jedným smerom a negatívmi na druhom, ako je znázornené na nasledujúcom obrázku:

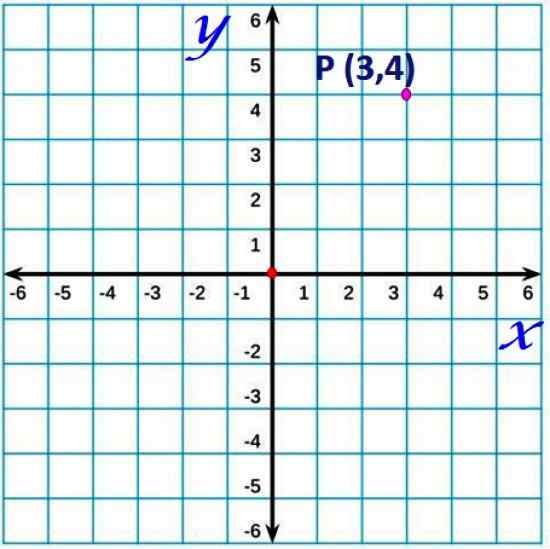
postava 1. Bod v karteziánskom lietadle. Zdroj: f. Zapata.

Konvenciou sa horizontálna os obvykle nazýva x a vertikálna os ako os a.

Akýkoľvek bod lietadla bude mať súradnice špecifikované usporiadaným párom (X, y). Napríklad bod P súradnice (3,4), ktorý sa nachádza 3 jednotky napravo od pôvodu a 4 jednotky hore, na hornom obrázku. Je to podobné ako mapa, ktorá označuje zemepisnú šírku a dĺžku určitého miesta.

Pretože sú potrebné dve súradnice, hovorí sa, že lietadlo je dve rozmerové, ale koncept sa ľahko rozšíri na tri rozmery, čím sa pridá viac súradnicovej osi, ktorá sa zvyčajne označuje ako os Z. V tomto prípade sa súradnice formujú (X a z).

Karteziánske lietadlo dostáva svoje meno od francúzskeho vedca René Descartes (1596-1650), ktorý ho vo svojej práci formalizoval Reč z roku 1637, hoci v dielach Apollonius z Perga (262-190 AC), matematikov, ktorý objavil kužeľové krivky: obvod, Ellipse, podobenstvo a hyperbola, objavil kužeľové krivky: obvod, obvod, podobenstvo a hyperbola.

Môže vám slúžiť: Rozdiel kociek: vzorce, rovnice, príklady, cvičenia

Charakteristiky karteziánskej roviny

- Ako on X os x Ako Os y Nekonečne rozširujú na oboch koncoch a pretínajú sa kolmo (v uhle 90 stupňov). Táto funkcia sa nazýva ortogonalita.

- Bod, v ktorom sa obe osi pretínajú ako pôvod alebo nulový bod.

- Koordinovaný systém rozdeľuje lietadlo do štyroch oblastí nazývaných kvadranty.

- Miesta v súradnicovej rovine sú opísané ako usporiadané páry.

- Každý bod na karteziánskej rovine je spojený s jedinečnou súradnicou X a súradnicou a jedinečným.

Prvky karteziánskeho lietadla

Prvky karteziánskej roviny sú nasledujúce:

-Ten numerické čiary ani koordinovať osi x a y, Ak je to lietadlo. Os a Prijímajte názov osi súradnicov, zatiaľ čo osi X Je to os Abscissa. Pokiaľ ide o vesmír, potom sa pridá osi z, schopný reprezentovať výšku aj hĺbku.

-On pôvod, čo je bod priesečníka osí.

-Ten kvadranty, ktoré sú regióny, ktoré súradnicové osi určujú v rovine a sú započítané v opačnom smere k hodinovým rukám, počnúc prvým kvadrantom. Sú definované takto:

• Prvý kvadrant: sekery X a a pozitívny.
• Druhý kvadrant: zodpovedajúci zápornej osi x a a pozitívnej osi.
• Tretí kvadrant: Má obe záporné osi.
• Štvrtý kvadrant: s kladnou osou x a a negatívnou osou.

Všeobecne platí, že kvadranty sú označené v rímskych číslach, ako je toto:

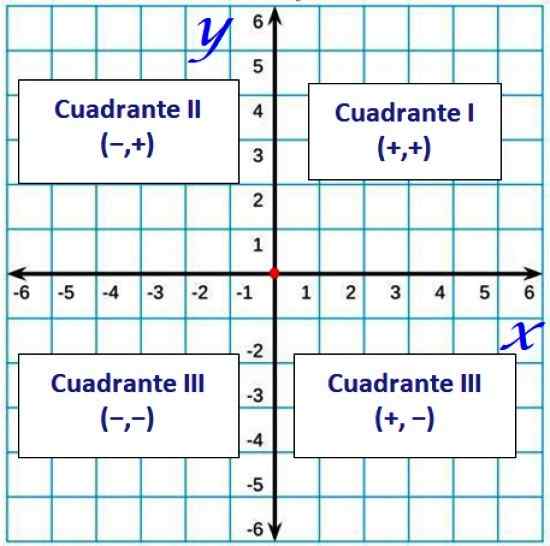Obrázok 2. Cuadrants v karteziánskom lietadle. Zdroj: f. Zapata.

Objednané páry a vzdialenosť medzi dvoma bodmi

Usporiadané páry sú súradnice každého bodu, v ktorých je súradnica X vždy umiestnená na prvom mieste, ako v príklade na obrázku 1. Súradnice (3,4) bodu P naznačujú, že to naznačujú x = 3 a y = 4.

Na tomto ďalšom obrázku nižšie je bod P patrí do kvadrantu IV a má súradnice (2; −1.5). Všimnite si, že premietaním riadkov z súradnicových osí do bodu P tvorí obdĺžnik. To je dôvod, prečo sa nazývajú aj karteziánske súradnice obdĺžnikové súradnice.

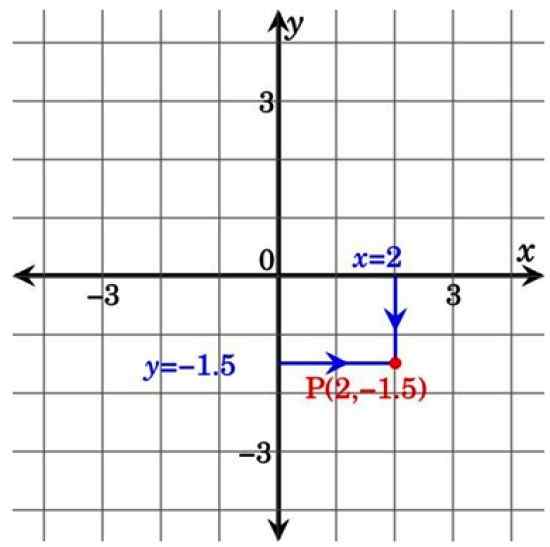Obrázok 3. Bod na karteziánskej rovine. Zdroj: Wikimedia Commons.

Aplikácie karteziánskeho lietadla

Karteziánske lietadlo má veľa aplikácií v mnohých oblastiach. Descartes ho spočiatku predstavil do grafových kriviek kriviek v lietadle, a preto sa považuje za otca analytickej geometrie.

Môže vám slúžiť: Cruz Product

Jeho použitie sa však rozširuje na grafy všetkých druhov vzťahov a funkcií, napríklad:

-Postupujte podľa trajektórie tela s parabolickým, kruhovým alebo zakriveným pohybom všeobecne.

-Graficky určte spôsob, akým sú dve premenné spojené funkciou.

-Vyhľadajte body na plochej pôde, aby ste uľahčili merania na nich.

Odkazy

1. Matematika je zábava. Karteziánske súradnice. Získané z: Mathsisfun.com/dáta/karteziánske koordináty.
2. Karteziánske lietadlo. Zdroj: DL.Uncw.Edu.