Prvky PentadeCágono, klasifikácia, charakteristiky, cvičenie

A Priechodantagón Je to plochá postava postavená z pätnástich priamych segmentov a uzavretá. Tento druh čísel sa volá polygón a sú pomenované podľa množstva strán, ktoré majú.

Trojuholník s tromi stranami a štvoruholníkmi zo štyroch je príkladmi veľmi známych polygónov, ale polygóny môžu mať viac strán.

postava 1.  Pravidelný pentagón s červenými vrcholmi. Zdroj: Wikimedia Commons.

Základné prvky Pentadecágono sú rovnaké ako akýkoľvek polygón, bez ohľadu na množstvo strán, ktoré má. Tieto prvky sú:

-Strany, ktoré sú segmenty, ktoré tvoria Pentadecágono celkom 15.

-Vrcholy, tiež 15, ktoré sú koncami susedných strán.

-Vnútorné uhly, Tie, ktoré sú tvorené v Pentadecágono medzi dvoma susednými stranami.

-Vonkajšie uhly, vytvorené medzi jednou stranou a predĺžením jednej z po sebe idúcich strán.

-Diagonála, Segmenty linky, ktoré sa spájajú s dvom net -adjacentným vrcholom.

[TOC]

Klasifikácia

Pentadecágono môže byť pravidelný ani nepravidelný, v závislosti od veľkosti ich strán a miery jeho vnútorných uhlov. Ak máte všetky strany a rovnaké vnútorné uhly - Quilátero a Estgest - je to pravidelné, ako je znázornené na obrázku 1, inak je nepravidelný.

Dá sa tiež klasifikovať ako vypuklý ani konkávny. Konkávny pentagón má jeden alebo viac vnútorných uhlov väčších ako 180 °, zatiaľ čo jeden vždy konvex má vnútorné uhly menšie ako 180 °. Pravidelný pentagón je konvexný.

Ďalšie klasifikačné kritériá sa berú do úvahy, ak sú jeho nekontrolované strany - alebo ich rozšírenia - rezané alebo nie. Keď nie sú rezané, ako v prípade obrázku 1, hovorí sa, že ide o jednoduchý pentadecágon. A ak sú rezané, potom je to zložité.

Môže vám slúžiť: analytická geometria

Pravidelný Pentagon

Pravidelný Pentagon, ktorého strany a vnútorné uhly majú rovnaké opatrenie, je postava veľkej symetrie, pretože pre tie, ktoré boli predtým opísané, sú definované nasledujúce ďalšie prvky:

-Stred: Bod, ktorý sa rovnajú vrcholom a bokom.

-Rozhlas: Vzdialenosť od stredu k jednému z pravidelných vrcholov Pentagonu.

-Centrálny uhol: Ten, kto má svoj vrchol v strede postavy a jeho strany, prechádza dvoma susednými vrcholmi.

-Apotém, Je to kolmý segment, ktorý sa spája s stredom jednej strany so stredom obrázku.

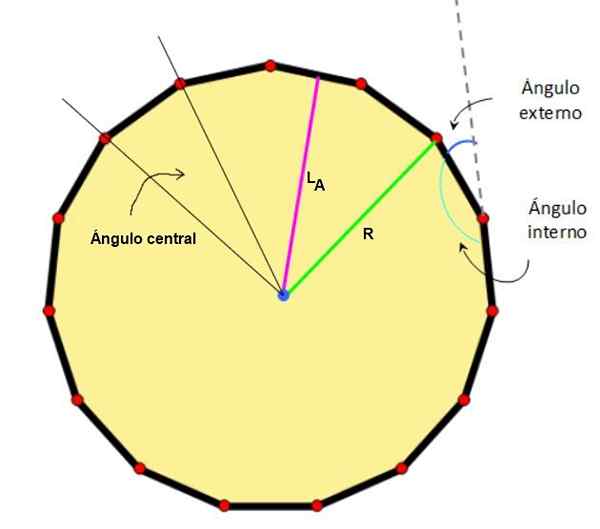Obrázok 2. Centrum, apothém, rádio a pozoruhodné uhly pentadecágono. Zdroj: Wikimedia Commons/F. Zapata.

- Charakteristiky pravidelného Pentagonu

Vnútorné uhly

Nasledujúci vzorec sa používa na výpočet miery I vnútorných uhlov akéhokoľvek pravidelného polygónu, kde n Je to počet strán:

V tomto vzorec, opatrenie I prichádza v stupňoch, na jeho exprimovanie v Radianoch, sa vynásobí faktorom π/180. Pozrime sa, čo je miera vnútorných uhlov bežného Pentagonu, nahradenie n = 15:

I = [(15-2) × 180 °]/15 = 156 °

Rovnocenné s Radians 13π/15. Pretože vnútorné uhly pravidelného Pentagónu sú menšie ako 180 °, je to konvexný mnohouholník.

Súčet vnútorných uhlov

Je možné vypočítať súčet vnútorných uhlov pomocou nasledujúceho vzorca:

S = (n-2) x 180 °

Ako vždy, n predstavuje počet strán. Tento vzorec je platný pre n = 3, 4, 5 .. .

Robiť n = 15 dostaneme:

S = (15 - 2) x 180 ° = 2340 °

Vonkajšie uhly

Vnútorný uhol a vonkajší uhol sú doplnkové, to znamená, že jeho súčet je 180 °, ako je uvedené na obrázku 2. Preto vonkajší uhol opatrení Pentadecágono:

Môže vám slúžiť: konjugovaný binomický: ako je vyriešený, príklady, cvičenia

180 ° - 156 ° = 24 °.

Obvod a oblasť

Obvod je miera obrysu polygónu a ľahko pridáva všetky strany. Jo do Je to dĺžka strany, stačí sa vynásobiť n, Počet strán.

Pre pravidelný Pentagon strany A je obvod P:

P = 15a

Ak je to nepravidelný obrázok, v ktorom sa líši miera strán, obvod dodáva dĺžku všetkých jeho strán.

Pokiaľ ide o oblasť, môžeme ju vypočítať niekoľkými spôsobmi. Napríklad máme vzorec, ktorý vám umožní získať ho poznať dĺžku A jej strany:

Vykonanie uvedených operácií zostáva približne:

A = 17 6426 ÁNO²

Existuje iná možnosť, ktorá sa vzťahuje na bežné polygóny. Ide o ich rozdelenie na základné trojuholníky rovnajúce sa mnohouholníkom. Výška trojuholníka je dĺžka apotémie l_Do, definované vyššie.

Plocha uvedeného trojuholníka sa vypočíta s dobre známym vzorcom: Base X výška /2. Týmto spôsobom je oblasť jediného trojuholníka:

Oblasť = a. L_Do /2

Ak chcete mať celkovú plochu polygónu, stačí sa vynásobiť počtom strán n, čo je v tomto prípade 15:

A = 15 štúp l_Do /2

A pretože obvod obrázku je p = 15 šu, potom:

A = plek_Do /2

Diagonála

Diagonály sú segmenty, ktoré zjednocujú dva nekontrolované vrcholy, ako je uvedené vyššie. Vedieť, koľko diagonálov má pravidelný polygón n Strany, vrátane Pentadecágono, je tu nasledujúci vzorec:

Kde d je počet diagonálov.

Teraz nahradíme n = 15, aby sme získali celkové diagonály:

Môže vám slúžiť: Pravidelné polygóny: vlastnosti, prvky, uhly, príklady

D = [15 × (15-3)]/2 = 90 diagonálov.

Konštrukcia s pravidlom a kompasom

Pentadecágono je postavený s pravidlom a kompasom začínajúcim od obvodu. 360 ° sa musí rozdeliť na 15 rovnakých častí po 24 °. Najprv sa vykonávajú pomocné konštrukcie uvedené v animácii, aby sa získal uhol 60 °, ktorý sa rozdelí na 36 ° a 24 °.

Obrázok 3. Konštrukcia s pravidlom a kompasom pravidelného Pentagonu. Zdroj: Wikimedia Commons.

Cvičenie

Ak obvod Pentadecágono zaregistrovaný v kruhu polomeru R je 12,56 cm. Vypočítať:

a) rádio.

b) Vaša oblasť.

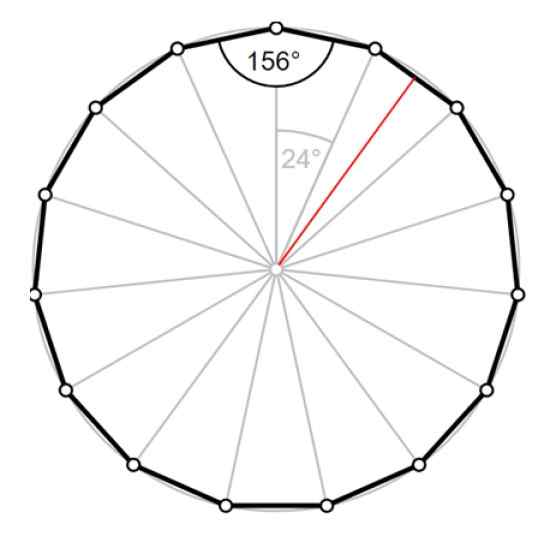Obrázok 4. PentadeCágono: Centrálny uhol, vnútorný uhol a červený apothémia. Zdroj: Wikimedia Commons/F. Zapata.

Roztok

Obvod je p = 15 šcer = 12.56 cm preto strana z Pentadecágono je 0.8373 cm. Rádio Môžeme ho vypočítať pomocou jedného z trojuholníkov na obrázku 4.

Apothem l_Do zodpovedá výške trojuholníka, nakresleného červenou farbou, ktorá rozdeľuje uhol 24 ° do dvoch uhlov po 12 ° každý.

Existujú dva pravé trojuholníky s vnútorným uhlom po 12 ° a pre niektorého z nich môžeme použiť trigonometriu na nájdenie hypotenusu, čo je dĺžka R polomeru.

Tadiaľto:

sen 12 ° = (a /2) /r

R = (a /2) /sen 12 ° = (0.8373 cm / 2) / sen12 ° = 2.01 cm.

Riešenie B

Pomocou vzorca môžeme vypočítať oblasť Pentadecágono:

A = plek_Do /2

Už poznáme obvod P = 12.56 cm a dĺžka apothémie sa vypočíta do tangentom alebo 12 ° kozínu:

Cos 12 ° = l_Do / R

L_Do = R. cos 12 ° = 2.01 cm. cos 12 ° = 1.97 cm

Výmena:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Učiť sa matematiku. Geometrické postavy. Získané z: Rodrigoanchorena.Wixsite.com.
3. Matematika. Prvky polygónu a jeho klasifikácie. Získané z: Sangakoo.com.
4. Wikipedia. Pentadecágono. Obnovené z: je.Wikipedia.orgán.
5. Wolfram matematický svet. Pentadecagon. Obnovené z: Mathworld.Valfram.com.