Kvantové čísla pre to, čo sa používa a čo sú

Ten nKvantové umejky Používajú sa na opis kvantového stavu elektrónov v atóme a vznikajú v roztoku Schrödingerovej rovnice pre najjednoduchšie zo všetkých: vodík.

Schrödingerova rovnica je diferenciálna rovnica, ktorej riešenia sú Vlnové funkcie a sú označené gréckym písmenom ψ. Je možné zvýšiť nekonečné roztoky a jeho štvorec je rovnocenný s pravdepodobnosťou nájdenia elektrónu v malej oblasti vesmíru, nazývanej orbitálny.

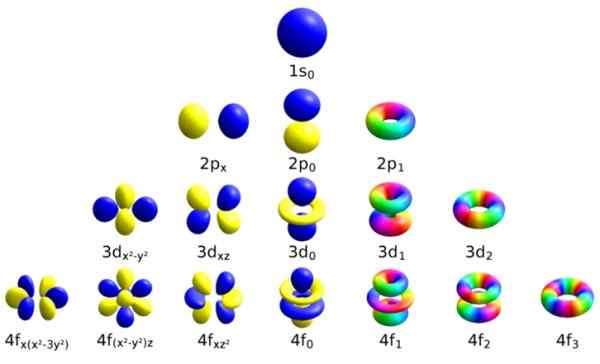
Každá z týchto atómových orbitálov sa vyznačuje určitou sadou kvantových čísel. Zdroj: Wikimedia Commons.

Každá orbitál má definované vlastnosti, ktoré ju odlišujú od ostatných, ako je napríklad energia, uhlová hybnosť a rotácia, úplne kvantová vlastnosť elektrónu a ktorá je okrem iného zodpovedná za magnetické účinky.

Spôsob, ako identifikovať každý orbitál, je rozlíšiť ho prostredníctvom súboru čísel, ktoré ho opisujú, a to sú presne kvantové čísla:

-N: Je hlavné kvantové číslo.

-ℓ: Azimutálne kvantové číslo.

-m_ℓ, Je to magnetické číslo.

-m_siež, Točiace číslo.

[TOC]

Čo sú kvantové čísla pre?

Kvantové čísla slúžia na opis stavu elektrónov vo vnútri atómu. Tento atómový model, v ktorom sa elektrón otočí okolo jadra, je nepresný, pretože nie je v súlade s atómovou stabilitou alebo s veľkým počtom pozorovaných fyzikálnych javov.

Preto dánsky Niels Bohr (1885-1962) urobil v roku 1913 odvážny návrh: elektrón sa dá nájsť iba na určitých stabilných dráhach, ktorých veľkosť závisí od celého čísla nazývaného n.

Neskôr, v roku 1925, rakúsky fyzikálny Erwin Schrödinger (1887-1961) zvýšil diferenciálnu rovnicu v čiastočných derivátoch, ktorých roztoky opisujú atóm vodíka. Sú vlnové funkcie ψ uvedené na začiatku.

Táto diferenciálna rovnica zahŕňa tri priestorové súradnice plus čas, ale keď nie je zahrnutá, riešenie Schrödingerovej rovnice je analogické s roztokom stacionárnej vlny (vlna, ktorá sa šíri medzi určitými limitmi).

Vlnové funkcie

Nezávislá časová rovnica Schrödingera je vyriešená v sférických súradniciach a riešenie je napísané ako produkt troch funkcií, jedna pre každú priestorovú premennú. V tomto súradnicovom systéme namiesto použitia súradníc karteziánskych osí X, a a z Používajú sa súradnice r, θ a φ. Tadiaľto:

Môže vám slúžiť: paralelný obvod

ψ (r, θ, φ) = r (r) ⋅f (9) ⋅g (φ)

Vlnová funkcia je nehmotná, napriek kvantovej mechanike, hovorí nám, že štvorcová amplitúda:

| ψ (r, θ, φ) |²

To znamená, že modul alebo absolútna hodnota funkcie vlny, na druhú, je skutočné číslo, ktoré predstavuje pravdepodobnosť nájdenia elektrónu v určitej oblasti okolo bodu, ktorého súradnice sú r, θ a φ.

A táto skutočnosť je niečo konkrétnejšie a hmatateľnejšie.

Ak chcete nájsť funkciu vlny, musíte vyriešiť tri bežné diferenciálne rovnice, jedna pre každú premennú r, θ a φ.

Riešenia každej rovnice, ktoré budú funkcie R (r), f (9) a g (φ), obsahujú prvé tri uvedené kvantové čísla.

Aké sú kvantové čísla?

Nižšie krátko popíšeme povahu každého kvantového čísla. Prvé tri, ako je uvedené vyššie, vznikajú z riešení Schrödingerovej rovnice.

Štvrté číslo pridal Paul Dirac (1902 - 1984) v roku 1928.

Hlavné kvantové číslo

Je označený n a označuje veľkosť povoleného orbitálu, ako aj energiu elektrónu. Čím vyššia je jej hodnota, tým viac je elektrón jadra a jeho energia bude tiež, ale na oplátku znižuje svoju stabilitu.

Toto číslo vyplýva z funkcie R (R), ktorá je pravdepodobnosťou nájsť elektrón v určitej vzdialenosti r jadra, ktoré je určené:

 Kde sa zúčastňujú nasledujúce konštanty:

-Planck Constant: H = 6 626 × 10 ^{-3. 4} J.siež
-Elektrónová hmota m_a = 9.1 × 10^-31 kg
-Elektrónové zaťaženie: E = 1.6 × 10^-19 C.
-Elektrostatická konštanta: K = 9 × 10 ⁹ N.m²/C²

Keď n = 1 zodpovedá polomeru Bohra, ktorý má hodnotu približne 5.3 × 10⁻¹¹ m.

S výnimkou prvej vrstvy sú ostatné rozdelené na čiastky alebo čiastkové úrovne. Každá vrstva má energiu vo voltovom elektróne danom:

Môže vám slúžiť: Mechanické vlny: Charakteristiky, vlastnosti, vzorce, typy

Termín Ev „Elektrónový volt“ znamená, že jednotka energie sa často používa v oblasti kvantovej fyziky. Kde n = 1, 2, 3, 4 .. . a každá hodnota n zodpovedá a vrstviť, To je označené kapitálovými písmenami:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Alebo (n = 5)
• P (n = 6)
• Q (n = 7).

Teoreticky neexistuje horná hranica pre n, ale v praxi sa pozoruje, že dosahuje iba n = 8. Najmenej možná energia zodpovedá n = 1 a je energia Základný štát.

Azimutálne kvantové číslo alebo uhlová hybnosť

Toto číslo označené kurzíva.

Môžete si napríklad užívať celé a pozitívne hodnoty medzi 0 a n-1, napríklad:

-Keď n = 1, potom ℓ = 0 a existuje jeden sub -livel.

-Ak n = 2, potom ℓ môže mať hodnotu 0 alebo 1, takže máte dve podskupiny.

-A ak n = 3, potom ℓ predpokladá hodnoty 0, 1 a 2 a sú tu 3 čiastky.

Môže sa dodržiavať neurčito, aj keď, ako už bolo uvedené, v praxi n dosahuje až 8. Podsluhy sú označené písmenami: siež, p, d, F a g A zvyšujú energiu.

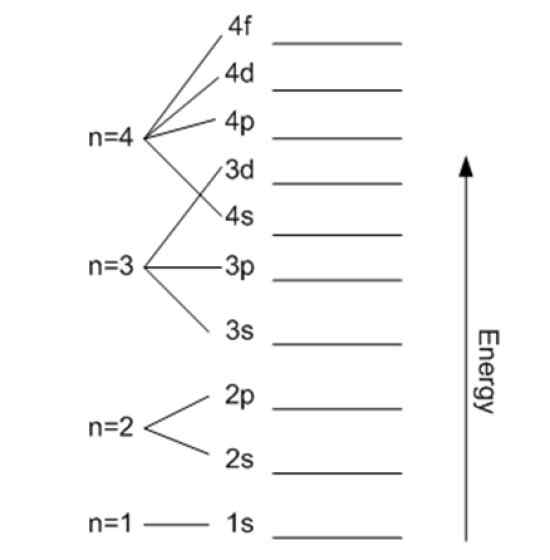Energia súvisí s hlavným kvantovým číslom. Zdroj: Wikimedia Commons.

Magnetické kvantové číslo m_ℓ

Toto číslo rozhoduje o orientácii orbitálu vo vesmíre a jeho hodnota závisí od ℓ.

Pre dané ℓ existujú (2ℓ+1) celé hodnoty m _ℓ, zodpovedajúci príslušným orbitálom. Toto sú:

-ℓ, ( - ℓ+1),… 0,… (+ℓ -1),+ℓ.

Príklad

Ak n = 2, vieme, že ℓ = 0 a ℓ = 1, potom m _ℓ Vezmite nasledujúce hodnoty:

-Pre ℓ = 0: m _ℓ = 0.
-Pre ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbitálna n = 2 má dve čiastkové úrovne, prvé s n = 2, ℓ = 0 a m _ℓ = 0. Potom máme druhý podslupku: n = 2, ℓ = 1, s 3 orbitálmi:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

Tri orbitály majú rovnakú energiu, ale inú priestorovú orientáciu.

Kvantový počet rotácie m_siež

Pri riešení Schrödingerovej rovnice v troch dimenziách sa už objavia čísla. Avšak v vodíku sa pozoruje ešte ďalšia štruktúra, ako tieto čísla nestačia na vysvetlenie.

Môže vám slúžiť: Gase Constant: Čo je, výpočet a príklady

Preto v roku 1921 ďalšia postava Wolfgang Pauli navrhla existenciu štvrtého čísla: Spinové číslo M_siež, To berie hodnoty +½ alebo -½.

S týmto číslom je opísaná veľmi dôležitá vlastnosť elektrónu, čo je točiť sa, Slovo, ktoré pochádza z angličtiny točiť sa (Otočte sa). A točenie zase súvisí s magnetickými vlastnosťami atómu.

Jedným zo spôsobov, ako porozumieť rotácii, je predstaviť si, že elektrón sa správa ako malý magnetický dipól (magnet so severnými a južnými pólmi), a to vďaka rotácii okolo svojej vlastnej osi. Odbočka môže byť v rovnakom smere ako ihly hodín alebo v opačnom smere.

Aj keď Pauli navrhol existenciu tohto čísla, výsledky experimentu, ktorý vykonali Otto Stern a Walter Gerlach v roku 1922, to už očakávali.

Týmto vedcom sa podarilo rozdeliť lúč atómov striebra aplikáciou neuniformného magnetického poľa.

Hodnota m_siež Nezávisí to od n, ℓ a m _ℓ. Graficky je reprezentovaná šípkou: šípka nahor označuje rozvrh a jeden dole po antihoráne.

Princíp vylúčenia pauli

Správanie elektrónov v atóme je zhrnuté v zásade vylúčenia Pauliho, ktorý uvádza, že dva elektróny atómu nemôžu existovať v rovnakom kvantovom stave.

Preto musí mať každý elektrón inú sadu kvantových čísel n, ℓ, m _ℓ a m_siež.

Dôležitosť kvantových čísel a tento princíp spočíva v porozumení vlastností prvkov v periodickej tabuľke: Elektróny sú usporiadané vo vrstvách podľa N a potom v čiapkach podľa ℓ a zvyšku čísel.

Odkazy

1. Alonso, m. 1971. Kvantové a štatistické základy. Inter -Americký vzdelávací fond.
2. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
3. Chang, R. 2013. Chémia. 11 VA. Vydanie. MC Graw Hill Education.
4. Eisberg-Resnick. 1989. Kvantová fyzika. Limusa - Wiley.
5. Giambattista, a. 2010. Fyzika. Druhý. Edimatizovať. McGraw Hill.
6. Rex, a. 2011. Základy fyziky. Pearson.
7. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. McGraw Hill.