Číslo Eulera alebo číslo E, koľko stojí za to, vlastnosti, aplikácie

On Číslo alebo číslo euleru e Je to dobre známa matematická konštanta, ktorá sa často objavuje v mnohých vedeckých a ekonomických aplikáciách, spolu s číslom π a ďalšími dôležitými číslami v matematike.

Vedecká kalkulačka hodí nasledujúcu hodnotu pre číslo E:

postava 1. Eulerov počet sa často objavuje vo vede. Zdroj: f. Zapata.

E = 2.718281828…

Ale je známych oveľa viac desatinných desatinných desiatkov:

E = 2.71828182845904523536…

A moderné počítače povolili desatinný bilión na číslo E.

Je to číslo iracionálny, Čo znamená, že má nekonečné množstvo desatinných miest bez opakujúceho sa vzoru (sekvencia 1828 sa objaví dvakrát na začiatku a už sa neopakuje).

A tiež to znamená, že číslo E nie je možné získať ako kvocient dvoch celých čísel.

[TOC]

História

Číslo a Bol identifikovaný vedcom Jacquesom Bernoulliom v roku 1683, keď študoval problém zloženého záujmu, ale predtým sa nepriamo objavil v dielach škótskeho matematika Johna Napiera, ktorý vynašiel logaritmy na rok 1618.

Bol to však Leonhard Euler v roku 1727, ktorý mu dal meno číslo E a intenzívne študoval svoje vlastnosti. Preto je známy aj ako Eulerové číslo a tiež ako prirodzený základ pre použité neperiánske logaritmy (exponent).

Koľko stojí číslo E?

Číslo E Vale:

E = 2.71828182845904523536…

Podporné body znamenajú, že existuje nekonečné množstvo desatinných miest a v skutočnosti sú milióny z nich známe u súčasných počítačov.

Zastúpenia čísla E

Existuje niekoľko spôsobov, ako definovať e, ktoré popisujeme nižšie:

Číslo E ako limit

Jedným z rôznych spôsobov, ako je číslo E vyjadrené, je ten, ktorý vedec Bernoulli našiel vo svojej práci o zloženom záujme:

V ktorom musíte urobiť hodnotu n Veľmi veľké množstvo.

S pomocou kalkulačky je ľahké skontrolovať n Je veľmi veľký, predchádzajúci výraz má tendenciu k hodnote a uvedené vyššie.

Môže vám slúžiť: Bijjektívna funkcia: Čo je to, ako sa to robí, príklady, cvičenia

Samozrejme sa môžeme opýtať sami seba, aké veľké sa to dá urobiť n, Snažíme sa teda s okrúhlymi číslami, ako sú napríklad:

n = 1000; 10.000 alebo 100.000

V prvom prípade dostanete e = 2.7169239… . V druhom E = 2.7181459… a v treťom je oveľa blízko k hodnote a: 2.7182682. Už to môžeme objaviť s n = 1.000.000 alebo väčší, prístup bude ešte lepší.

V matematickom jazyku postup výroby n Sa blíži a viac k veľmi veľkej hodnote, nazýva sa to limit na nekonečno A je to označené takto:

Na označenie nekonečna sa používa symbol „∞“.

Číslo E ako suma

Prostredníctvom tejto operácie je tiež možné definovať číslo E:

Obrázky, ktoré sa objavujú v menovateľovi: 1, 2, 6, 24, 120 ... zodpovedajú operácii n!, kde:

n! = n. (N-1).(N-2). (N-3) ..

A podľa definície 0! = 1.

Je ľahké overiť, že čím viac doplnkov sa pridáva, tým väčšie sa číslo dosiahne a.

Urobme niekoľko testov s kalkulačkou a pridajte čoraz viac dodatkov:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Čím viac výrazov sa pridávajú k sumre, tým viac je výsledok podobný a.

Matematici navrhli kompaktný zápis pre tieto sumy, ktoré zahŕňajú mnoho výrazov pomocou symbolu súčtu σ:

Tento expresia je zložená ako „súčet n = 0 do nekonečna 1 medzi n faktoriálnym“.

Číslo E z geometrického hľadiska

Číslo E má grafické znázornenie súvisiace s oblasťou v grafe krivky:

y = 1/x

Ak sú hodnoty x medzi 1 a E, táto oblasť má hodnotu 1, ako je znázornené na nasledujúcom obrázku:

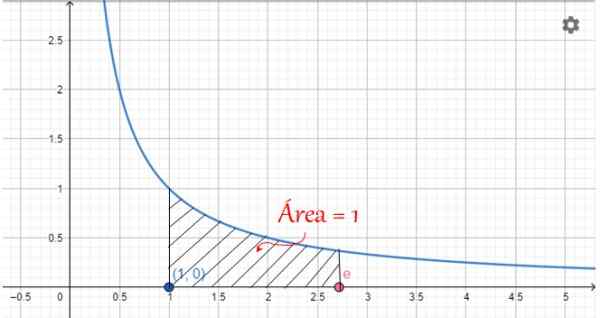Obrázok 2. Grafické znázornenie čísla E: plocha pod krivkou 1/x, medzi x = 1 a x = e hodinu. Zdroj: f. Zapata.

Číslo E Vlastnosti

Niektoré z vlastností čísla E sú:

Môže vám slúžiť: Rastúca funkcia: Ako ju identifikovať, príklady, cvičenia

-Je to iracionálne, inými slovami, nemožno ho získať jednoducho rozdelením dvoch celých čísel.

-Číslo a Je to tiež a Transcendentné číslo, čo znamená, že a Nie je to riešenie žiadnej polynómovej rovnice.

-Súvisí so štyrmi ďalšími slávnymi číslami v oblasti matematiky, konkrétne: π, i, 1 a 0, prostredníctvom identity Eulera:

a^πi + 1 = 0

-Hovory zložité čísla možno vyjadriť prostredníctvom e.

-Dnes predstavuje základ prírodných alebo neperiánskych logaritmov (pôvodná definícia Johna Napiera sa trochu líši).

-Je to jediné číslo také, že jeho neperiánsky logaritmus má hodnotu 1, to znamená:

 ln e = 1

Žiadosti

Štatistika

Číslo E sa objavuje veľmi často v oblasti pravdepodobnosti a štatistík, ktoré sa objavujú v rôznych distribúciách, ako je normálny alebo gaussovský, Poisson a ďalší.

Inžinierstvo

V inžinierstve je časté, pretože exponenciálna funkcia y = e^X Je prítomný napríklad v mechanike a elektromagnetizme. Medzi mnohými aplikáciami, ktoré môžeme citovať:

-Kábel alebo reťazec, ktorý visí s výhradou koncov, prijíma tvar krivky danej:

y = (e^X + a^-X) /2

-Kondenzátor C pôvodne vypustený, ktorý sa pripája v sérii s odporom R a zdrojom napätia V na zaťaženie, získava určité zaťaženie Q v závislosti od času t daného:

Q (t) = cv (1-e^-T/rc)

biológia

Exponenciálna funkcia y = a.a^BX, Pri konštante A a B sa používa na modelovanie buniek a rastu baktérií.

Fyzický

V jadrovej fyzike sú rádioaktívny rozklad a stanovenie AGE modelované pomocou rádiokarbonového datovania.

Hospodárnosť

Pri výpočte kompozitného záujmu vznikne číslo E prirodzene.

Predpokladajme, že máte určité množstvo peňazí P_ani, investovať do ročnej úrokovej sadzby.

Ak zostanú peniaze na 1 rok, po tomto čase budete mať:

P (1 rok) = P_ani + P_ani.i = p_ani (1+ i)

Po ďalšom roku bez toho, aby ste sa ho dotkli, budete mať:

Môže vám slúžiť: teoretická pravdepodobnosť: ako to dostať von, príklady, cvičenia

P (2 roky) = P_ani + P_ani.i + (P_ani + P_ani .i) i = P_ani +2 P_ani.i + p_ani.Jo²  = PO (1+i)²

A týmto spôsobom n Roky:

P = p_ani (1+i)ⁿ

Teraz nezabudnite na jednu z definícií E:

Vyzerá to trochu ako výraz pre p, takže musí existovať vzťah.

Distribuujeme nominálnu úrokovú sadzbu Jo v n Týmto spôsobom bude zložená úroková sadzba I/N:

P = p_ani [1+ (I/N)]ⁿ

Tento výraz vyzerá trochu viac o našom limite, ale ešte nie je presne rovnaký.

Po niektorých algebraických manipuláciách sa však dá ukázať, že vykonanie tejto zmeny premennej:

h = n/i → i = n/h

Naše peniaze P sa stáva:

P = p_ani [1+ (1/h)]^Ahoj = P_ani [1+ (1/h)]^hJo

A čo patrí medzi kľúče, aj keď je napísané listom h, Rovná sa argumentu limitu, ktorý definuje číslo E, chýba len obmedzenie limitu.

Poď robiť  h → ∞ a čo je medzi kľúčmi, sa transformuje na číslo a. To neznamená, že musíme čakať nekonečne veľký čas, aby sme si vybrali svoje peniaze.

Ak vyzeráme dobre, keď to robíme H = n/i A tendencia k ∞, čo sme skutočne urobili, je rozdeliť úrokovú sadzbu vo veľmi, veľmi malom časovom období: veľmi malé:

I = n/h

Toto sa volá Nepretržitá kapitalizácia. V tomto prípade sa množstvo peňazí ľahko vypočíta takto:

P = p_ani .a^Jo

Kde som ročná úroková sadzba. Napríklad vložením 12 až 9 % EUR ročne prostredníctvom nepretržitej kapitalizácie po jednom roku máte:

P = 12 x e^{0.09 × 1} € = 13.13 EUR

So ziskom 1.13 €.

Odkazy

1. Užite si matematiku. Zložené úroky: Periodické zloženie. Získané z: Vychutnajte si.com.
2. Figuera, J. 2000. Matematika 1. Diverzifikovaný. Edície Co-Bo.
3. Garcia, m. Číslo E v elementárnom výpočte. Obnovené z: matematiky.Cins.UCV.ísť.
4. Jiménez, r. 2008. Algebra. Sála.
5. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.