Doplnkové uhly, ktoré sú, výpočet, príklady, cvičenia

Dve alebo viac sú doplnkové uhly Ak súčet jeho opatrení zodpovedá miere plochého uhla. Miera plochého uhla, tiež nazývaného plochý uhol, v stupňoch je 180 ° a v radiánoch je π.

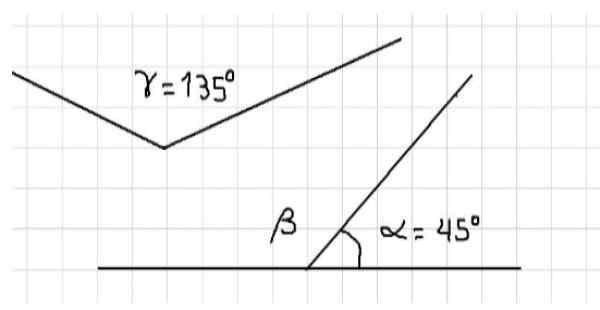
Napríklad zistíme, že tri vnútorné uhly trojuholníka sú doplnkové, pretože súčet jeho opatrení je 180 °. Tri uhly sú znázornené na obrázku 1. Z vyššie uvedeného vyplýva, že a a p sú doplnkové, pretože sú susedné a ich úplný súčet je plochý uhol.

Obrázok 1: a a p sú doplnkové. α a y sú doplnkové. Zdroj: f. Zapata.

Aj na tom istom čísle existujú uhly a a y, ktoré sú tiež doplnkové, pretože súčet ich opatrení sa rovná rozsahu plochého uhla, to znamená 180 °. Nedá sa povedať, že uhly β a γ sú doplnkové, pretože oba tupé uhly ich opatrenia sú väčšie ako 90 °, a preto ich súčet presahuje 180 ° °.

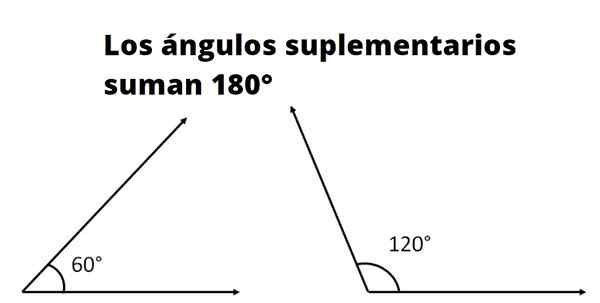Zdroj: Lafer.com

Na druhej strane je možné povedať, že miera uhla β sa rovná miere uhol y, pretože ak je p.

[TOC]

Príklady

V nasledujúcich príkladoch sa požaduje, aby našli neznáme uhly, ktoré sú uvedené s výsluchom na obrázku 2. Siahajú od najjednoduchších príkladov až po trochu komplikovanejšie, ako by mal byť čitateľ opatrnejší.

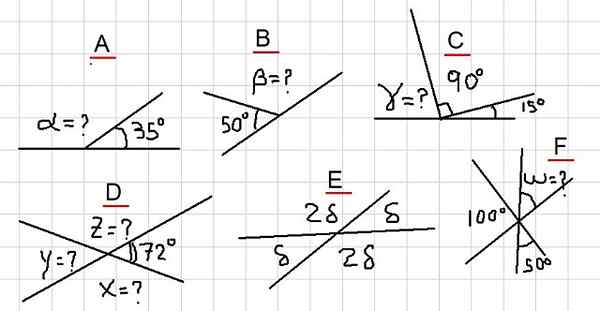Obrázok 2. Rôzne príklady doplnkových uhlov. Zdroj: f. Zapata.

Príklad a

Na obrázku máme, že susedné uhly α a 35 ° pridajú plochý uhol. To znamená a + 35 ° = 180 °, a preto je splnené, že: α = 180 °- 35 ° = 145 °.

Príklad B

Pretože p je doplnkový s uhlom 50 °, potom sa dodržiava, že β = 180 ° - 50 ° = 130 °.

Môže vám slúžiť: Aké sú prvky podobenstva? (Časti)

Príklad c

Z obrázku 2c je zaznamenaný nasledujúci súčet: γ + 90 ° + 15 ° = 180 °. To znamená, že y je doplnkový s uhlom 105 ° = 90 ° + 15 °. Predpokladá sa, že: 

γ = 180 °- 105 ° = 75 °

Príklad d

Pretože x je doplnkový s 72 °, vyplýva, že x = 180 ° - 72 ° = 108 °. Navyše a je doplnkový s x, potom y = 180 ° - 108 ° = 72 °.

A nakoniec z je doplnkový so 72 °, preto Z = 180 ° - 72 ° = 108 °.

Príklad e

Uhly A a 2A sú doplnkové, preto δ + 2A = 180 °. Čo znamená, že 3A = 180 °, a to zase umožňuje písanie: δ = 180 ° / 3 = 60 °.

Príklad f

Ak zavoláme uhol medzi 100 ° a 50 °, potom je potrebné ich doplniť, pretože sa zistilo, že ich úplný súčet je plochý uhol.

Z toho vyplýva, že u = 150 °. Ako u je proti vrcholu W, potom w = u = 150 °.

Cvičenia

Nižšie sú navrhnuté tri cvičenia, vo všetkých z nich je hodnota uhlov A a B nájdená v stupňoch, takže vzťahy znázornené na obrázku 3 sú splnené. Koncept doplnkových uhlov sa používa pri riešení všetkých z nich.

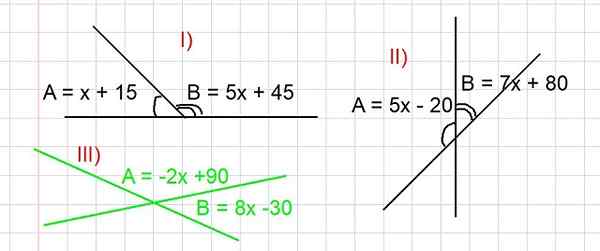Obrázok 3. Obrázok na vyriešenie cvičení I, II a III na doplnkových uhloch. Všetky uhly sú vyjadrené v stupňoch. Zdroj: f. Zapata.

- Cvičenie I

Stanovte hodnoty uhlov A a B časti I) na obrázku 3.

Riešenie

A a B sú doplnkové, kde je potrebné nahradiť a + b = 180 stupňov, potom sa výraz A a B nahradí ako funkcia x, ako sa zdá na obrázku:

(x + 15) + (5x + 45) = 180

Získava sa lineárna rovnica prvého riadku. Na jeho vyriešenie sú výrazy vyhodené: Podmienky:

6 x + 60 = 180

Môže vám slúžiť: Reálne čísla: História, príklady, vlastnosti, operácie

Rozdelenie oboch členov medzi 6 sú:

x + 10 = 30

A nakoniec vyčistenie, z toho vyplýva, že X má hodnotu 20 °.

Teraz sa musí vymeniť hodnota X, aby sa našli usporiadané uhly. Odtiaľ musíte uhli a je: a = 20 +15 = 35 °.

A z jeho časti, uhol B je b = 5*20 + 45 = 145 °.

- Cvičenie II

Nájdite hodnoty uhlov A a B časti II) na obrázku 3.

Riešenie

Ako A a B sú doplnkové uhly, A + B = 180 stupňov. Nahradenie expresie A a B ako funkcie x uvedené v časti II) na obrázku 3 je:

(-2x + 90) + (8x - 30) = 180

Opäť sa získa rovnica prvého stupňa, pre ktorú musia byť podmienky pohodlne skupiny:

6 x + 60 = 180

Rozdelenie oboch členov medzi 6 sú:

x + 10 = 30

Kde z toho vyplýva, že X má hodnotu 20 °.

To znamená, že uhol A = -2*20 + 90 = 50 °. Zatiaľ čo uhol B = 8*20-30 = 130.

- Cvičenie III

Stanovte hodnoty uhlov A a B časti III) na obrázku 3 (v zelenej).

Riešenie

Ako A a B sú doplnkové uhly, A + B = 180 stupňov. Expresia A a B sa musí nahradiť ako funkcia X uvedená na obrázku 3, ktorú máte:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Rozdelenie oboch členov o 12, aby ste vyčistili hodnotu X, máte:

x + 5 = 15

Nakoniec sa zistí, že X má hodnotu 10 stupňov.

Teraz pokračujte v výmene hľadania uhla a: a = 5*10 -20 = 30 °. A pre uhol B: B = 7*10 + 80 = 150 °

Môže vám slúžiť: Aký je sortiment štatistík? (S príkladmi)

Doplnkové uhly v dvoch paraleloch vyrezaných secantom

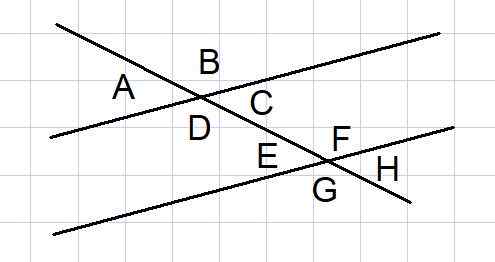Obrázok 4. Uhly medzi dvoma paralelmi rezané sekundom. Zdroj: f. Zapata.

Dve paralelné čiary rezané secantom sú obvyklá geometrická konštrukcia v niektorých problémoch. Spomedzi takýchto čiar sa tvorí 8 uhlov, ako je znázornené na obrázku 4.

Z týchto 8 uhlov sú niektoré páry uhlov doplnkové, ktoré uvádzame nižšie:

1. Vonkajšie uhly k a B a exteriéry g a h
2. Vnútorné uhly D a C a interiéry e a f
3. Vonkajšie uhly a a g a vonkajšie b a h
4. Vnútorné uhly D a E a väzni C a F

Podľa úplnosti sú rovnaké uhly tiež pomenované:

1. Vnútorné striedanie: D = f a c = e
2. Vonkajšie striedanie: a = h a b = g
3. Zodpovedajúce: a = e a c = h
4. Protiklady podľa vrcholu a = c a e = h
5. Zodpovedajúce: b = f a d = g
6. Protiklady podľa vrcholu b = d a f = g

- Cvičenie IV

V súvislosti s obrázkom 4, v ktorom uhly ukazujú medzi dvoma paralelnými čiarami rezanými sekvenciou, určte hodnotu všetkých uhlov v radiánoch, s vedomím, že uhol A = π/6 radiány.

Riešenie

A a B sú doplnkové vonkajšie uhly, preto b = π - a = π - π/6 = 5π/6

A = e = c = h = π/6

B = f = d = g = 5π/6

Odkazy

1. Baldor, J. Do. 1973.Geometria plochej a vesmíru. Stredoamerický kultúrny. 
2. Matematické zákony a vzorce. Meracie systémy. Zdroj: Ingemecanica.com.
3. Wentworth, G. Geometria planéty. Získané z: Gutenberg.orgán.
4. Wikipedia. Doplnkové uhly. Obnovené z: je.Wikipedia.com
5. Wikipedia. Dopravník. Obnovené z: je.Wikipedia.com
6. Zapata f. Goniometer: História, časti, prevádzka. Zdroj: Lifer.com