Registrovaný uhol definície kruhu, vety, príklady

On registrovaný uhol kruhu Je to ten, ktorý má svoj vrchol na obvode a jeho polo -prúžky sú suché alebo dotyčené. V dôsledku toho bude registrovaný uhol vždy vypuklý alebo plochý.

Na obrázku 1 je zastúpených niekoľko uhlov zaregistrovaných vo svojich obvodoch. Uhol ∠EDF je zaregistrovaný tým, že má svoj vrchol D na obvode a jeho dvaja semi -regrence (z) a [df) sušiaci obvod. 

postava 1. Niekoľko vpísaných uhlov na ich príslušné obvody. Zdroj: f. Zapata s geogebou.

Podobne je uhol ∠HGI zaregistrovaný, pretože má svoj vrchol v obvode a jeho suché strany na rovnaké.

Uhly ∠KJR a ∠UST sú tiež zaregistrované s obvodom. Prvá má jednu sekundovú stranu a druhú dotyčnicu, zatiaľ čo druhá má svoje dve strany dotýkajúc sa obvodu a vytvára plochý uhol roviny (180 °).

Niektorí autori nazývajú polo-inkované uhol k tomu, ktorý má jednu zo svojich strán do obvodu, ale v tomto článku sa považuje za registrovaný.

Akýkoľvek registrovaný uhol definuje alebo podvádza oblúk spojený s rovnakým. Napríklad na obrázku 2 registrovaný uhol ∠ABC podvádza oblúk dĺžky d.

Rovnaký obrázok ukazuje uhol ∠DOE, ktorý nie je zaregistrovaný v obvode, pretože nemá svoj vrchol na svojom obvode, ale v strede alebo.

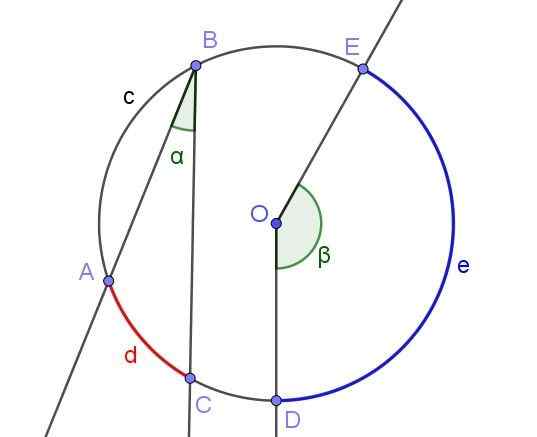Obrázok 2. Registrovaný uhol ∠ABC a centrálny uhol ∠DOE. Zdroj: f. Zapata s geogebou.

[TOC]

Centrálny uhol

Okrem registrovaného uhla, centrálny uhol, ktorý je ten, ktorého vrchol je v strede obvodu a ktorého strany sa znížili na obvod.

Môže vám slúžiť: rozdiel medzi spoločnou frakciou a desatinným číslom

Radiány Miera centrálneho uhla je kvocient medzi oblúkom, ktorý je obvodom obvodu medzi bokmi uhla a polomerom obvodu.

Ak je obvod jednotný (polomer 1), potom dĺžka oblúka v rovnakých rádiových jednotkách je miera uhla v Radianes.

A keď je miera uhla potrebná v stupňoch, potom sa v radiánoch vynásobí v radiánoch faktorom 180 °/π.

Nástroje na meranie uhlov vždy používajú centrálny uhol a dĺžku oblúka, ktoré sú priamo kalibrované v stupňoch. To znamená, že vždy, keď sa meria uhol, v pozadí sa meria dĺžka oblúka podvádzaného centrálnym uhlom.

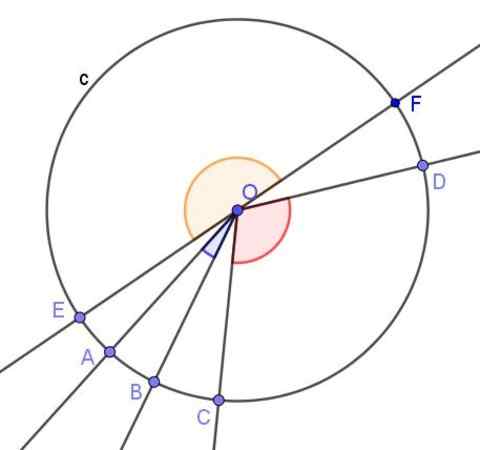Obrázok 3. Niekoľko centrálnych uhlov obvodu. Zdroj: f. Zapata s geogebou.

Vety

- Veta 1 (registrovaný uhol a centrálny uhol)

Miera registrovaného uhla je polovica miery centrálneho uhla, ak oba uhly podtuhujú rovnaký oblúk.

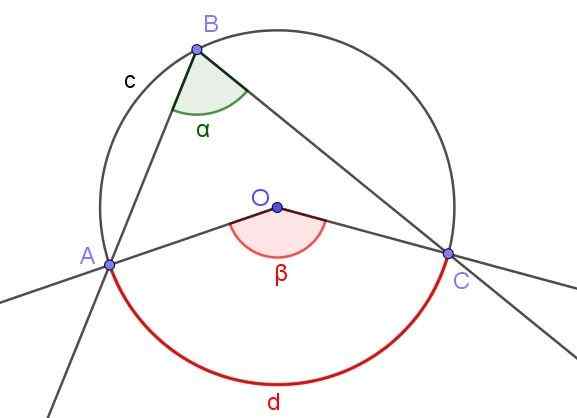Obrázok 4. Registrovaný uhol ∠ABC a centrálny uhol ∠AOC, ktorý subtituje rovnaký oblúk A⌒C. Zdroj: f. Zapata s geogebou.

Obrázok 4 zobrazuje dva uhly ∠ABC a ∠AOC, ktoré pretína rovnaký obvod Arc A⌒C.

Ak je miera registrovaného uhla a, potom je β miera centrálneho uhla dvojnásobkom miery registrovaného uhla (β = 2 a), pretože obe odpočítajú rovnaký nameraný oblúk d.

Demonštrácia 1

Na demonštráciu vety 1 sa začne niekoľko konkrétnych prípadov, až kým nedosiahne všeobecný prípad.

Môže vám slúžiť: Sandwichský zákon: Vysvetlenie a cvičenia

Predpokladajme registrovaný uhol, v ktorom jedna z jeho strán prechádza stredom obvodu, ako je znázornené na obrázku 5.

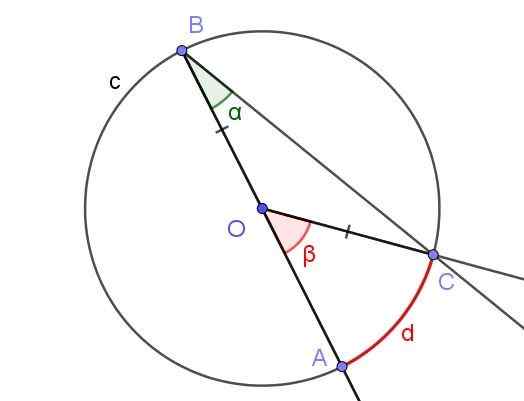Obrázok 5. Registrovaný uhol ∠ABC s bočnou stránkou [BA) cez O a centrálny uhol ∠AOC. Zdroj: f. Zapata s geogebou.

V tomto prípade sa tvorí COB Isosceles Triange, pretože [OC] = [OB].

V trojuholníku Isosceles sú uhly susediace s základňou rovnaké, preto musia ∠BCO = ∠ABC = α. Na druhej strane ∠COB = 180 ° - β.

Berúc do úvahy súčet vnútorných uhlov klasického trojuholníka, ktorý máte:

a + a + (180 ° - p) = 180 °

Kde vyplýva, že 2 a = β, alebo čo je ekvivalentné: a = β/2. To sa zhoduje s tým, čo uvádza veta 1: Miera registrovaného uhla je polovicou centrálneho uhla, ak oba uhly predkladajú rovnaké lano [AC].

Demonštrácia 1b

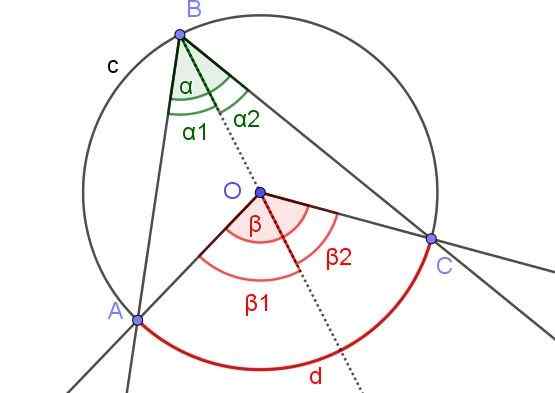Obrázok 6. Pomocná konštrukcia na preukázanie, že a = β/2. Zdroj: f. Zapata s geogebou.

V tomto prípade je vpísaný uhol ∠ABC, v ktorom je stred alebo obvod vo vnútri uhla.

Aby som demonštroval vetu 1 V tomto prípade je nakreslený polopriepustný pomocný [BO), takže existujú dva registrované uhly ∠ABO a ∠OBC susediace s uvedeným polo -rekrečným.

Podobne majú centrálne uhly β₁ a p₂ susediaci k uvedeným polopriepustným. Týmto spôsobom máte rovnakú situáciu ako v demonštrácii 1, takže je možné uviesť, že α₂ = β₂ /2 a α₁ = β₁ /2. Ako α = α₁ + α₂ a p = β₁ + p₂ Preto existuje a = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + p₂) / 2 = β / 2.

Môže vám slúžiť: typy integrálov

Na záver a = β / 2, ktorý spĺňa vetu 1.

- Veta 2

Ak dva alebo viac registrovaných uhlov podriadia rovnaký oblúk, potom majú rovnaké opatrenie.

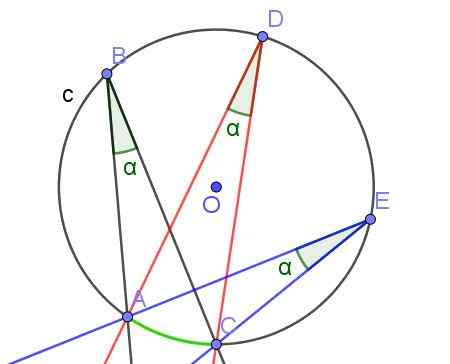Obrázok 7. Registrované uhly rovnakej miery a, pretože podriadia rovnaký oblúk A⌒C. Zdroj: f. Zapata s geogebou.

- Veta 3

Podnadpisy registrovaných uhlov Existujú rovnaké reťazce rovnakého opatrenia sú rovnaké.

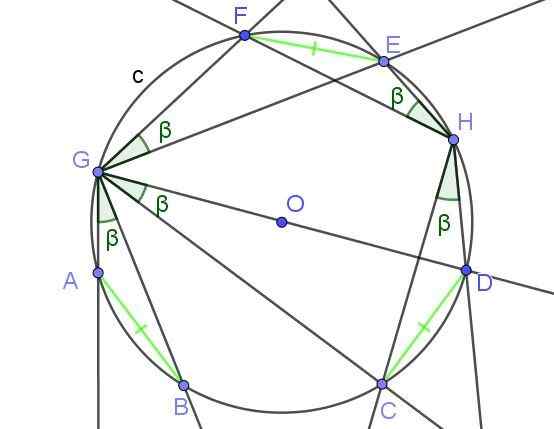Obrázok 8. Vpísané uhly, ktoré subtuse laná rovnakej miery, majú rovnakú mieru β. Zdroj: f. Zapata s geogebou.

Príklady

- Príklad 1

Demonštrujte, že vpísaný uhlový subtites Priemer je pravý uhol.

Riešenie

Centrálny uhol ∠AOB spojený s priemerom je plochý uhol, ktorého opatrenie je 180 °.

Podľa vety 1 má akýkoľvek uhol zaregistrovaný v obvode, ktorý podvádza rovnaké lano (v tomto prípade priemer), zmerajte polovicu centrálneho uhla, ktorý subtituje rovnaké lano, ktoré je pre náš príklad 180 °/2 = 90 ° ° ° °.

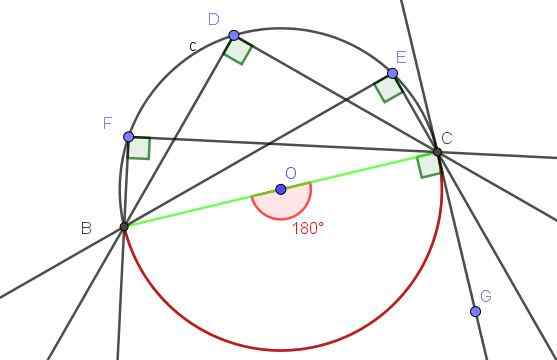Obrázok 9. Akýkoľvek registrovaný uhol, ktorý sa podmieňuje priemeru, je pravý uhol. Zdroj: f. Zapata s geogebou.

- Príklad 2

Čiara (BC) Tangent v A a A do obvodu C určuje vpísaný uhol ∠BAC (pozri obrázok 10).

Overte, či je splnená veta 1 registrovaných uhlov.

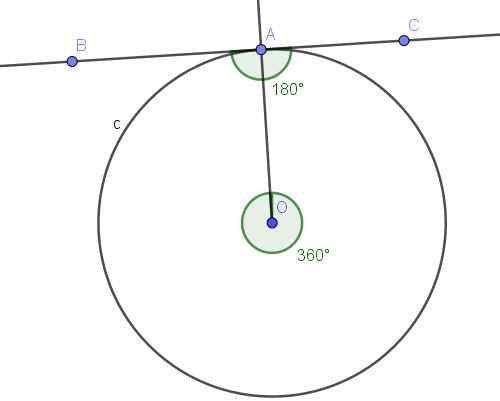Obrázok 10. Registrovaný uhlový bAC a jeho konvexný centrálny uhol AOA. Zdroj: f. Zapata s geogebou.

Riešenie

Uhol ∠BAC je zaregistrovaný, pretože jeho vrchol je na obvode a jeho strany [AB) a [AC) sú do tankujúcej do obvodu, takže je splnená definícia vloženého uhla.

Na druhej strane vpísaný uhol ∠BAC podvádza oblúk A⌒A, ktorý je úplným obvodom. Centrálny uhol, ktorý podvádza oblúk A⌒a, je konvexný uhol, ktorého miera je celý uhol (360 °).

Registrovaný uhlový subtites Meria úplný oblúk polovicu pridruženého centrálneho uhla, to znamená ∠BAC = 360 °/2 = 180 °.

So všetkými vyššie uvedenými je dokázané, že tento konkrétny prípad spĺňa vetu 1.

Odkazy

1. Plechovka. (1973). Geometria a trigonometria. Stredoamerický kultúrny úvodník.
2. A. Do. (2003). Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
3. Geometria 1. Uhly v obvode. Získané z: edu.Xunta.je/
4. Všetka veda. Navrhované cvičenia uhlov v obvode. Získané z: Francesphysics.Blog.com
5. Wikipedia. Registrovaný uhol. Obnovené z: je.Wikipedia.com