Metodika náhodného vzorkovania, výhody, nevýhody, príklady

On náhodné vzorkovanie Je to spôsob, ako zvoliť štatisticky reprezentatívnu vzorku z danej populácie. Časť zásady, že každý prvok vzorky musí mať rovnakú pravdepodobnosť, že bude vybraný.

Tombola je príklad náhodného odberu vzoriek, v ktorom je každému členovi populácie účastníkov pridelené číslo. Ak chcete zvoliť čísla zodpovedajúce oceneniam tomboly (vzorka), sa používa určitá náhodná technika, napríklad extrakt z poštovej schránky čísla, ktoré boli hodnotené na identických kartách.

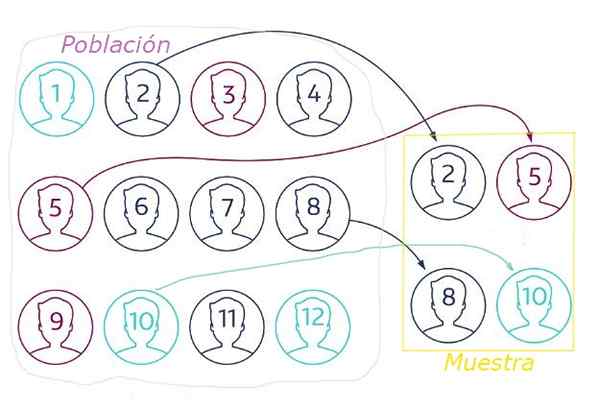postava 1. Pri náhodnom vzorkovaní sa vzorka extrahuje z náhodnej populácie určitou technikou, ktorá zaisťuje, že všetky prvky majú rovnakú pravdepodobnosť zvolenia. Zdroj: NetQuest.com.

Pri náhodnom odbernom vzorke je to nevyhnutné.

[TOC]

Veľkosť vzorky

Existujú vzorce na určenie správnej veľkosti vzorky. Najdôležitejším faktorom, ktorý je potrebné zvážiť, je, či je známa veľkosť populácie. Pozrime sa na vzorce, aby sme určili veľkosť vzorky:

Prípad 1: Veľkosť populácie nie je známa

Ak veľkosť populácie nie je známa, je možné vybrať primeranú vzorku N, aby ste určili, či je určitá hypotéza pravdivá alebo nepravdivá.

Na tento účel sa používa nasledujúci vzorec:

n = (z² P q)/(e²)

Kde:

-P je pravdepodobnosťou, že hypotéza je pravdivá.

-Q je pravdepodobnosť, že to tak nie je, preto q = 1 - p.

-E je relatívna chyba, napríklad 5% chyba má maržu E = 0,05. 

-Z súvisí s úrovňou dôvery, ktorú vyžaduje štúdia.

Môže vám slúžiť: Normálne rozdelenie: vzorec, charakteristiky, príklad, cvičenie

V normálnom distribúcii je typom (alebo normalizovanej) úroveň spoľahlivosti 90% z = 1 645, pretože pravdepodobnosť, že výsledok je medzi -1 645σ a +1 645σ, je 90%, kde σ je štandardná odchýlka.

Úroveň dôvery a ich zodpovedajúce hodnoty Z 

1.- 50% úroveň spoľahlivosti zodpovedá Z = 0,675.

2.- 68.3% úroveň spoľahlivosti zodpovedá Z = 1.

3.- 90% úroveň spoľahlivosti zodpovedajúcej z = 1 645.

4.- 95% úroveň spoľahlivosti zodpovedá Z = 1,96

5.- 95,5% úroveň spoľahlivosti zodpovedá Z = 2.

6.- 99,7% úroveň spoľahlivosti je rovnocenná s Z = 3.

Príkladom, v ktorom je možné tento vzorec aplikovať.

Je zrejmé, že nie je možné študovať a zvážiť všetky kamienky na pláži, takže je pohodlné.

Obrázok 2. Na štúdium charakteristík kamienkov na pláži je potrebné zvoliť náhodnú vzorku s reprezentatívnym počtom z nich. (Zdroj: Pixabay)

Prípad 2: Je známa veľkosť populácie

Ak je známy počet N prvkov, ktoré tvoria určitú populáciu (alebo vesmír), ak si chcete vybrať jednoduchým náhodným vzorkovaním štatisticky významnej vzorky vzorky, je to vzorec: 

n = (z²p q n)/(n e² + Z²P q)

Kde:

-Z je koeficient spojený s úrovňou dôvery.

-P je pravdepodobnosť úspechu hypotézy.

-Q je pravdepodobnosť zlyhania v hypotéze, p + q = 1.

-N je veľkosť celkovej populácie.

-E je relatívna chyba výsledku štúdie.

Príklady

Metodika na extrahovanie vzoriek veľa závisí od typu štúdie, ktorú je potrebné urobiť. Preto má náhodný odber vzoriek nespočetné množstvo aplikácií:

Môže vám slúžiť: Známky zoskupenia

Prieskumy a dotazníky

Napríklad v telefonických prieskumoch sú ľudia vybraní, aby sa s ním konzultovalo generátor s náhodnými číslami, ktoré sa vzťahujú na študovaný región.

Ak chcete uplatniť dotazník na zamestnancov veľkej spoločnosti, potom sa výber respondentov môže použiť prostredníctvom ich čísla zamestnancov alebo číslo identity karty.

Toto číslo musí byť tiež zvolené náhodne, napríklad použitím generátora náhodných čísel.

Obrázok 3. Dotazník je možné uplatniť náhodne výberom účastníkov. Zdroj: Pixabay.

Qa

V prípade, že štúdia je na častiach vyrobených strojom, musia sa časti vyberať náhodne, ale z pozemkov vyrobených v rôznych časoch dňa alebo v rôznych dňoch alebo týždňoch.

Výhody

Jednoduchý náhodný odber vzoriek:

- Umožňuje znížiť náklady na štatistickú štúdiu, pretože nie je potrebné študovať celkovú populáciu, aby sa získalo štatisticky spoľahlivé výsledky, s požadovanou úrovňou dôvery a úrovne chýb v štúdii.

- Vyhnite sa zaujatosti: Keďže výber prvkov, ktoré sa majú študovať.

Nevýhody

- Táto metóda nie je dostatočná v prípadoch, keď chcete poznať preferencie v rôznych skupinách alebo populačných vrstvách.

V tomto prípade je vhodnejšie, aby ste predtým určili skupiny alebo segmenty, na ktorých sa štúdia vykonáva. Po definovaní vrstiev alebo skupín, ak je pre každého z nich vhodné uplatniť náhodný odber vzoriek.

- Je veľmi nepravdepodobné, že sa získajú informácie o menšinových sektoroch, z ktorých niekedy je potrebné poznať ich vlastnosti.

Môže vám slúžiť: Simpson Pravidlo: vzorec, demonštrácia, príklady, cvičenia

Napríklad, ak je to kampaň drahého produktu, je potrebné poznať preferencie najbohatších sektorov menšín.

Cvičenie

Chceme študovať preferencie populácie tak, ako Cola z Coly, ale v tejto populácii neexistuje žiadna predchádzajúca štúdia, ktorej jej veľkosť nie je známa.

Na druhej strane, vzorka musí byť reprezentatívna s minimálnou úrovňou spoľahlivosti 90% a závery musia mať percentuálnu chybu 2%.

-Ako určiť veľkosť S vzorky?

-Aká by bola veľkosť vzorky, ak by sa chyba vytvorila až 5%?

Riešenie

Pretože veľkosť populácie nie je známa, na stanovenie veľkosti vzorky sa používa vzorec uvedený vyššie:

n = (z²P q)/(e²)

Predpokladáme, že existuje rovnaká pravdepodobnosť preferencie (P) našim občerstvením, ktorá nie je v poriadku (q), potom p = q = 0,5.

Na druhej strane, pretože výsledok štúdie musí mať percentuálnu chybu menej ako 2%, relatívna chyba bude 0,02.

Nakoniec hodnota Z = 1 645 produkuje úroveň spoľahlivosti 90%.

Stručne povedané, máte nasledujúce hodnoty:

Z = 1 645

P = 0,5

Q = 0,5

E = 0,02

S týmito údajmi sa vypočíta minimálna veľkosť vzorky:

N = (1 645² 0,5 0,5)/(0,02²) = 1691.3

To znamená, že štúdia s požadovanou mierou chýb a s zvolenou úrovňou dôvery musí mať vzorku respondentov najmenej 1692 jedincov, vyberených jednoduchým náhodným vzorkovaním.

Ak prejdete z chybovej marže z 2% na 5%, potom je nová veľkosť vzorky:

N = (1 645² 0,5 0,5)/(0,05²) = 271

Čo je výrazne nižší počet jednotlivcov. Záverom je, že veľkosť vzorky je veľmi citlivá na požadovanú maržu v štúdii.

Odkazy

1. Berenson, m. 1985.Štatistiky pre správu a hospodárstvo, koncepty a aplikácie. Inter -American Editorial.
2. Štatistika. Náhodné vzorkovanie. Zobraté z: Encyclopediaeconomica.com.
3. Štatistika. Vzorkovanie. Získané z: Štatistiky.Rohož.Ubytovateľ.mx.
4. Prieskumný. Náhodné vzorkovanie. Obnovené z: prieskumného.com.
5. Moore, D. 2005. Uplatňovaná štatistika. Druhý. Vydanie.
6. Hrebeň. Náhodné vzorkovanie. Získané z: NetQuest.com.
7. Wikipedia. Štatistické vzorky. Zdroj: In.Wikipedia.orgán