Gauss-Seidel Method Vysvetlenie, aplikácie, príklady

On Metóda Gauss-Seidel Je to iteračný postup na nájdenie približných riešení systému lineárnych algebraických rovníc s ľubovoľne vybranými presnosťami. Táto metóda sa uplatňuje na štvorcové matice s nenávistnými prvkami vo svojich diagonáloch a konvergencia je zaručená, ak je matrica diagonálne dominantná.

Vytvoril ho Carl Friedrich Gauss (1777-1855), ktorý v roku 1823 urobil súkromnú demonštráciu jednému z jeho študentov. Následne ho formálne publikoval Philipp Ludwig von Seidel (1821-1896) v roku 1874, odtiaľ názov oboch matematikov.

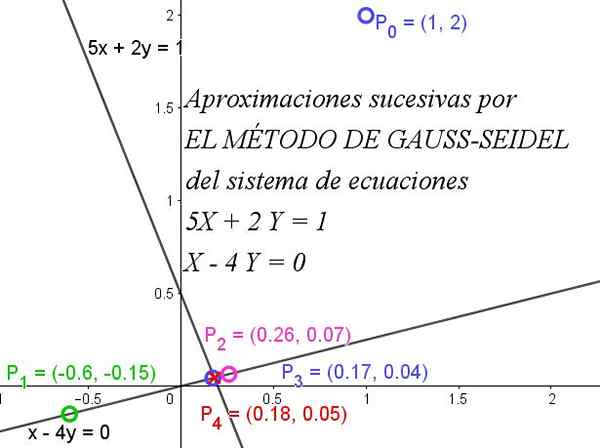
postava 1. Metóda Gauss-Seidel sa rýchlo zbieha, aby získala systém rovníc. Zdroj: f. Zapata.

Pre úplné pochopenie metódy je potrebné vedieť, že matica je diagonálne dominantná, keď je absolútna hodnota diagonálneho prvku každého riadku väčšia alebo rovná súčtu absolútnych hodnôt ostatných prvkov toho istého riadku.

Matematicky sa vyjadruje takto:

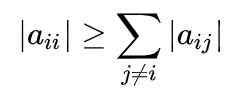
[TOC]

Vysvetlenie prostredníctvom jednoduchého prípadu

Na ilustráciu toho, čo bude metóda Gauss-Seidel mať jednoduchý prípad, v ktorom nájdete hodnoty X a Y v systéme lineárnych rovníc 2 × 2 uvedené nižšie:

5x + 2y = 1

X - 4y = 0

Kroky, ktoré chcete sledovať

1- Najprv musíte určiť, či je konvergencia bezpečná. Okamžite sa pozoruje, že v skutočnosti ide o diagonálne dominantný systém, pretože v prvom riadku má prvý koeficient väčšiu absolútnu hodnotu ako ostatné v prednom riadku:

| 5 |> | 2 |

Podobne je diagonálne dominantný aj druhý koeficient druhého riadku:

| -4 |> | 1 |

2- Premenné x a y sú jasné: 

X = (1 - 2y)/5

Y = x/4

3- Počiatočná ľubovoľná hodnota sa umiestni, nazývaná „semeno“: xo = 1, me = 2.

4

Môže vám slúžiť: odhad prostredníctvom intervalov

X1 = (1 - 2 me)/5 = (1 - 2 × 2)/5 = -3/5 

Y1 = x1 / 4 = (-3/5) / 4 = -3/20 

5- Pokračujte podobným spôsobom, aby ste získali druhú aproximáciu riešenia systému rovníc:

X2 = (1 - 2 y1)/5 = (1 - 2x (-3/20))/5 = 13/50 

Y2 = x2/4 = (13/50)/4 = 13/200

6- Tretia iterácia:

X3 = (1 - 2 y2)/5 = (1 - 2 (13/200))/5 = 87/500

Y3 = x3/4 = (87/500)/4 = 87/2000

7- Štvrtá iterácia, ako konečná iterácia tohto ilustratívneho prípadu:

X4 = (1 - 2 y3)/5 = (1 - 2 (87/2000))/5 = 913/5000

Y4 = x4/4 = (913/5000)/4 = 913/20000

Tieto hodnoty sa zhodujú celkom dobre s riešením zisteným pomocou iných metód rozlíšenia. Čitateľ to môže rýchlo skontrolovať pomocou online matematického programu.

Analýza metód

Ako je zrejmé, v metóde Gauss-Seidel sa musia približné hodnoty získané pre predchádzajúcu premennú v tom istom kroku nahradiť v nasledujúcej premennej. To ho odlišuje od iných iteračných metód, ako je Jacobi, v ktorých každý krok vyžaduje prístupy k predchádzajúcej fáze. 

Metóda Gauss-Seidel nie je paralelný postup, zatiaľ čo Gauss-Jordan je. Je to tiež dôvod, prečo má metóda Gauss-Seidel rýchlejšie konvergenčné kroky ako Jordánska metóda.

Pokiaľ ide o podmienku diagonálne dominantnej matrice, nie je to vždy spokojné. Vo väčšine prípadov však stačí vymeniť rady pôvodného systému, aby sa splnili podmienky. Okrem toho sa táto metóda takmer vždy konvertuje, aj keď nie je splnený stav diagonálnej dominancie.

Predchádzajúci výsledok, získaný štyrmi iteráciami metódy Gauss-Seidel, možno napísať desatinným spôsobom:

Môže vám slúžiť: Koľko osí symetrie má kruh?

X4 = 0,1826

Y4 = 0,04565

Presné riešenie systému zvýšených rovníc je:

X = 2/11 = 0,1818

Y = 1/22 = 0,04545.

Takže iba so 4 iteráciami sa výsledok získava s tisíckou presnosťou (0,001).

Obrázok 1 zobrazuje, ako postupné iterácie sa rýchlo konvertujú na presné riešenie.

Žiadosti

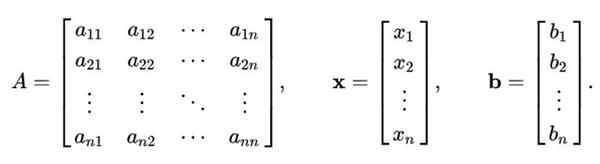
Metóda Gauss-Seidel nie je obmedzená iba na systém lineárnych rovníc 2 × 2. Vyššie uvedený postup je možné zovšeobecniť na vyriešenie lineárneho systému n rovnice s n Neznáme, ktoré sú znázornené maticly takto:

Do X = b

Kde Do Je to matica n x n, zatiaľ čo X Je to vektor n komponenty premenných, ktoré sa majú vypočítať; a b Je to vektor, ktorý obsahuje hodnoty nezávislých výrazov.

Na zovšeobecnenie sekvencie iterácií aplikovaných v ilustratívnom prípade na systém n x n, ktorý chce vypočítať premennú Xi, Bude sa uplatňovať nasledujúci vzorec:

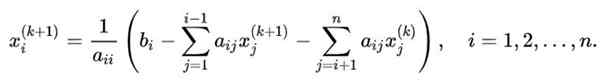
V tejto rovnici:

- klimatizovať Je to index hodnoty získanej v iterácii klimatizovať.

-K+1 Označuje novú hodnotu v nasledujúcom.

Konečný počet iterácií sa určuje, keď sa hodnota získaná v iterácii K+1 líši sa od získaných bezprostredne pred, v množstve ε, ktorá je presne požadovanou presnosťou.

Príklady metódy Gauss-Seidel

- Príklad 1

Napíšte všeobecný algoritmus, ktorý vám umožní vypočítať približný vektor riešenia X lineárneho systému NXN rovníc, vzhľadom na maticu koeficientu Do, Vektor nezávislých výrazov b, Počet iterácií (iter) a počiatočné alebo „semeno“ vektora X.

Riešenie

Algoritmus pozostáva z dvoch „pre“ cykly, jeden pre počet iterácií a druhý pre počet premenných. Bolo by to takto:

Pre k ∊ [1 ... iter]

Pre i ∊ [1… n]

X [i]: = (1/a [i, i])*(b [i] - ∑_{J = 1}ⁿ(A [i, j]*x [j]) + a [i, i]*x [i])

Môže vám slúžiť: desatinná notácia

- Príklad 2

Skontrolujte činnosť predchádzajúceho algoritmu uplatňovaním na matematický softvér Štúdio Smath zadarmo a zadarmo, k dispozícii pre Windows and Android. Zoberme si príklad matice 2 × 2, ktorá nám slúžila na ilustráciu metódy Gauss-Seidel.

Riešenie

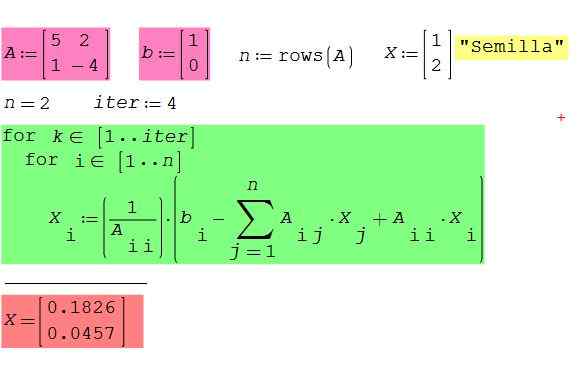Obrázok 2. Systém rovníc príkladu 2 x 2 pomocou softvéru Štúdio Smath. Zdroj: f. Zapata.

- Príklad 3

Aplikujte algoritmus Gauss-Seidel pre nasledujúci systém rovníc 3 × 3, ktorý bol predtým usporiadaný takým spôsobom, že diagonálne koeficienty sú dominantné (to znamená väčšiu absolútnu hodnotu ako absolútne hodnoty koeficientov koeficientov koeficientov rovnakého riadku):

9 x1 + 2 x2 - x3 = -2

7 x1 + 8 x2 + 5 x3 = 3

3 x1 + 4 x2 - 10 x3 = 6

Použite nulovú vektor ako semeno a zvážte päť iterácií. Komentujte výsledok.

Riešenie

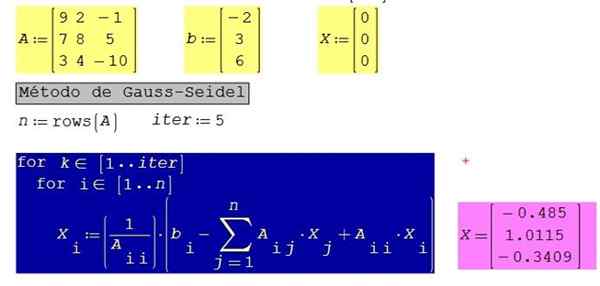Obrázok 3. Riešenie systému rovníc rozlíšeného príkladu 3 pomocou Smath Studio. Zdroj: f. Zapata.

Pre ten istý systém s 10 iteráciami namiesto 5 sa získajú nasledujúce výsledky: x1 = -0.485; X2 = 1.0123; X3 = -0.3406

To naznačuje, že stačí s piatimi iteráciami na získanie troch presných desatinných miest a že metóda rýchlo sprostredkuje roztok.

- Príklad 4

Prostredníctvom daného algoritmu Gauss-Seidel nájdete riešenie systému rovníc 4 × 4, ktorý sa vyskytuje nižšie:

10 x1 - x2 + 2 x3 + 0 x4 = 6

-1 x1 + 11 x2 - 1 x3 + 3 x4 = 25

2 x1 - 1 x2 + 10 x3 - 1 x4 = -11

0 x1 + 3 x2 - 1 x3 + 8 x4 = 15

Ak chcete začať metódu, využite toto semeno:

x1 = 0, x2 = 0, x3 = 0 a x4 = 0

Zvážte 10 iterácií a odhadnite chybu výsledku v porovnaní s iteráciou číslo 11.

Riešenie

Obrázok 4. Riešenie systému rovníc rozlíšeného príkladu 4 pomocou Smath Studio. Zdroj: f. Zapata.

Pri porovnaní s nasledujúcou iteráciou (číslo 11) je výsledok rovnaký. Najväčšie rozdiely medzi týmito dvoma iteráciami sú rádovo 2 × 10^-8, Čo znamená, že zobrazené riešenie má presnosť najmenej siedmich desatinných miest.

Odkazy

1. Metódy iteračného riešenia. Gauss-seidel. Získané z: Cimat.mx
2. Numerické metódy. Gauss-seidel. Získané z: Test.Cua.Uam.mx
3. Numeric: Gauss-Seidel Metóda. Získané z: Učte sa v Linea.vy.Edu.co
4. Wikipedia. Metóda Gauss-Seidel. Zdroj: In. Wikipedia.com
5. Wikipedia. Metóda Gauss-Seidel. Obnovené z: je.Wikipedia.com