Rovnomerné charakteristiky priameho pohybu, vzorce, cvičenia

On pohyb rovnomernej línie alebo pri konštantnej rýchlosti je taká, v ktorej sa častica pohybuje pozdĺž priamky a konštantnou rýchlosťou. Tým. Napríklad, ak za 1 sekundu cestuje 2 metre, po 2 sekundách bude 4 metre atď.

Aby bol presný opis pohybu, či už rovnomerný priamy alebo akýkoľvek iný, je potrebné stanoviť referenčný bod, ktorý sa nazýva aj nazývaný pôvod, Pokiaľ ide o to, ktoré mobilný mení pozíciu.

postava 1. Auto, ktoré sa pohybuje po priamej ceste pri konštantnej rýchlosti, má rovnomerný priamy pohyb. Zdroj: Pixabay.

Ak pohyb prechádza úplne po priamke, má tiež záujem vedieť, v akom zmysle mobilné cesty cestuje.

Na vodorovnej čiare je možné, že mobil ide doprava alebo doľava. Rozdiel medzi týmito dvoma situáciami sa robí znakmi, pričom nasledujúce je: napravo sledujem (+) a do ľavého znamenia (-).

Ak je rýchlosť konštantná, mobil nemení svoj smer ani svoj význam a tiež veľkosť jeho rýchlosti zostáva nezmenená.

[TOC]

Charakteristika

Hlavné charakteristiky rovnomerného priameho pohybu (MRU) sú nasledujúce:

-Pohyb vždy prechádza po priamke.

-Mobil s MRU prechádza rovnakými vzdialenosťami alebo priestormi v rovnakých časoch.

-Rýchlosť zostáva nezmeniteľná tak vo veľkosti aj v smere.

-MRU chýba zrýchlenie (nedochádza k zmenám rýchlosti).

-Od rýchlosti vložka Postupom času zostáva konštantný tón, Graf jeho veľkosti ako funkcia času je priamka. V príklade na obrázku 2 je čiara zelená a hodnota rýchlosti sa načíta na zvislej osi, približne +0.68 m/s.

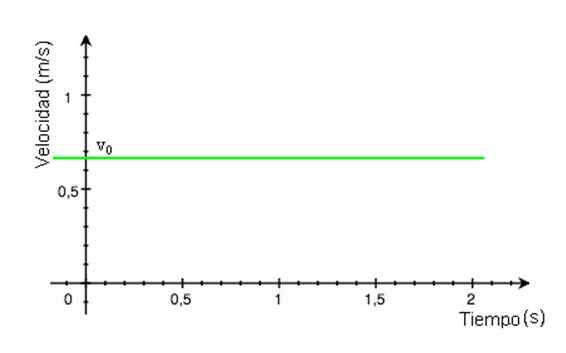Obrázok 2. Rýchlostný graf v závislosti od MRU. Zdroj: Wikimedia Commons.

-Graf polohy X vzhľadom na čas je priamka, ktorej sklon je rovnocenný s mobilnou rýchlosťou. Ak je grafový riadok X vs T horizontálny, mobil je v pokoji, ak je sklon kladný (graf obrázku 3), rýchlosť je tiež.

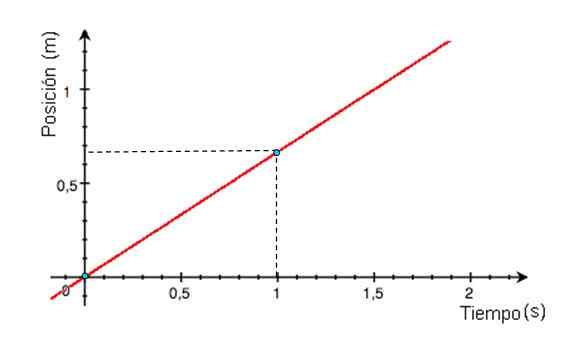Obrázok 3. Graf pozície ako funkcia času pre mobil s MRU, ktorý sa odchýlil od pôvodu. Zdroj: Wikimedia Commons.

Vzdialenosť prešla z grafu v vs. tón

Spoznajte vzdialenosť, ktorú prevezme mobil, keď je graf k dispozícii v Vs. t je veľmi jednoduché. Cesta vzdialená je rovnocenná s oblasťou pod vedením a je zahrnutá v požadovanom časovom intervale.

Môže vám slúžiť: Priemerné zrýchlenie: Ako sa vypočítava a vyrieši

Predpokladajme, že chcete poznať vzdialenosť, ktorú prešla mobilom na obrázku 2 v intervale medzi 0.5 a 1.5 sekúnd.

Táto oblasť je oblasť zatieneného obdĺžnika na obrázku 4. Vypočíta sa zistením výsledku vynásobenia základne obdĺžnika jeho výškou, ktorej hodnoty sa nachádzajú z grafiky.

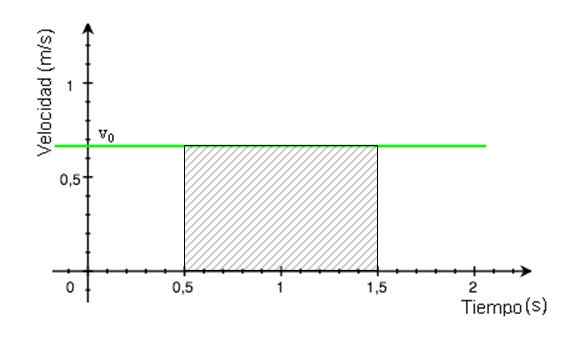Obrázok 4. Pruhovaná oblasť je rovnocenná s prevezenou vzdialenosťou. Zdroj: Upravené Wikimedia Commons.

Prejdená vzdialenosť = (1.päťdesiat.5) x 0.68 m = 0.68 m

Vzdialenosť je vždy kladné množstvo, bez ohľadu na to, či idete doprava alebo doľava.

Vzorce a rovnice

V MRU sú priemerná rýchlosť a okamžitá rýchlosť vždy rovnaká a keďže jej hodnota je sklonom grafu X vs T zodpovedajúci riadku, zodpovedajúce rovnice sú v závislosti od času nasledujúce:

-Pozícia v závislosti od času: x (t) = x_ani + VT

X_ani Predstavuje počiatočnú polohu mobilu, pri mnohých príležitostiach sa zhoduje s pôvodom referenčného systému, ale nie vždy je to takto. Táto rovnica je známa aj ako Itinerárska rovnica.

-Rýchlosť v závislosti od času: v (t) = konštanta

Keď v = 0 znamená, že mobil je odpočinok. Odpočinok je konkrétny prípad pohybu.

-Zrýchlenie ako funkcia času: A (t) = 0

V rovnomernom priamom pohybe nedochádza k zmenám rýchlosti, preto je zrýchlenie nula.

Vyriešené cvičenia

V čase riešenia cvičenia by sa malo zabezpečiť, aby situácia zodpovedala modelu, ktorý sa má použiť. Konkrétne pred použitím rovníc MRU je potrebné ubezpečiť sa, že sú použiteľné.

Nasledujúce cvičenia sú vyriešené dva mobilné problémy.

Cvičenie vyriešené 1

Dvaja športovci sa blížia k sebe s neustálym rýchlosťou 4.50 m/s a 3.5 m/s, ktoré sú spočiatku oddelené vzdialenosť 100 metrov, ako je uvedené na obrázku.

Ak si každý zachová svoju konštantnú rýchlosť, nájdite: a) ako dlho trvá stretnutie? b) Aká bude poloha každého v tom čase?

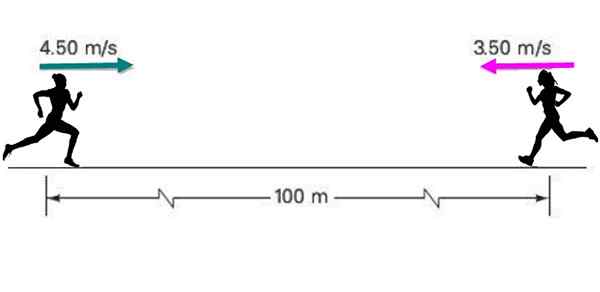Obrázok 5. Dvaja bežci sa pohybujú k sebe konštante. Zdroj: Self Made.

Riešenie

Prvým je označenie pôvodu súradníckeho systému, ktorý bude slúžiť ako referencia. Výber závisí od preferencie, že osoba, ktorá problém vyrieši.

Môže vám slúžiť: čo je objemová dilatácia? (S príkladmi)

Zvyčajne je zvolený x = 0 priamo v východiskovom bode mobilných telefónov, môže byť v bežecke ľavej alebo vpravo, môže byť zvolený v strede oboch.

a) Chystáme sa zvoliť x = 0 na bežec ľavého alebo bežec 1, preto je počiatočnou polohou v tejto oblasti x₀₁ = 0 a pre bežec 2 bude x₀₂ = 100 m. Maklér 1 sa pohybuje zľava doprava s rýchlosťou v₁ = 4.50 m/ zatiaľ čo bežec 2 to robí sprava doľava s rýchlosťou -3.50 m/s.

Pohybová rovnica pre prvého sprostredkovateľa

X₁ = x₀₁ + vložka₁tón₁ = 4.50t₁

Pohybová rovnica pre druhého sprostredkovateľa

X₂ = x₀₂ + vložka₂tón₂ = 100 -3.50t₂

Ako čas je rovnaký pre oboch tón₁ = t₂ = t , Ak bude poloha oboch rovnaká X₁ = x₂. Rovnaké:

4.50T = 100 -3.50t

Je to rovnica prvého stupňa pre čas, ktorej riešenie je t = 12.5 s.

b) Obaja bežci sú v rovnakej polohe, preto nahrádza čas získaný v predchádzajúcej časti v ktorejkoľvek z polohových rovníc. Napríklad môžeme použiť bežec 1:

X₁ = 4.50t₁ = 56.25 m

Rovnaký výsledok sa získava výmenou t = 12.5 s v rovnici polohy bežec 2.

-Cvičenie vyriešené 2

Zajac vyzýva korytnačku, aby spustila vzdialenosť 2.4 km a aby som bol spravodlivý, ponúka pol hodiny výhody. V hre korytnačka postupuje z dôvodu 0.25 m/s, čo je maximum, ktoré môže bežať. Po 30 minútach sa zajac beží rýchlosťou 2 m/s a rýchlo dosiahne korytnačku.

Po pokračovaní ďalších 15 minút si myslím, že má čas na zdriemnutie a stále vyhrať preteky, ale zaspajte 111 minút. Keď sa prebudí, beží so všetkou svojou silou, ale korytnačka už prekročila gól. Nájsť:

a) Aká výhoda vyhráva korytnačka?

b) okamih, keď zajac postupuje v korytnačke

c) okamih, keď korytnačka postupuje na zajac.

Riešenie do)

Rasa začína v t = 0. Poloha korytnačky: X_Tón = 0.25t

Pohyb zajaca má nasledujúce časti:

Môže vám slúžiť: Solárny systém: planéty, charakteristiky, pôvod, vývoj

-Odpočívaj pre výhodu, ktorú dal korytnačke: 0 < t < 30 minutos:

-Preteky, aby ste dosiahli korytnačku a po jej odovzdaní trochu behali; Celkovo sú to 15 minút pohybu.

-Spať 111 minút (odpočinok)

-Prebudiť sa príliš neskoro (šprint Konečný)

2.4 km = 2400 m

Trvanie závodu bolo: T = 2400 m/ 0.25 m/s = 9600 s = 160 minút. V tejto dobe odpočítame 111 minút od NAP a 30 výhod, čo je 19 minút (1140 sekúnd). To znamená, že bežal 15 minút pred spánkom a 4 minúty po prebudení sprintu.

V tejto dobe zajac pokrýval nasledujúcu vzdialenosť:

d_L = 2 m/s . (Pätnásť . 60 s) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Pretože celková vzdialenosť bola 2400 metrov, odčítaním obidvoch hodnôt, ukázalo sa, že zajac chýbala 120 metrov, aby dosiahla cieľ, aby dosiahla cieľ.

Riešenie b)

Poloha zajaca pred zaspaním je X_L = 2 (t - 1800), Vzhľadom na oneskorenie 30 -minúty = 1800 sekúnd. Rovná sa x_Tón a x_L Nájdeme čas, keď sú:

2 (t - 1800) = 0.25t

2T -0.25 t = 3600

T = 2057.14 s = 34.29 min

Riešenie c)

V čase, keď je zajaca pokročilý korytnačkou, ktorá spí na 1800 metrov od hry:

1800 = 0.25t

T = 7200 s = 120 minút

Žiadosti

MRU je najjednoduchší pohyb, ktorý si môžete predstaviť, a preto je prvý, ktorý sa má študovať v kinematike, ale mnoho zložitých pohybov možno opísať ako kombináciu tohto a iných jednoduchých pohybov.

Ak človek opustí svoj dom a vedie, až kým nedosiahne dlhú priamu diaľnicu, cez ktorú dlhú rýchlosť cestuje rovnakou rýchlosťou, je možné opísať jeho pohyb ako MRU, bez toho, aby sa dostal do podrobností.

Pred vstupom a opustení diaľnice samozrejme musí osoba urobiť niekoľko kôl, ale prostredníctvom použitia tohto modelu pohybu je možné odhadnúť trvanie cesty s vedomím približnej vzdialenosti medzi východiskovým bodom a bodom príchodu.

V prírode má svetlo rovnomerný priamy pohyb, ktorého rýchlosť je 300.000 km/s. Pohyb zvuku vo vzduchu sa dá predpokladať rovnomerné priamočiare s rýchlosťou 340 m/s v mnohých aplikáciách.

Pri analýze ďalších problémov, napríklad pohybu nositeľov nákladu vo vodičovi, sa prístup MRU môže použiť aj na predstavu o tom, čo sa deje v rámci vodiča.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.40-45.
2. Figueroa, D. Fyzická séria pre vedu a inžinierstvo. Zväzok 3. Vydanie. Kinematika. 69-85.
3. Giancoli, D.  Fyzika: Princípy s aplikáciami. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5^th. Edimatizovať. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Fyzika: pohľad na svet. 6^{ubytovať sa} Skrátene vydanie. Učenie sa. 15-19.
6. Wilson, J. 2011. Fyzika 10. Pearson Vzdelanie. 116-119.