Charakteristiky konvergentných šošoviek, typy a vyriešené cvičenie

Ten Konvergentné šošovky Sú to tie, ktoré sú silnejšie v ich strednej a tenšej časti na okrajoch. V dôsledku. Tento bod sa nazýva Focus alebo Image Focus a je zastúpený písmenom F. Konvergentné alebo pozitívne šošovky sa nazývajú skutočné obrazy objektov.

Typickým príkladom konvergentnej šošovky je zväčšovacie sklo. Je však bežné nájsť tento typ šošoviek na oveľa zložitejších zariadeniach, ako sú mikroskopy alebo ďalekohľad. V skutočnosti je základným zloženým mikroskopom, ktorý predstavuje dva konvergentné šošovky, ktoré majú malú ohniskovú vzdialenosť. Tieto šošovky sa nazývajú cieľový a očný.

Zväčšovacie sklo, konvergentná šošovka. 

Konvergentné šošovky sa používajú v optici pre rôzne aplikácie, aj keď možno najznámejšie je opraviť chyby v zobrazení. Preto sú naznačené, že obchodujú.

[TOC]

Charakteristika

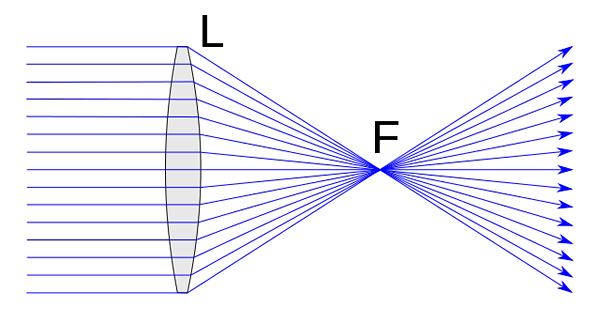Konvergentná šošovka. Chetvorno [CC0]

Konvergentné šošovky majú sériové funkcie, ktoré ich definujú. V každom prípade je možno najdôležitejšie to, čo sme už vo svojej definícii postúpili. Konvergentné šošovky sa teda vyznačujú odklonením sa zaostrením akéhokoľvek lúča, ktorý ich ovplyvňuje v smere rovnobežnom s hlavnou osou.

Okrem toho, recipročným spôsobom, akýkoľvek dopadový lúč, ktorý prechádza zameraním, sa lomuje rovnobežne s optickou osou šošovky.

Konvergentné šošovky prvky

Vzhľadom na vašu štúdiu je dôležité vedieť, ktoré prvky tvoria šošovky všeobecne a obzvlášť konvergentné šošovky.

Všeobecne sa nazýva optické centrum šošovky do bodu, v ktorom každý lúč, ktorý cez ňu prechádza, nezažije žiadnu odchýlku.

Hlavnou osou je čiara, ktorá sa spája s optickým centrom a hlavným zameraním, ktoré sme už uviedli, a ktorá je zastúpená písmenom F.

Môže vám slúžiť: Ton: Transformácie, rovnocennosti a cvičenia vyriešené

Nazýva sa hlavné zameranie na bod, v ktorom sa nachádzajú všetky lúče, ktoré ovplyvňujú objektív paralelne s hlavnou osou.

Vzdialenosť medzi optickým centrom a zaostrením sa nazýva ohnisková vzdialenosť.

Centrá zakrivenia sú definované ako centrá sfér, ktoré vytvárajú šošovku; na druhej strane, rádiá zakrivenia rádiá sféry, ktoré vedú k šošovke.

A nakoniec sa nazýva optická rovina do centrálnej roviny šošovky.

Tvorba obrázkov v konvergentných šošovkách

Vzhľadom na tvorbu obrazov v konvergentných šošovkách sa musí zohľadniť séria základných pravidiel, ktoré sú vysvetlené nižšie.

Ak lúč ovplyvňuje objektív paralelne s osou, vznikajúci lúč sa konvertuje v zaostrovacom obrázku. Ak inverzne, ak dopadajúci lúč prekročí zaostrenie objektu, blesk sa objaví v smere rovnobežnej s osou. Nakoniec sa lúče, ktoré prechádzajú optickým centrom.

V dôsledku toho v konvergentnej šošovke môžete uviesť nasledujúce situácie:

- Že objekt je umiestnený vzhľadom na optickú rovinu vo vzdialenosti väčšej ako dvojnásobok ohniskovej vzdialenosti. V takom prípade je obraz, ktorý sa vyskytuje, skutočný, obrátený a menší ako objekt.

- Že objekt je umiestnený vo vzdialenosti od optickej roviny rovnajúcej sa dvojnásobnej ohniskovej vzdialenosti. Ak sa to stane, získaný obrázok je skutočný, obrátený obrázok a rovnakú veľkosť ako objekt.

- Že objekt je vo vzdialenosti od optickej roviny medzi raz a dvojnásobkom ohniskovej vzdialenosti. Takže sa vytvára obrázok, ktorý je skutočný, obrátený a väčší ako pôvodný objekt.

- Že objekt je umiestnený vo vzdialenosti od optickej roviny nižšia ako ohnisková vzdialenosť. V takom prípade bude obrázok virtuálny, priamy a väčší ako objekt.

Môže vám slúžiť: magnetický šok: jednotky, vzorce, výpočet, príklady

Typy konvergentných šošoviek

Existujú tri rôzne typy konvergentných šošoviek: bikonvexné šošovky, šošovky planoconvexu a konvavaconvexné šošovky.

Bikonvexové šošovky, ako už názov napovedá, sa skladajú z dvoch konvexných povrchov. Medzitým majú placonvexas rovný povrch a ďalší konvexný. A nakoniec, šošovky konavaconvexu sú tvorené mierne konkávnym povrchom a ďalší konvexný.

Rozdiel s divergentnými šošovkami

Konvergentná šošovka. FIR0002 (talk) (nahrávanie) [CC BY-SA 3.0 (http: // creativeCommons.Org/licencie/By-SA/3.0/]]

Divergentné šošovky sa na druhej strane líšia od konvergentu v tom, že hrúbka klesá od okrajov smerom k stredu. Na rozdiel od toho, čo sa stalo s konvergentným, v tomto type šošoviek sú rovnobežné lúče svetla, ktoré ovplyvňujú hlavnú os. Týmto spôsobom tvoria to, čo sa nazýva virtuálne obrazy objektov.

V optike sa divergentné alebo negatívne šošovky, ako sú známe, používajú hlavne na korekciu krátkozrakosti.

Gauss rovnice tenkých šošoviek a zvýšeného objektívu

Všeobecne platí, že typ študovaných šošoviek sa nazývajú tenké šošovky. Sú definované ako tie, ktoré majú malú hrúbku v porovnaní so zakrivením povrchov, ktoré ich obmedzujú.

Tento typ šošovky je možné študovať pomocou Gaussovej rovnice a rovnici, ktorá umožňuje určiť zvýšenie šošovky.

Gaussová rovnica

Gaussova rovnica tenkých šošoviek slúži na vyriešenie množstva základných problémov s optikou. Preto je to veľký význam. Váš výraz je nasledujúci:

1/f = 1/p +1/q

Kde 1/ f sa nazýva sila šošovky a F je ohnisková vzdialenosť alebo vzdialenosť od optického centra k Focamu. Jednotkou merania výkonu šošovky je diopter (d), ktorá je 1 d = 1 m^-1. Pokiaľ ide o svoju časť, P a Q sú vzdialenosť, pri ktorej je objekt a vzdialenosť, ku ktorej je pozorovaný jeho obraz.

Môže vám slúžiť: Teória veľkého tresku: Charakteristiky, fázy, dôkazy, problémy

Zvýšená šošovka

Bočné zvýšenie tenkej šošovky sa získa s nasledujúcou expresiou:

M = - q / p

Kde m je nárast. Z hodnoty zvýšenia je možné odvodiť sériu dôsledkov:

Áno | M | > 1, veľkosť obrázka je väčšia ako veľkosť objektu

Áno | M | < 1, el tamaño de la imagen es menor que el del objeto

Ak m> 0, obrázok je vpravo a na rovnakej strane objektívu ako objekt (virtuálny obrázok)

Áno m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Cvičenie

Telo sa nachádza o meter od konvergentnej šošovky, ktorá má ohniskovú vzdialenosť 0, 5 metrov. Aký bude obraz tela? Ako ďaleko nájdete?

Máme nasledujúce údaje: p = 1 m; F = 0,5 m.

Tieto hodnoty nahrádzame v Gaussovej rovnici tenkých šošoviek:

1/f = 1/p +1/q

A zostáva nasledujúce:

1/0,5 = 1 + 1/q; 2 = 1 + 1/q

Vyčistime 1/q

1/q = 1

Potom vyčistiť Q a získať:

Q = 1

Odtiaľ nahradíme rovnicu zvýšenia šošovky:

M = -q / p = -1 / 1 = -1

Preto je obrázok skutočný od Q> 0, invertovaný, pretože m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Odkazy

1. Svetlo (n.d.). Na Wikipédii. Z toho sa z toho 18. marca 2019.Wikipedia.orgán.
2. Lekner, John (1987). Teória reflexie, elektromagnetických a partelových vĺn. Prubár.
3. Svetlo (n.d.). Na Wikipédii. Získané 20. marca 2019 z.Wikipedia.orgán.
4. Objektív (n.d.). Na Wikipédii. Z toho sa z toho 17. marca 2019.Wikipedia.orgán.
5. Objektív (optika). Na Wikipédii. Získané 19. marca 2019 z.Wikipedia.orgán.
6. Acts, Eugene (2002). Optika (4. vydanie.). Addison Wesley.
7. Tupler, Paul Allen (1994). Fyzický. 3. vydanie. Barcelona: obrátil som sa.