Gravicentro

Aká je daň?

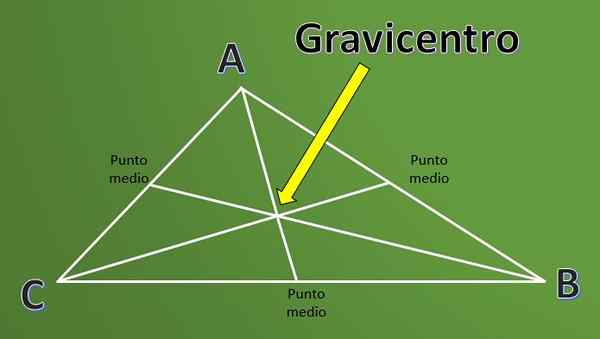
On Gravicentro Je to definícia, ktorá sa široko používa v geometrii pri práci s trojuholníkmi. Aby sme pochopili definíciu Gravicentra, je potrebné najprv poznať definíciu „média“ trojuholníka.

Mediány trojuholníka sú segmenty čiary, ktoré začínajú v každom vrchole a dosahujú strednú stranu opačnej strany k uvedenému vrcholu.

Priesečný bod troch mediánov trojuholníka sa nazýva baricentro alebo sa nazýva aj zdaňovanie. Nestačí len poznať definíciu, je zaujímavé vedieť, ako sa tento bod vypočíta.

Výpočet baricentra

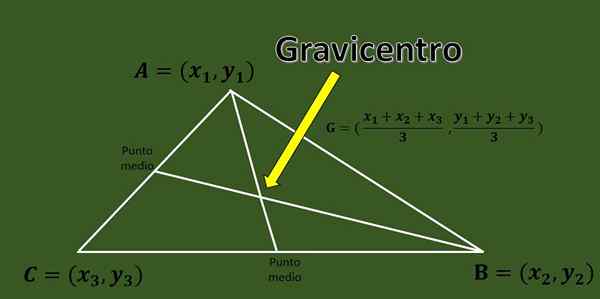
Vzhľadom na trojuholník ABC s vrcholmi a = (x1, y1), b = (x2, y2) a c = (x3, y3), gravicentro je priesečník troch mediánov trojuholníka trojuholníka.

Rýchly vzorec, ktorý umožňuje výpočet zdaňovania trojuholníka, súradnice jeho vrcholov sú známe:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

S týmto vzorcom môžete poznať umiestnenie gravicentra v karteziánskej rovine.

Charakteristika dane

Nie je potrebné sledovať tri mediány trojuholníka, pretože pri kreslení dvoch z nich sa preukáže, ak je zdanenie.

Zdaňovanie rozdeľuje každú medián na 2 časti, ktorých podiel je 2: 1, to znamená, že dva segmenty každého mediánu sú rozdelené do segmentov dĺžok 2/3 a 1/3 celkovej dĺžky, tým väčšia vzdialenosť je taká Čo je medzi vrcholom a letákom.

Nasledujúci obrázok ilustruje túto vlastnosť lepšie.

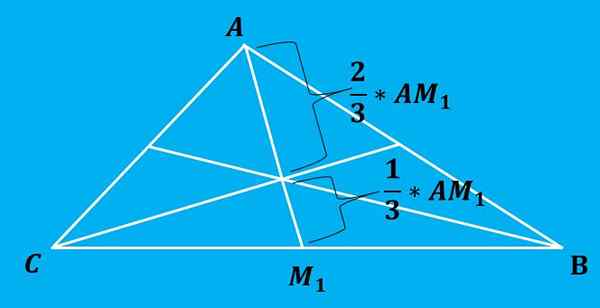
Vzorec na výpočet zdaňovania je veľmi jednoduchý. Spôsob, ako získať tento vzorec, je výpočet priamych rovníc, ktoré každá medián definuje, a potom nájsť bod rezania týchto čiar.

Cvičenia

Nižšie je uvedený malý zoznam problémov pri výpočte baricentra.

1.- Vzhľadom na trojuholník vrcholov a = (0,0), b = (1,0) a c = (1,1), vypočítajte zdaňovanie uvedeného trojuholníka.

Pomocou daného vzorca sa dá rýchlo dospieť k záveru, že gravicentro trojuholníka ABC je:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Ak má trojuholník vrcholy a = (0,0), b = (1,0) a c = (1/2,1), aké sú súradnice zdanenia?

Pretože sú známe vrcholy trojuholníka, uplatňuje sa vzorec výpočtu zdanenia. Gravicentro má preto súradnice:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Vypočítajte možných daňovníkov pre rovnostranný trojuholník tak, aby dva z jeho vrcholov boli a = (0,0) a b = (2,0).

V tomto cvičení sú špecifikované iba dva vrcholy trojuholníka. Aby sa našli možné gravicentre, tretí vrchol trojuholníka musí najskôr vypočítať.

Pretože trojuholník je rovnostranný a vzdialenosť medzi A a B je 2, tretí vrchol C musí byť vo vzdialenosti 2 A a B.

Použitím skutočnosti, že v rovnostrannom trojuholníku sa výška zhoduje s mediánom a tiež s použitím vety Pythagoras je možné dospieť k záveru, že možnosti pre súradnice tretieho vrcholu sú C1 = (1, √3) alebo C2 = (1, - - - √3).

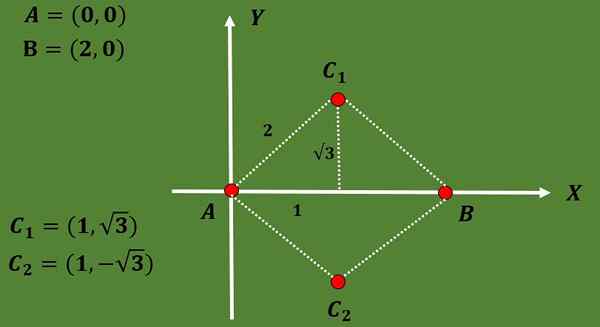
Takže súradnice týchto dvoch možných gravicentrov sú:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -štvrté)/3) = (3/3, -√3/3) = (1, -√3/3).

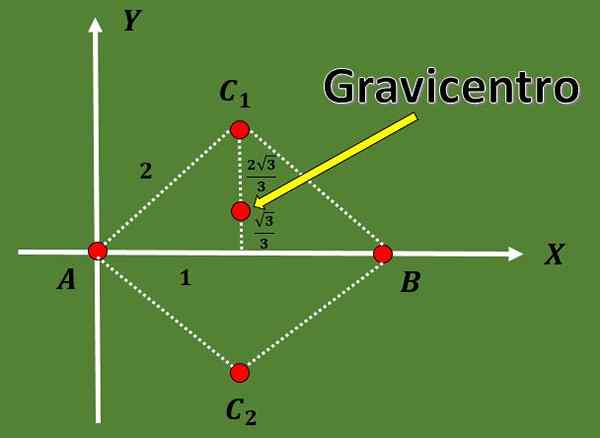
Vďaka predchádzajúcim účtom je možné poznamenať, že medián je rozdelený na dve časti, ktorých podiel je 2: 1.