Homografická funkcia Ako graf, vyriešené cvičenia

Ten funkciaHomografický alebo racionálny Je to typ matematickej funkcie zloženej z delenia dvoch polynomických komponentov. Poskytuje formulár p (x)/q (x), kde q (x) nemôže mať nulové tvary.

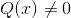
Napríklad výraz (2x - 1)/(x + 3) zodpovedá homografickej funkcii s p (x) = 2x - 1 y q (x) = x + 3.

Zdroj: Pixabay.com

Homografické funkcie tvoria časť štúdie analytických funkcií, ktorá sa lieči z grafického prístupu a zo štúdie domény a rozsahu. Je to kvôli obmedzeniam a základom, ktoré sa musia uplatňovať na ich uznesenia.

[TOC]

Čo je to homografická funkcia?

Sú to racionálne výrazy jedinečnej premennej, aj keď to neznamená, že neexistuje žiadny podobný výraz pre dve alebo viac premenných, kde by už bol v prítomnosti telies vo vesmíre, ktoré sa riadia rovnakými vzormi ako homografická funkcia na úrovni.

V niektorých prípadoch majú skutočné korene, ale existencia vertikálnych a horizontálnych asymptotov sa vždy zachováva, ako aj rast a znižovanie intervalov. Zvyčajne je prítomný iba jeden z týchto trendov, ale existujú výrazy, ktoré sú schopné ukázať oboje vo svojom vývoji.

Jeho doména je obmedzená koreňmi menovateľa, pretože neexistuje rozdelenie medzi nula reálnych čísel.

Zmiešaná homografická funkcia

Pri výpočte sú veľmi časté, najmä diferenciálne a komplexné, sú potrebné na odvodenie a anti -angel pod konkrétnymi vzorcami. Niektoré z najbežnejších sú klasifikované nižšie.

Nth Pár homografickej funkcie

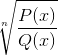
Vylučuje všetky prvky domény, ktoré spôsobujú negatívny argument. Korene prítomné v každom polynóme ukazujú nulové hodnoty pri vyhodnotení.

Tieto hodnoty sú akceptované radikálnymi, aj keď by sa malo zvážiť základné obmedzenie homografickej funkcie. Kde q (x) nemôže prijímať nulové hodnoty.

Môže vám slúžiť: Transcendentné funkcie: typy, definícia, vlastnosti, príklady

Musia byť zachytené riešenia intervalov:

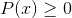
Na dosiahnutie križovatiek sa môže použiť okrem iného metóda znaku.

Logaritmus homografickej funkcie

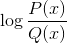
Vylučuje hodnoty domény, ktoré hádzajú negatívne intervaly a nuly. Pretože nuly sú už vylúčené z menovateľa, riešenia: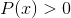

Je tiež bežné nájsť oba výrazy v jednom, okrem iných možných kombinácií.

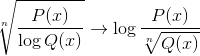
Ako grafovať homografickú funkciu?

Homografické funkcie graficky zodpovedajú hyperbolasom v rovine. Ktoré sa prepravujú vodorovne a vertikálne podľa hodnôt, ktoré definujú polynómy.

Existuje niekoľko prvkov, ktoré musíme definovať, aby sme grafovali racionálnu alebo homografickú funkciu.

Nehnuteľnosť

Prvým budú korene alebo nuly funkcií P a Q.

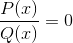
Dosiahnuté hodnoty budú označené na osi x grafiky. Označujúce križovatky grafu s osou.

Vertikálny asymptot

Zodpovedajú vertikálnym čiar, ktoré vymedzujú graf podľa trendov, ktoré prezentujú. Dotknú sa osi X v hodnotách, ktoré spôsobujú nominátor nuly a nikdy sa nedotknú grafom homografickej funkcie.

Horizontálny asymptot

Predstavovaný vodorovnou čiarou pre steh, vymedzil limit, pre ktorý nebude funkcia definovaná v presnom bode. Trendy budú pozorované pred a po tomto riadku.

Na jeho výpočet sa musíme uchýliť k metóde podobnej metóde L'Hopital, ktorá sa používa na riešenie racionálnych funkcií, ktoré majú tendenciu nekonečno. Musia sa vziať koeficienty najvyšších mocností v čitateľovi a menovateľovi funkcie.

Napríklad nasledujúci výraz má horizontálny asymptot pri y = 2/1 = 2.

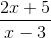
Interval rastu

Hodnoty usporiadaného budú mať v grafe trendy v dôsledku asymptotov. V prípade rastu sa funkcia zvýši z hodnôt, keď sa hodnotia prvky domény zľava doprava.

Môže vám slúžiť: 60 deliteľov

Klesajúci interval

Usporiadané hodnoty sa znížia, keď sa hodnotia prvky domény zľava doprava.

Skoky nájdené v hodnotách sa nezohľadnia, keď sa zvyšuje alebo klesá. K tomu dôjde, keď je graf blízko vertikálneho alebo horizontu.

Križovatka s y

Nula hodnota x, je priesečník s osou súradnicov. Toto je veľmi užitočná skutočnosť na získanie grafu racionálnej funkcie.

Príklady

Definujte graf nasledujúcich výrazov, nájdite jeho korene, vertikálne a horizontálne asymptoty, rast a intervaly zníženia a priesečník s osou usporiadaného.

Cvičenie 1

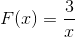
Výraz nemá korene, pretože v čitateľovi má konštantnú hodnotu. Obmedzenie, ktoré sa má použiť, bude x odlišné od nuly. S horizontálnym asymptotom pri y = 0 a asymptote vertikálne pri x = 0. Neexistujú žiadne križovatky s osou a.

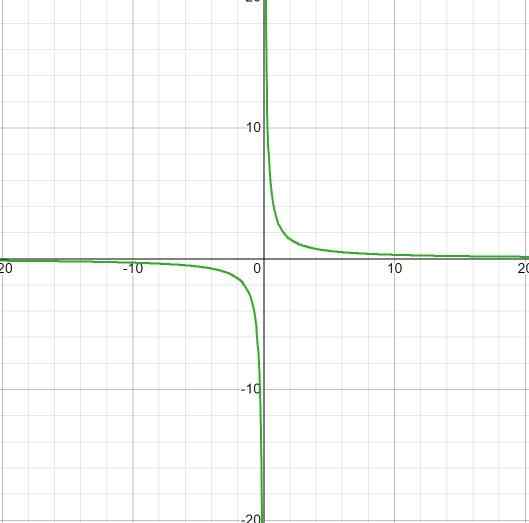
Zistilo sa, že neexistujú žiadne intervaly rastu ani s skokom z menej na nekonečné v x = 0.

Interval zníženia je

ID: (-∞; o) u (0, ∞)

Cvičenie 1.2

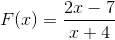
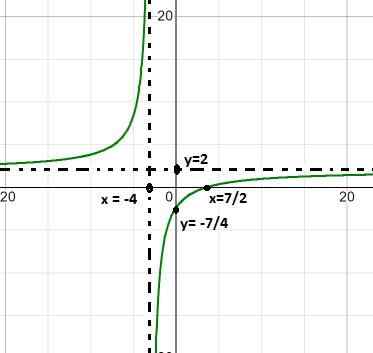
2 polynómy sa pozorujú ako v počiatočnej definícii, takže postupujeme podľa stanovených krokov.

Zistený koreň je x = 7/2, ktorý je výsledkom vyrovnania funkcie.

Vertikálny asymptot je v x = - 4, čo je hodnota vylúčená z domény kvôli stavu racionálnej funkcie.

Horizontálny asymptot je v y = 2, to po delení 2/1, koeficienty premenných 1. stupňa 1.

Má križovatku s tými, ktoré sú usporiadané na y = - 7/4. Hodnota nájdená po vyrovnávaní x na nulu.

Môže vám slúžiť: frakcia ekvivalentná 3/5 (riešenie a vysvetlenie)

Funkcia rastie neustále, s skokom z viac na menej nekonečné okolo koreňa x = -4.

Jeho interval rastu je (-∞, - 4) u ( - 4, ∞).

Ak je hodnota x blízko k menej nekonečnej, funkcia má hodnoty blízko 2. To isté sa stane, keď sa X blíži nekonečnejšie.

Expresia sa blíži nekonečnejšie, keď sa hodnotí v - 4 vľavo a menej nekonečné, keď sa hodnotí v - 4 vpravo.

Cvičenie 2

Pozoruje sa graf nasledujúcej homografickej funkcie:

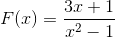
Opíšte ich správanie, korene, vertikálne a horizontálne asymptoty, rast a zníženie intervalov a priesečník s usporiadanou osou.

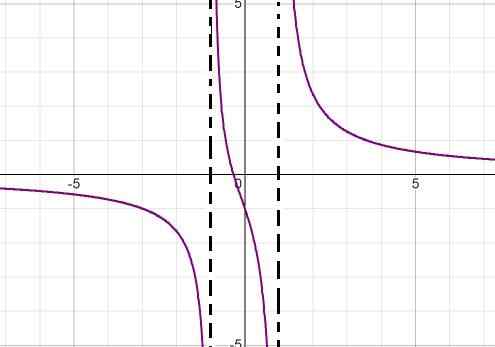
Menovateľ expresie indikuje faktorovanie rozdielu štvorcov (x + 1) (x - 1) hodnoty koreňov. Týmto spôsobom možno obe vertikálne asymptoty definovať ako:

x = -1 a x = 1

Horizontálny asymptot zodpovedá osi Abscissa, pretože hlavná sila je v menovateľovi.

Jeho jediný koreň je definovaný x = -1/3.

Výraz sa vždy znižuje zľava doprava. Priblíži sa k nule, keď má tendenciu k nekonečnu. Menej nekonečne, keď sa blíži -1 vľavo. Nekonečnejšie, keď sa blíži -1 napravo. Menej nekonečné, keď sa priblížime 1 vľavo a viac nekonečno, keď sa priblížite 1 vpravo.

Odkazy

1. Aproximácia s racionálnymi funkciami. Donald J. Nový človek. American Matematical Soc., 31. decembra. 1979
2. Ortogonálne hodnotiace funkcie. University of La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13. februára. 1999
3. Hodnotenie aproximácie skutočných funkcií. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. marca. 2011
4. Algebraické funkcie. Gilbert Ames Bliss. Couer Corporation, 1. januára. 2004
5. Španielska matematická spoločnosť časopis, 5-6 zväzkov. Španielska matematická spoločnosť, Madrid 1916