Typy trenia, koeficient, výpočet, cvičenia

Ten trenie Je to odpor voči posunu jedného povrchu, keď je v kontakte s druhým. Je to povrchový jav, ktorý sa vyskytuje medzi tuhými, tekutými a plynnými materiálmi. Tangenciálna odporová sila na dva povrchy v kontakte, ktoré sú proti smeru relatívneho posunu medzi týmito povrchmi, sa tiež nazýva trecia sila alebo trecia sila F_r.

Na vytlačenie pevného tela na povrchu sa musí aplikovať vonkajšia sila, ktorá dokáže prekonať trenie. Keď sa telo pohybuje, trecia sila pôsobí na telo a znižuje jeho rýchlosť a môže ju dokonca zastaviť.

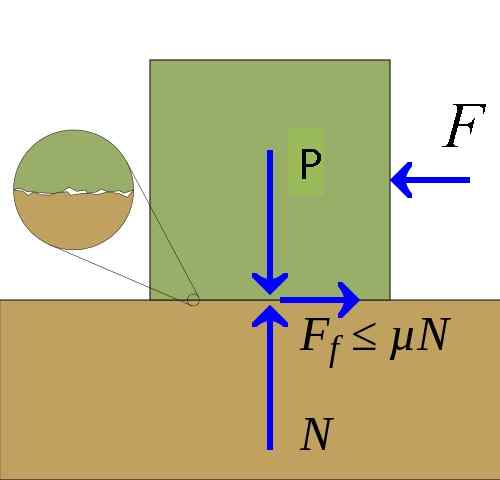
Trenie [autor Keta, Pietter Kuiper (https: // commons.Wikimedia.org/wiki/súbor: trenie.Svg)]

Trečná sila môže byť graficky reprezentovaná pomocou diagramu síl tela v kontakte s povrchom. V tomto diagrame trecia sila F_r Je nakreslená zložkou sily aplikovanej na tangenciálne telo na povrch.

Kontaktný povrch vyvíja reakčnú silu na telo nazývané normálna sila N. V niektorých prípadoch je normálna sila iba spôsobená hmotnosťou P tela, ktoré spočíva na povrchu av iných prípadoch.

Trenie pochádza z toho, že medzi povrchmi v kontakte sú mikroskopické rugá. Keď sa pokúsite presunúť jeden povrch na druhom. Straty energie sa vyrábajú vo forme tepla, ktorá sa nepoužíva na pohyb tela.

[TOC]

Typy trenia

Existujú dva hlavné typy trenia: trenie Coulomblom o Suché trenie a tekuté trenie.

-Trenie

Trenie Coulomblom Vždy je proti pohybu tiel a je rozdelený na dva typy trenia: statické trenie a kinetické (alebo dynamické) trenie.

V statickom trení nie je pohyb tela na povrchu. Aplikovaná sila je veľmi nízka a nestačí na prekonanie trecej sily. Trenie má maximálnu hodnotu, ktorá je úmerná normálnej sile a nazýva sa statická trecia sila F_rekrea.

Statická trecia sila je definovaná ako maximálna sila, ktorá odoláva na začiatku pohybu tela. Ak použitá sila prekročí statickú treckú silu, zostáva na svojej maximálnej hodnote.

Kinetické trenie pôsobí, keď je telo v pohybe. Sila potrebná na udržanie tela s trením sa nazýva kinetická trecia sila F_Rc.

Sila kinetického trecie.

Zákony o trení Coulomb

1. Trečná sila je priamo úmerná normálnej sile k kontaktnému povrchu. Konštanta proporcionality je koeficient trenia μ ktorá existuje medzi povrchmi v kontakte.
2. Trecia sila je nezávislá od veľkosti zjavnej kontaktnej plochy medzi povrchmi.
3. Kinetická trecia sila je nezávislá od rýchlosti kĺzania tela.

-Trenie

Trenie sa tiež vyskytuje, keď sa telá pohybujú v kontakte s tekutými alebo plynnými materiálmi. Tento typ trenia sa nazýva trenie tekutiny a je definovaný ako odolnosť voči pohybu telies v kontakte s tekutinou.

Môže vám slúžiť: ľahké experimenty fyziky (primárna univerzita)

Trvanie tekutín sa tiež týka odporu tekutiny na tok v kontakte s tekutými vrstvami toho istého materiálu alebo iného a závisí od rýchlosti a viskozity tekutiny. Viskozita je miera odporu voči pohybu tekutiny.

-Trenie

Trenie Stokes je typ tekutého trenia, v ktorom sférické častice ponorené do viskóznej tekutiny, v laminárnom toku, zažívajú treniacu silu, ktorá spomaľuje jej pohyb v dôsledku kolísania molekúl tekutiny.

Stokes Trecie [autor: Kraiennest (https: // commons.Wikimedia.org/wiki/súbor: Stokes_sphere.Svg)]

Prietok je laminárny, keď sú viskózne sily, ktoré sú proti pohybu tekutiny, väčšie ako zotrvačné sily a tekutina sa pohybuje s dostatočne malou rýchlosťou a v rektilineárnej trajektórii.

Koeficienty trenia

Podľa prvého zákona o trení Coulomblom Koeficient trenia μ Získava sa zo vzťahu medzi trecou silou a normálnou silou na kontaktný povrch.

μ = f_r/N

Koeficient μ Je to bezrozmerné množstvo, pretože ide o vzťah medzi dvoma silami, ktorý závisí od povahy a spracovania materiálov v kontakte. Všeobecne je hodnota koeficientu trenia medzi 0 a 1.

Koeficient statického trenia

Statický koeficient trenia je konštanta proporcionality, ktorá existuje medzi silou, ktorá bráni pohybu tela v stave kontaktu na kontaktnom povrchu a normálnou silou k povrchu.

μ_a= F_rekrea/N

Koeficient kinetického trenia

Koeficient kinetického trenia je konštanta proporcionality, ktorá existuje medzi silou, ktorá obmedzuje pohyb tela, ktorý sa pohybuje na povrchu a normálna sila na povrch.

μ_c= F_Rc/N

Statický koeficient trenia je väčší ako koeficient kinetického trenia.

μ_S> μ_c

Koeficient elastického trenia

Koeficient elastického trenia je odvodený z trenia medzi kontaktnými povrchmi elastických, mäkkých alebo hrubých materiálov, ktoré sú deformované aplikovanými silami. Trenie je proti relatívnemu pohybu medzi dvoma elastickými povrchmi a posunom je sprevádzaný elastickou deformáciou povrchových vrstiev materiálu.

Koeficient trenia získaného za týchto podmienok závisí od stupňa drsnosti povrchu, od fyzikálnych vlastností kontaktných materiálov a veľkosti tangenciálnej zložky počutej sily v rozhraní materiálu.

Koeficient molekulárneho trenia

Koeficient molekulárneho trenia sa získa zo sily, ktorá obmedzuje pohyb častíc, ktorá sa posúva po mäkkom povrchu alebo cez tekutinu.

Ako sa vypočíta trenie?

Trečná sila v tuhých rozhraniach sa vypočíta pomocou rovnice F_r = μn

N Je to normálna sila a μ Je to koeficient trenia.

V niektorých prípadoch sa normálna sila rovná hmotnosti tela P. Hmotnosť sa získa vynásobením hmotnosti m tela v dôsledku zrýchlenia gravitácie g.

P= mg

Nahradením hmotnostnej rovnice v rovnici trecej sily sa získa:

Môže vám slúžiť: Priemerné zrýchlenie: Ako sa vypočítava a vyrieši

F_r = μmg

Normálne charakteristiky

Ak je objekt v pokoji na rovnom povrchu, normálna sila je to, čo vyvíja povrch na tele a je proti sile kvôli gravitácii, podľa Newtonovho zákona o konaní a reakcii.

Normálna sila vždy pôsobí kolmá na povrch. Na naklonenom povrchu sa normálny znižuje so zvyšujúcim sa uhlom sklonu a body v kolmom smere od povrchu, zatiaľ čo hmotnosť vertikálne smeruje dole nadol. Rovnica normálnej sily na naklonenom povrchu je:

N = mgcosθ

9 = uhol sklonu kontaktnej plochy.

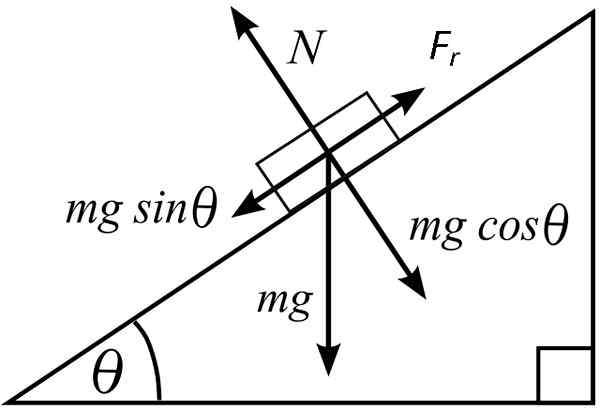Trenie v sklonenej rovine [podľa MetS501 (https: // commons.Wikimedia.org/wiki/file: free_body.Svg)]

Zložka sily pôsobiacej na telo na posúvanie je:

F = mgsenθ

Keďže sa aplikovaná sila zvyšuje na maximálnu hodnotu trenia, táto hodnota zodpovedá statickej trecej sile. Kedy  F = f_rekrea, Statická trecia sila je:

F_rekrea= mgsenθ

A statický koeficient trenia sa získava dotyčnom uhlovi sklonu θ.

μ_a = tank

Vyriešené cvičenia

-Trecia sila objektu, ktorý spočíva na vodorovnom povrchu

Krabica 15 kg umiestnená na vodorovnom povrchu je tlačená osobou, ktorá aplikuje silu 50 Newtona pozdĺž povrchu, aby sa pohybovala, a potom naneste silu 25 N, aby udržala box v pohybe konštantnou rýchlosťou. Určovať statické a kinetické koeficienty trenia.

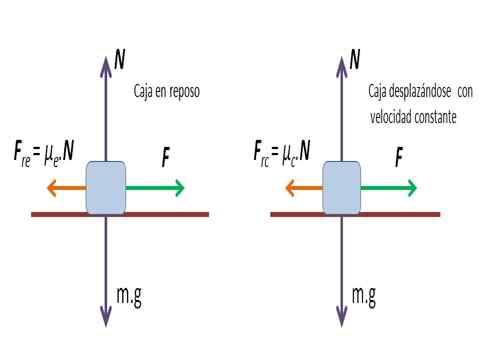Box pohybujúci sa na horizontálnom povrchu

Riešenie: S hodnotou aplikovanej sily na presun boxu sa získa koeficient statického trenia μ_a.

μ_a= F_rekrea/N

Normálna sila N na povrch sa rovná hmotnosti škatule, takže N = m.g

N = 15 kgx9,8 m/s²

N = 147New

V tomto prípade, μ_a= 50New/147New

μ_a= 0,34

Aplikovaná sila na udržanie rýchlosti konštantného boxu je kinetická trenie, ktorá sa rovná 25New.

Kinetický koeficient trenia sa získava pomocou rovnice μ_c= F_Rc /N

μ_c= 25New/147New

μ_c= 0,17

-Trecia sila objektu pod pôsobením sily s uhlom sklonu

Muž aplikuje silu na krabicu 20 kg s uhlom aplikačného uhla 30 ° vo vzťahu k povrchu, kde spočíva. Aká je veľkosť aplikovanej sily na presun škatule, ak je koeficient trenia medzi škatuľou a povrchom 0,5?

Riešenie: Aplikovaná sila a jej vertikálne a horizontálne komponenty sú znázornené v diagrame voľného tela.

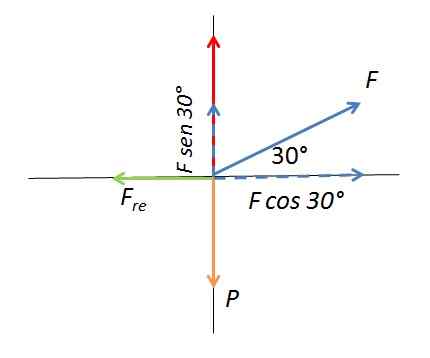Diagram voľného tela

Aplikovaná sila tvorí uhol 30 ° s vodorovným povrchom. Vertikálna zložka sily zvyšuje normálnu silu ovplyvňujúcu statickú trennú silu. Box sa pohybuje, keď horizontálna zložka aplikovanej sily presahuje maximálnu hodnotu trecej sily F_rekrea. Zodpovedaním horizontálnej zložky sily so statickým trením sa získa:

F_rekrea = Fcosθ                       [1]

F_rekrea= μ_a.N                          [2]

Môže vám slúžiť: Rutherford Atomic Model: História, experimenty, postuláty

μ_a.N = fcosθ                      [3]

Normálna sila

Normálna sila už nie je hmotnosť tela v dôsledku vertikálnej zložky sily.

Podľa Newtonovho druhého zákona je súčet síl pôsobiacich na škatuli na vertikálnej osi prázdny, preto je vertikálnou súčasťou zrýchlenia do_a= 0. Normálna sila sa získava zo súčtu

F sen30 ° + n - p = 0                      [4]

P = m.g                                        [5]

F SNN 30 ° + n - M.G = 0                [6]

N = m.G - f sen 30 °                      [7]

Pri výmene rovnice [7] v rovnici [3] sa získa toto:

μ_a. (m.G - f sin 30 °) = fcos30 °     [8]

Vyčistí sa F Z rovnice [8] a získané:

F = μ_a . m.G /(cos 30 ° + μ_a Sin 30 °) = 0,5 x 20 kg x 9,8 m/s² / (0,87+ (0,5 x 0,5)) =

F = 87,5New

-Trenie v pohyblivom vozidle

Vozidlo 1,5 ton sa pohybuje na priamej a horizontálnej ceste rýchlosťou 70 km/h. Vodič vizualizuje v určitej vzdialenosti prekážky na ceste, ktoré ho nútia ostro zastaviť. Po zastavení vozidla korčule na krátku dobu, kým sa nezastaví. Ak je koeficient trenia medzi pneumatikami a cestou 0,7; Určite nasledujúce:

1. Aká je hodnota trenia, zatiaľ čo vozidlo patiny?
2. Spomalenie vozidla
3. Vzdialenosť prevezená vozidlom od zastávok, až kým sa nezastaví.

Riešenie:

Oddiel a

Diagram voľného tela ukazuje sily pôsobiace na vozidlo pri korčuľovaní.

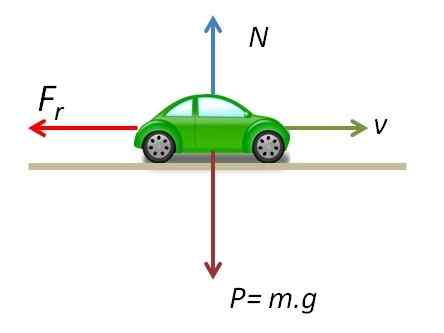Sily pôsobiace v pohyblivom vozidle

Pretože súčet síl pôsobiacich vo vertikálnej osi je nula, normálna sila sa rovná hmotnosti vozidla.

N = m.g

M = 1,5 ton = 1500 kg

N = 1500 kgx9,8 m/s²= 14700New

Trecia sila vozidla pri korčuľovaní je:

F_r = μn = 0,7 x 14700New

= 10290 NOVÝ

Oddiel B

Trečná sila ovplyvňuje zníženie rýchlosti vozidla pri korčuľovaní.

Pri uplatňovaní Newtonovho druhého zákona sa hodnota spomalenia získa vymazaním rovnice F = m.do

A = f/m

A = (-10290 nových)/ 1500 kg

= -6,86 m/s²

Oddiel C

Počiatočná rýchlosť vozidla je vložka₀ = 70 km/h = 19,44 m/s

Keď vozidlo zastaví svoju konečnú rýchlosť, je to vložka_F = 0 A spomalenie je a = -6,86 m/s²

Vzdialenosť prevezená vozidlom, pretože sa zastaví, až kým sa nezastaví, získa sa zúčtovaním d z nasledujúcej rovnice:

vložka_F² = v₀²+2AD

D = (v_F² - vložka₀²)/2a

= ((0)²-(19,44 m/s)²)/(2x (-6,86 m/s²)

D = 27,54 m

Vozidlo cestuje 27,54 m vzdialenosť pred zastavením.

 Odkazy

1. Výpočty koeficientu trenia za elastických kontaktných podmienok. Mikhin, n m. 2, 1968, Soviet Materials Science, zv. 4, p. 149-152.
2. Blau, p j. Veda a technológia trenia. Florida, USA: CRC Press, 2009.
3. Vzťah medzi adhéziou a trením. Isralachvili, J n, Chen, You-Lung a Yoshizawa, H. 11, 1994, Journal of Adhession Science and Technology, zv. 8 str. 1231-1249.
4. Zimba, J. Sila. Baltimore, Maryland: The Johns Hopkins University Press, 2009.
5. Bhushan, b. Princípy a aplikácie Trilogy. New York: John Wiley a Sons, 1999.
6. Sharma, C S a Purohit, K. Teória mechanizmov a strojov. Nové Dillí: Prentice Hall of India, 2006.