Balenie

Faktor balenia je frakcia, ktorá naznačuje, aký objem častice zaberajú, či už atómy, ióny alebo molekuly, vo vnútornom priestore kryštálu. Jeho hodnota je vždy menšia ako 1, čo sa stáva 100% objemu skla; Presnejšie povedané, jej jednotná bunka, ktorá je najmenším znázornením celého skla.

100% faktor balenia znamená, že častice zaberajú objem jednotnej bunky v celom rozsahu. Fyzicky nie je možné, aby sa to stalo, pretože by to znamenalo napríklad, že atómy deformujú svoje rádiá a rozpúšťajú sa, akoby boli „elektronickou kvapalinou“. Geometria atómov, sférická pre pohodlie, vždy vedie k prázdnym priestorom počas balenia.

Ako sa to stáva v sladkých výdajných strojoch, faktor balenia nám hovorí, aké „tesné“ sú častice kryštálu: čím väčšie je, tým viac ďasien alebo atómov bude vo vesmíre

V definícii faktora obalu sa predpokladá, že atómy pozostávajú z tuhých guľôčok, ako sú ďasná alebo gule cukrovinky z daného stroja (vynikajúci obraz). Medzi guľami budú vždy duté priestory, kde sa dajú prepašovať menšie gule (nečistoty alebo prísady).

Ak zvýšime faktor balenia, gule sa stlačia a otáčajú najkompaktnejšie a najhustejšie sklo; Alebo na druhej strane, deformovateľnejšie, rovnako ako s kravskými a ťažnými kovmi.

Balenie sa vzťahuje na akýkoľvek typ skla. Jeho výpočet sa však môže stať trochu únavným, takže sa bude brať do úvahy iba pre atómové kryštály s jednoduchými štruktúrami.

[TOC]

Balenie

Faktor balenie sa zvyčajne vyjadruje ako percentuálny podiel. Napríklad, ak je jeho hodnota 40%, znamená to, že častice sotva zaberajú 40% celkového priestoru jednotkovej bunky; Alebo to, čo je to isté ako uvádzanie, že 60% skla je „prázdne“.

Vyššie uvedené objasňuje, aký je vzorec na výpočet tohto faktora:

• Škaredý = (objem atómov)/ (objem jednotkovej bunky)

Kde škaredé znamená Atómový balenie, Aké sú najjednoduchšie kryštály.

Objem jednotkovej bunky závisí od jej parametrov (ako je dĺžka jej bokov), s ktorými sa prebieha jednoduchou geometriou na výpočet jej objemu. Na druhej strane atómy sú tie, ktoré definujú bunku, takže je možné vyjadriť ich rozmery z atómových rádií, ako bude vidieť v nasledujúcich častiach.

Môže vám slúžiť: racemická zmes: Chiralita, príklady

Pokiaľ ide o objem atómov, celkový počet z nich je prítomný v jednotkovej bunke (1, 2, 3 atď.), ako aj jeho sférická geometria. Preto je vzorec trochu upravený:

Škaredý = (atómy č.) (Objem atómu)/ (objem jednotkovej bunky)

Ak chcete vypočítať škaredé, musíte určiť, potom č., V_atóm a v_Jednotka.

Jednoduchý kubický

Jednoduchá bunka kubickej jednotky. Zdroj: CCC_CRYSTAL_CELL_ (nepriehľadné).Svg: *cobique_centre_atomes_par_maille.SVG: CDANG (Original Idea a SVG vykonanie), Samuel Dupré (3D Odeeeling with SolidWorks) Drive Práca: Daniele Pugliesi (Talk) Odvodná práca: Daniele Pugliesi, CC BY-SA 3.0, cez Wikimedia Commons

Najjednoduchšia jednotná bunka zo všetkých je jednoduchá kubická. V ňom máme v každom rohoch niektoré časti atómov. Ak uvidíme, všimneme si, že dĺžka do Z tejto bunky sa rovná 2R, pretože bunka definuje atómy. Objem jednotkovej bunky sa teda rovná:

Vložka_Jednotka = do³ (Objem kocky)

= (2R)³

= 8R³

Medzitým sa objem atómu bude rovnať:

Vložka_atóm = (4/3) πr³ (Objem gule)

Každý z rohov je zdieľaný ďalšími 8 susednými jednotkovými bunkami. Preto máme v každom rohu frakciu 1/8 a máme 8 z nich, je nám jedno, 1 atóm na jednotku bunky (1/8 x 8 = 1).

Faktor balenie je:

Škaredý = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

To znamená, v jednoduchej kubickej bunke zaberajú atómy 52% celého objemu skla.

Kubický sústredený v tele

Stanovenie objemu buniek

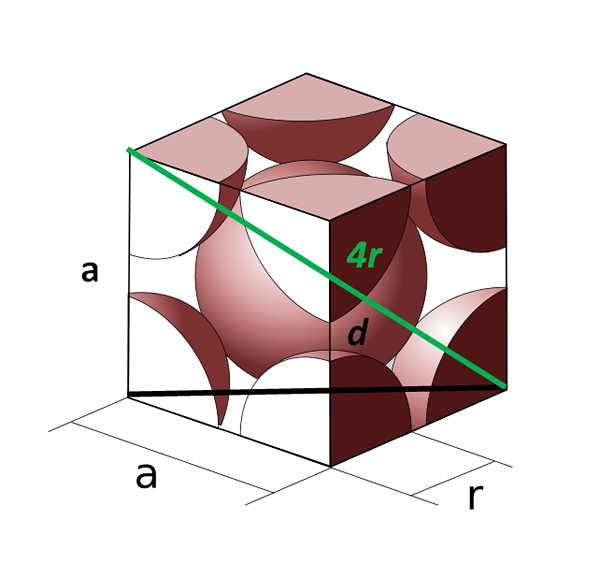Telesná jednotná bunka sústredená na tele. Zdroj: COBIQUE_CENTRE_ATOMES_PAR_MAILLE.SVG: CDANG (Original Idea a SVG vykonanie), Samuel Dupré (3D Odeeeling with SolidWorks) Derivátová práca: Daniele Pugliesi, CC BY-SA 3.0, cez Wikimedia Commons

Teraz sa pozrime na kubickú bunku sústredenú na tele. Strana do Už sa to nemôže rovnať 2R, pretože máme prázdny priestor medzi dvoma atómami rohov. Existuje preto diagonálna d rovná 4R (zelená farba), ktorá prechádza bunkou cez stred a dotýka sa opačných rohov a ďalšia diagonála d tváre (čierna).

Boky do, d a 4R nakreslite obdĺžnikový trojuholník, na ktorý môžeme na výpočet hodnoty aplikovať trigonometriu do:

(4R)² = d² + do²

Môže vám slúžiť: medzimolekulárne sily

Ale na druhej strane, v spodnej časti jednotkovej bunky máme ďalší trojuholník (do, do a d), na ktoré môžeme vypočítať hypotenus:

d²  = a² + do²

= 2a²

Výmena potom budeme mať:

(4R)² = (2²) + a²

(4R)² = 3a²

A = (4/√3) r

V_Jednotka rovná sa:

Vložka_Jednotka = a³

= ((4/√3) r)³

Stanovenie faktora balenia

Všimnite si, že s ohľadom na počet atómov máme vo vnútri tejto bunky 1 atóm, po rovnakom odpočítaní pre jednoduchú kubickú bunku a ďalší ďalší atóm, ktorý sa nachádza v strede bunky. Preto existuje celkom 2 atómy pre každú kubickú bunku zameranú na telo.

Balenie je potom:

Škaredý = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

To znamená, že v kubickej bunke zameranej na telo je 68% objemu skla obsadené atómami. V dôsledku toho je toto kryštalické usporiadanie kompaktnejšie (alebo hustejšie) ako jednoduché kubické.

Kubický sústredený na tvári

Stanovenie objemu buniek

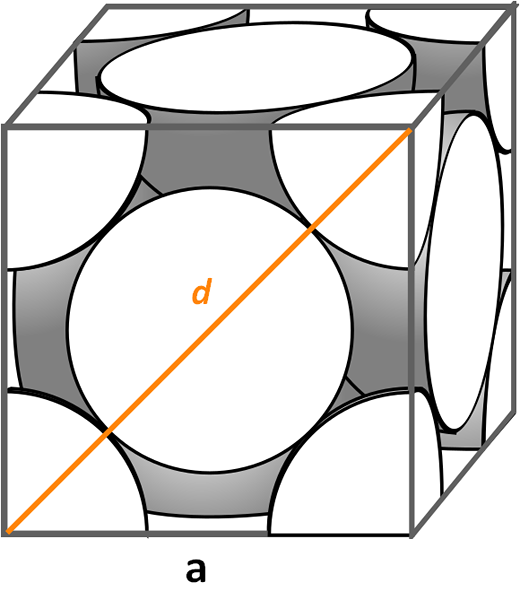Kubická jednotná bunka zameraná na tváre. Zdroj: CDang, CC BY-SA 3.0, cez Wikimedia Commons

Pozrime sa na kubickú jednotnú bunku zameranú na tváre, veľmi bežné v symfránoch anorganických solí a niektorých kovov, ako je zlato a striebro. Aby sme určili jeho balenie, musíme začať podľa predchádzajúcich príkladov, aby sme zistili, aký je objem jej jednotkovej bunky. Je potrebné znova vypočítať stranu do A tak objem kocky do³.

Tentoraz je postup ľahší a priamejší, pretože máme diagonálnu d Predná, spolu so stranami do, Tvoria pravý trojuholník, na ktorý môžeme aplikovať trigonometriu:

d² = a² + do²

= 2a²

Vyčistenie do budeme mať:

do = D/√2

Ale vizuálne si to všimneme d Je to rovná 4R, takže podráždíme substitúciu:

do = 4R/√2

= 2R 2^1-1/2

= (2√2) r

Byť v_Jednotka rovná:

do³ = ((2√2) r)³

= (16√2) r³

Pokiaľ ide o počet atómov na bunku, v každom rohu máme osem častí jedného atómu a tiež polovicu atómu pre každú zo šiestich tvárí, ktoré zdieľa iná susedná bunka. Preto sa počet atómov rovná:

Atómy č. = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Stanovenie faktora balenia

Mať to, že v každej kubickej bunke sú 4 atómy zamerané na tváre a tiež jej objem, ktorý sa rovná (16√2) r³, Potom môžeme vypočítať faktor balenia:

Škaredý = (atómy č.) (Objem atómu)/ (objem jednotkovej bunky)

= (4) (4/3) πr³ / (16√2) r³

Môže vám slúžiť: Acilo Group: Štruktúra, charakteristiky, zlúčeniny a deriváty

= π/(3√2) ≈ 74%

Všimnite si, že táto bunka je ešte kompaktnejšia ako predchádzajúce: 74% celkového objemu bunky je obsadené atómami. V dokonalom a čistom krištále by to bolo rovnocenné s tvrdením, že 26% jeho objemu je k dispozícii na hosťovanie ďalších atómov hostí.

Kompaktný hexagonálny

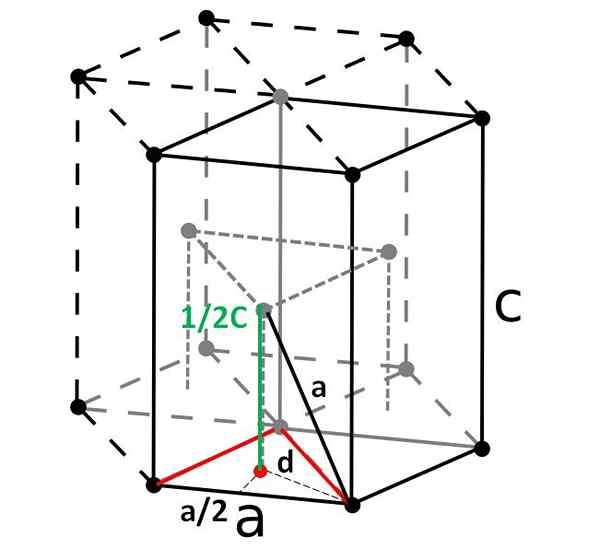Kompaktná šesťuholníková bunka a jej rhombohedrálna primitívna bunka. Zdroj: Originál: DornelfVector: DePiep, CC By-SA 3.0, cez Wikimedia Commons

Nakoniec, medzi najjednoduchším a najkompaktnejším jednotkovým bunkám máme kompaktný šesťuholník. Na rozdiel od predchádzajúcich je výpočet jeho objemu o niečo ťažší. Ako je vidieť, nie je kubický, takže má dva parametre do a c, Ten je výška bunky.

Stanovenie výšky bunky

Hexagonálna bunka sa dá rozdeliť na tri rhomboyanské bunky a od jedného z nich bude vypočítaná do a c. Strana do, Aj keď to nie je také zrejmé na obrázku vyššie, rovná sa 2R. Kalkulovať c, Namiesto toho používame trojuholník a produkt červeného bodu vnútorného trojuholníkového hranolu tej istej bunky.

Potrebujeme vypočítať vzdialenosť d Byť schopný určiť, koľko to stojí za to c. Na podlahe je červený trojuholník rovnostranný, s uhlom 60 °. Ale ak sa na stranách považuje za ďalší vnútorný obdĺžnikový trojuholník do/2 a d, a uhol 30 ° (polovica), potom pomocou trigonometrie môžeme určiť d:

Cos (30 °) = (do/2) / d

d = do/√3

A teraz uvažujeme o pravom trojuholníku zloženým zo strán c/2 (zelená), do (čierna) a d (bodkované):

do² = (do/√3)² + (C/2)²

Vyčistenie c Mali by sme:

c = √ (8/3) do

A výmena do Autor 2R:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2R)

= 4√ (2/3) r

Stanovenie objemu buniek

Ak chcete určiť objem šesťuholníkovej bunky. S vedomím, že rovnostranné trojuholníky majú strany do, Jeho výška sa vypočíta h. Nájdenie oblasti trojuholníka, ktorá je pre tento prípad √3/4do², Túto hodnotu vynásobíme 6, aby sme získali oblasť šesťuholníka: 3 (√3/2)do²

Zväzok je preto:

Vložka_Jednotka = Šesťhranná oblasť x výška

= 3 (√3/2)do² X 4√ (2/3) r

A znova nahradiť do Autor 2R:

Vložka_Jednotka  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Stanovenie faktora balenia

V šesťuholníkovej bunke je v rohoch 12 atómov, ktoré majú vo vnútri 1/6 ich zväzkov. Existujú tiež 3 vnútorné atómy, ktorých objemy sú kompletné, a ďalšie 2 atómy na horných a dolných tvárach, ktorých polovica jej objemov je vo vnútri bunky.

Preto sa počet atómov rovná:

Atóm č. = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atómov

A faktor balenia je konečne:

Škaredý = (atómy č.) (Objem atómu)/ (objem jednotkovej bunky)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Všimnite si, že faktor oddelenia pre šesťuholníkovú bunku je rovnaký ako pre kubickú bunku zameranú na tváre. To znamená, že obe sú rovnako kompaktné.

Odkazy

1. C. Barry Carter & M. Udeliť Norton. (2007). Veda a inžinierstvo keramických materiálov. Prubár.
2. Triasť a Atkins. (2008). Anorganická chémia. (Štvrté vydanie). MC Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Chémia. (8. vydanie.). Učenie sa.
4. Wikipedia. (2021). Atómový balenie. Zdroj: In.Wikipedia.orgán
5. Brandon. (2021). Čo je to faktor atómového balenia (a ako ho vypočítať pre SC, BCC, FCC a HCP)? Študent materiálov a inžinierstva. Obnovené z: msestudent.com