Normálne úsilie, z čoho pozostáva, ako sa vypočíta, príklady

On normálne úsilie Aplikuje sa na určitý materiál, ktorý sa tiež nazýva jednoosové úsilie, je to vzťah medzi aplikovanou silou kolmou na určitý povrch a krížovú oblasť, na ktorej pôsobí, alebo zaťaženie na jednotku plochy. Matematicky, ak p je veľkosť sily a A je oblasť, v ktorej sa používa, úsilie σ je kvocient: σ = p/a.

Jednotkami normálneho úsilia v medzinárodnom systéme sú Newton /Metro², Známy ako Pascal a skrátene PA. Toto sú rovnaké tlakové jednotky. Ostatné jednotky, ktoré sa objavujú v literatúre, sú často libry / palec² ani psi.

postava 1. Horniny sú neustále vystavené úsiliu v dôsledku tektonickej aktivity, čo spôsobuje deformácie v zemskej kôre. Zdroj: Pixabay.

Na obrázku 2 sa na krížovú oblasť aplikujú dve sily rovnakej veľkosť.

Tieto sily vyvíjajú normálne úsilie, ktoré sa tiež nazýva Axiálne zaťaženie stred, pretože jeho akcia sa zhoduje s axiálnou osou, na ktorej sa nachádza centroid.

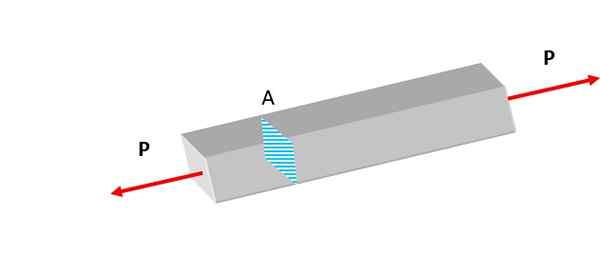Obrázok 2. Zobrazená lišta podlieha trakčným silám. Zdroj: Self Made.

Úsilie, či už normálne alebo iné typy, sa objavuje nepretržite v prírode. V litosfére sú horniny vystavené gravitácii a tektonickej aktivite, experimentujú deformácie.

Týmto spôsobom vznikajú štruktúry, ako sú záhyby a zlyhania, ktorých štúdium je dôležité pri používaní minerálov a stavebných inžinierstiev, pre výstavbu budov a ciest, aby sme vymenovali niekoľko príkladov.

[TOC]

Ako sa vypočítava?

Rovnica uvedená na začiatku σ = p/a umožňuje vypočítať priemerné normálne úsilie v príslušnej oblasti. Hodnota p je veľkosť výslednej sily nad oblasťou aplikovanou na ťažisko a je dostatočná pre mnoho jednoduchých situácií.

V tomto prípade je distribúcia síl jednotná, najmä v bodoch od miesta, kde máte bar predmetom trakcie alebo kompresie. Ale ak je úsilie potrebné na výpočet v konkrétnom bode alebo sily nie sú rovnomerne rozdelené, je potrebné použiť nasledujúcu definíciu:

Môže vám slúžiť: zatvorený elektrický obvod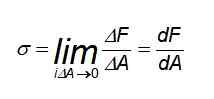

Potom sa vo všeobecnosti môže hodnota úsilia v konkrétnom bode líšiť od priemernej hodnoty. V skutočnosti sa úsilie môže líšiť v závislosti od časti, ktorú treba zvážiť.

Toto je znázornené na nasledujúcom obrázku, v ktorom sa trakčné sily F snažia oddeliť tyč v rovnováhe v častiach mm a nn.

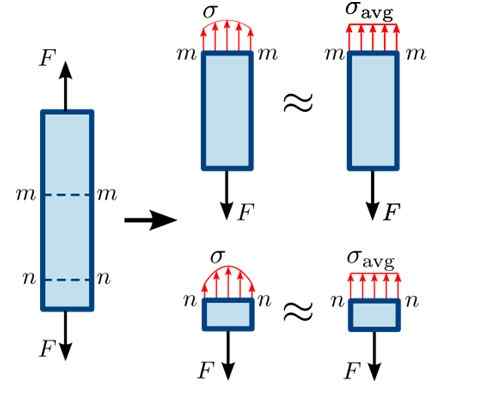Obrázok 3. Distribúcia normálneho úsilia v rôznych častiach baru. Zdroj: https: // commons.Wikimedia.org/wiki/file: normálne_stress.Svg#/médium/file: normálne_stress.SVG

Ako sekcia nn Je veľmi blízko k tomu, kde sily F dole, distribúcia síl na povrchu nie je úplne homogénna, títo maloletí sú ďalej od tohto bodu. Distribúcia je v sekcii o niečo homogénnejšia mm.

V každom prípade má normálne úsilie vždy tendenciu sa natiahnuť alebo stlačiť dve časti tela, ktoré sa nachádzajú na oboch stranách lietadla, na ktorej konajú. Na druhej strane, iné rôzne úsilie, ako napríklad šmyk, má tendenciu sa pohybovať a oddeliť tieto časti.

Hookeov zákon a normálne úsilie

Hookeov zákon uvádza, že v rámci elastických limitov je normálne úsilie priamo úmerné deformácii, ktorú zažíva bar alebo objekt. V tom prípade:

Normálne úsilie ∝ Unitárna deformácia

Contánska proporcionalita je mladým (Y) modulom:

Normálne úsilie (σ) = mladý modul (y) x jednotná deformácia (ε)

σ = y. ε

S ε = ΔL/l, kde AL je rozdiel medzi konečnou a počiatočnou dĺžkou, ktorá je l.

Mladý modul alebo modul elasticity je charakteristickým materiálom, ktorého rozmery sú rovnaké ako rozmery, pretože deformácia jednotky je bez rozmeru.

Môže vám slúžiť: 13 príkladov Newtonovho druhého zákona v každodennom živote

Dôležitosť úsilia voči odporu materiálov a geológie

Určenie, aké odolné sú materiály na úsilie, je veľmi dôležité. Pre štruktúry používané pri konštrukcii budov, ako aj pri návrhu častí pre rôzne zariadenia.

Materiály sa preto v laboratóriách dôkladne analyzujú prostredníctvom pokusov určených na to, aby vedeli, koľko sily môžu odolávať pred deformovaním a zlomením, čím stratia svoje funkcie. Na základe toho sa rozhoduje o tom, či vyrábať určitý kus alebo byť súčasťou zariadenia.

Predpokladá sa, že prvým vedcom, ktorý systematicky študoval odpor materiálov, bol Leonardo da Vinci. Zanechal dôkazy o pokusoch, v ktorých určil odpor vodičov visiacich kameňov rôznych pesos.

V úsilí je dôležitá veľkosť sily a tiež rozmery štruktúry a spôsob, akým sa uplatňuje, aby sa stanovili limity, v rámci ktorých má materiál elastické správanie; to znamená, že keď úsilie prestane, vracia sa k svojej pôvodnej podobe.

S výsledkami týchto testov sa krivky úsilia deformácie vykonávajú pre rôzne typy materiálov, ako sú oceľ, betón, hliník a mnoho ďalších.

Príklady

V nasledujúcich príkladoch sa predpokladá, že sily sú rozdelené rovnomerne a že materiál je homogénny a izotropný. To znamená, že jeho vlastnosti sú rovnaké v akomkoľvek smere. Preto je platné použiť rovnicu σ = p/a na nájdenie úsilia.

-Cvičenie 1

Na obrázku 3 je známe, že priemerné normálne úsilie pôsobiace na sekciu AB má veľkosť 48 kPa. Nájdite: a) veľkosť sily F, ktorá pôsobí v CB, b) úsilie v oddiele BC.

Môže vám slúžiť: Horizontálne snímanie: Charakteristiky, vzorce a rovnice, cvičenia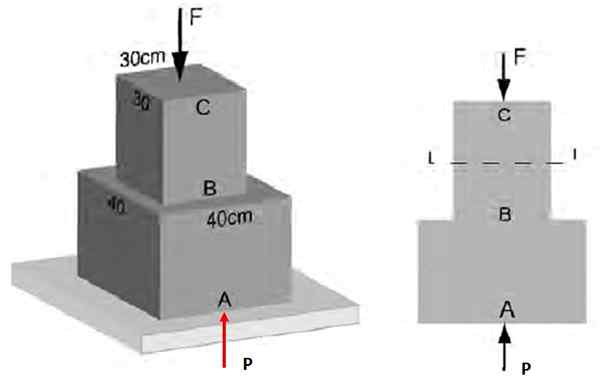Obrázok 4. Normálne úsilie na štruktúru príkladu 1 ..

Riešenie

Pretože štruktúra je v statickej rovnováhe, podľa Newtonovho druhého zákona:

P-f = 0

Normálne úsilie v časti AB má veľkosť:

σ_AB = P/a_AB

Kde p = σ_AB . Do_AB = 48000 PA. (40 x 10 ^-2 m)² = 7680 n

Preto f = 7680 n

Normálne úsilie v časti BC je pomer medzi veľkosťou F a plochou prierezu na tejto strane:

σ_Bc = F/a_Bc = 7680 N / (30 x 10 ^-2 m)² = 85.3 kPa.

-Cvičenie 2

150 m drôt dlhý a 2.5 mm s priemerom je natiahnutý silou 500 N. Nájsť:

a) Pozdĺžne úsilie σ.

b) jednotná deformácia, s vedomím, že konečná dĺžka je 150.125 m.

c) modul pružnosti A tento drôt.

Riešenie

a) σ = f / a = f / π.r²

Polomer drôtu je polovica priemeru:

R = 1.25 mm = 1.25 x 10^-3 m.

Oblasť prierezu je π.r², Potom je to úsilie:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 PA

b) ε = ΔL / l = (konečná dĺžka - počiatočná dĺžka) / počiatočná dĺžka

Preto:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Youngov modul drôtu sa vyčistí poznaním hodnôt ε a σ predtým vypočítaných:

Y = σ / ε = 101859.2 pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPa.

Odkazy

1. Pivo, f. 2010. Mechanika materiálov. 5. Vydanie. McGraw Hill. 7 - 9.
2. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^tónth  Edimatizovať. Sála. 238-242.
3. Hibbeler, R.C. 2006. Mechanika materiálov. 6. Vydanie. Pearson Vzdelanie. 22 -25
4. Valera Negrete, J. 2005. Všeobecné fyzikálne poznámky. Žobrák. 87-98.
5. Wikipedia. Stres (mechanika). Získané z: Wikipedia.orgán.