Termálna rovnovážna rovnice, aplikácie, cvičenia

Tepelná rovnováha dvoch telies, ktoré sú v tepelnom kontakte, je stav, ktorý sa dosahuje po dostatočne dlhom čase, aby sa teploty oboch tiel rovnali.

V termodynamike sa tepelný kontakt dvoch telies (alebo dvoch termodynamických systémov) chápe ako situácia, v ktorej majú telá mechanický kontakt alebo sú oddelené, ale v kontakte s povrchom, ktorý umožňuje iba tepelný priechod z jedného tela do druhého (diatermický povrch ).

postava 1. Po chvíli ľad a nápoj dosiahnu svoju tepelnú rovnováhu. Zdroj: Pixabay

Pri tepelnom kontakte by nemala existovať žiadna chemická reakcia medzi systémami v kontakte. Mala by existovať iba výmena tepla.

Každodenné situácie, v ktorých je výmena tepla, sú prezentované so systémami, ako je studený nápoj a sklo, horúca káva a čajová lyžička alebo telo a teplomer, medzi mnohými ďalšími príkladmi.

[TOC]

Keď sú dva alebo viac systémov v tepelnej rovnováhe?

Druhý termodynamický zákon ustanovuje, že teplo vždy prechádza z tela najvyššej teploty na najnižšiu teplotu. Prenos tepla prestane hneď po vyrovnávaní teplôt a dosiahnutí stavu tepelnej rovnováhy.

Praktická aplikácia tepelnej rovnováhy je teplomer. Teplomer je zariadenie, ktoré meria svoju vlastnú teplotu, ale vďaka tepelnej rovnováhe môžeme poznať teplotu iných tiel, napríklad teplotu osoby alebo zvieraťa.

Teplomer ortuťového stĺpca je umiestnený do tepelného kontaktu s telom, napríklad pod jazykom, a očakáva sa, že dostatok času dosiahne tepelnú rovnováhu medzi telom a teplomerom a že jeho čítanie sa nemení viac.

Keď sa tento bod dosiahne, teplota teplomeru je rovnaká ako telo.

Termodynamika s nulovým nulom uvádza, že ak je telo A v tepelnej rovnováhe s telom C a rovnaké telo C je v tepelnej rovnováhe s B, potom A a B sú v tepelnej rovnováhe, aj keď medzi A a B neexistuje žiadny termálny kontaktný kontakt.

Dospeli sme k záveru, že dva alebo viac systémov sú v tepelnej rovnováhe, keď majú rovnakú teplotu.

Tepelné rovnováhy

Predpokladáme telo pri počiatočnej teplote pri tepelnom kontakte s iným telom B s počiatočnou teplotou TBC. Tiež predpokladáme, že TA> TB, potom podľa druhého zákona sa teplo prenáša z A do B.

Po chvíli sa dosiahne tepelná rovnováha a obe telá budú mať rovnakú konečnú teplotu tf. To bude mať strednú hodnotu pre TA a TB, to znamená, ta> tf> tb.

Množstvo tepla prenášaného z A do B bude qa = ma ca (tf - ta), kde MA je hmotnosť tela A, Ca, tepelná kapacita na jednotku hmotnosti a y (tf - ta) teplotný rozdiel. Ak je TF menší ako potom QA je negatívny, čo naznačuje, že telo dáva teplo.

Podobne pre telo B musíte QB = MB CB (TF - TB); A ak je TF väčší ako TB, potom je QB pozitívny, čo naznačuje, že telo B prijíma teplo. Pretože telo A a B sú medzi nimi v tepelnom kontakte, ale izolované z prostredia, celkové množstvo vymeneného tepla by malo byť nulové: QA + QB = 0

Potom ma ca (tf - ta) + mb cb (tf - tb) = 0

Vyváženosť

Pri vývoji tejto expresie a vyčistení teploty TF sa získa konečná teplota tepelnej rovnováhy.

Obrázok 2. Teplota konečného zostatku. Zdroj: Self Made

Tf = (ma ca ta + mb cb tb) / (ma ca + mb cb).

V konkrétnom prípade zvážte prípad, že telá A a B sú identické pri hmotnosti a tepelnej kapacite, v tomto prípade bude rovnovážna teplota:

Tf = (ta + tb) / 2 ↔ Ak ma = mb a ca = cb.

Tepelný kontakt s fázovou zmenou

V niektorých situáciách sa stáva, že keď sú dve telá umiestnené do tepelného kontaktu, výmena tepla spôsobuje zmenu stavu alebo fázy v jednom z nich. Ak k tomu dôjde, treba sa vziať do úvahy, že počas fázovej zmeny nedochádza k zmene teploty v tele, ktorá modifikuje jeho stav.

Ak dôjde k fázovej zmene jedného z tela v tepelnom kontakte, použije sa koncept latentného tepla L, čo je energia na jednotku hmotnosti potrebnej na zmenu stavu:

Q = L ∙ M

Napríklad na topenie 1 kg ľadu pri 0 ° C, je potrebných 333,5 kJ/kg a táto hodnota je latentné teplo topenia ľadu.

Počas fúzie sa tuhá voda mení na kvapalnú vodu, ale táto voda si počas procesu fúzie udržiava rovnakú teplotu ľadu.

Žiadosti

Tepelná rovnováha je súčasťou každodenného života. Napríklad podrobne preskúmajme túto situáciu:

-Cvičenie 1

Osoba sa chce kúpať s teplou vodou pri 25 ° C. Na kocke umiestnite 3 litre studenej vody pri 15 ° C a v kuchyni zahrievajte vodu až do 95 ° C.

Koľko litrov horúcej vody musí pridať do kocky studenej vody, aby sa požadovala konečná teplota?

Riešenie

Predpokladajme, že je to studená voda a horúca voda:

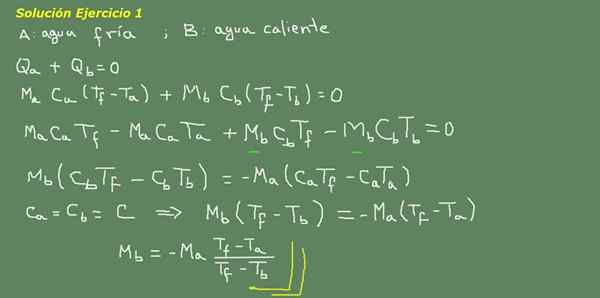Obrázok 3. Cvičenie 3 Riešenie. Zdroj: Self Made.

Navrhujeme tepelnú rovnovážnu rovnicu, ako je uvedené na doske na obrázku 3 a odtiaľ vyčistite vodu MB.

Počiatočná hmotnosť studenej vody je možné získať, pretože je známa hustota vody, ktorá je 1 kg pre každý liter. To znamená, že máme 3 kg studenej vody.

MA = 3 kg

Tak

MB = - 3 kg*(25 ° C - 15 ° C)/(25 ° C - 95 ° C) = 0,43 kg

Potom stačí s 0,43 LT horúcej vody, aby sa konečne získalo 3,43 litra teplej vody pri 25 ° C.

Vyriešené cvičenia

-Cvičenie 2

Zavádza sa kúsok kovu 150 g hmotnosti a teplota 95 ° C do nádoby obsahujúceho pol litra vody pri teplote 18 ° C. Po chvíli sa dosiahne tepelná rovnováha a teplota vody a kovu 25 ° C.

Predpokladajme, že nádoba s vodou a kusom kovu je uzavretý termos, ktorý neumožňuje výmenu tepla s prostredím.

Získajte špecifické kovové teplo.

Riešenie

Najprv vypočítame teplo absorbované vodou:

QA = MA CA (TF - TA)

QA = 500 g 1cal/(g ° C) (25 ° C - 18 ° C) = 3500 kalórií.

To je rovnaké teplo, ktoré dal kov:

QM = 150 g cm (25 ° C - 95 ° C) = -3500 kalórií.

Potom môžeme získať tepelnú kapacitu kovu:

Cm = 3500 Cal/ (150 g 70 ° C) = ⅓ Cal/ (g ° C).

Cvičenie 3

Máte 250 c.c. vody pri 30 ° C. K tejto vode, ktorá je v izolačnom termosku, sa pridá 25 g kocky ľadu pri 0 ° C s účelom jej ochladenia.

Určiť rovnovážnu teplotu; To znamená, že teplota, ktorá zostane, keď sa všetok ľad roztopí a ľadová voda sa zahrieva, až kým voda, ktorá pôvodne mala sklo.

Riešenie 3

Toto cvičenie je možné vyriešiť v troch etapách:

1. Prvým je fúzia ľadu, ktorá absorbuje teplo z počiatočnej vody, aby sa rozpustila a stala sa vodou.
2. Potom sa vypočíta teplo teploty v počiatočnej vode, pretože dala teplo (qCed<0) para fundir el hielo.
3. Nakoniec, roztavená voda (z ľadu) musí byť tepelne vyvážená vodou, ktorá spočiatku existovala.

Obrázok 4. Cvičenie 3 Riešenie. Zdroj: Self Made.

Vypočítajme teplo potrebné pre fúziu ľadu:

Qf = l * mh = 333,5 kJ/kg * 0,025 kg = 8 338 kJ

Potom teplo priradené vodou na rozpustenie ľadu je QCED = -QF

Toto teplo priradené vodou zostupuje jej teplote na hodnotu, ktorú môžeme vypočítať nasledovne:

T '= t0 - qf/(mA*Ca) = 22,02 ° C

Kde CA je tepelná kapacita vody: 4,18 kJ/(kg ° C).

Nakoniec pôvodná hmotnosť vody, ktorá je teraz pri 22,02 ° C, poskytne teplo na roztavenú vodu z ľadu, ktorý je pri 0 ° C.

Nakoniec sa rovnovážna teplota dosiahne po dostatočnom čase:

TE = (ma * t ' + mH * 0 ° C) / (ma + mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).

Nakoniec získanie rovnovážnej teploty:

TE = 20,02 ° C.

-Cvičenie 4

Olovo 0,5 kg opúšťa rúru pri teplote 150 ° C, čo je celkom pod jeho topením. Tento kus je umiestnený do nádoby s 3 litrami vody pri teplote miestnosti 20 ° C. Určite konečnú rovnovážnu teplotu.

Vypočítajte tiež:

- Množstvo tepla dodávané olovom do vody.

- Množstvo tepla absorbované vodou.

Údaje:

Špecifické olovo teplo: CP = 0,03 vápno/(g ° C); Špecifické vodné teplo: Ca = 1 vápno/(g ° C).

Riešenie 

V prvom rade určíme konečnú rovnovážnu teplotu TE:

TE = (ma ca ta + mp cp tp) / (MA CA + MP CP)

TE = 20,65 ° C

Potom množstvo tepla priradených olovom je:

QP = MP CP (TE - TP) = -1,94 x 10³ Lime.

Množstvo tepla absorbovaného vodou bude:

Qa = ma ca (te - ta) = +1,94x 10³ vápno.

Odkazy

1. Atkins, str. 1999. Fyzikálna chémia. Vydanie omega.
2. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
3. Giancoli, D. 2006. Fyzika: Princípy s aplikáciami. 6. ... Ed Prentice Hall.
4. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5. Edimatizovať. Pearson.
5. Resnick, r. (1999). Fyzický. Zvuk. 1. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.
6. Rex, a. 2011. Základy fyziky. Pearson.
7. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
8. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.