Nestabilná koncepcia a príklady rovnováhy

V mechanike je objekt v Nestabilná rovnováha Keď ho presuniete len zo svojej polohy silou, nevracia sa k nemu. Napríklad guľa z nasledujúceho obrázku, keď je nad pahorkou, je v nestabilnej rovnováhe, pretože najmenšie narušenie ju spôsobí hore nohami bez možnosti návratu vlastnými prostriedkami.

postava 1. Lopta je v nestabilnej rovnováhe v polohe vľavo, v ľahostajnej rovnováhe v strede a v stabilnej rovnováhe vpravo. Zdroj: Wikimedia Commons.

Na druhej strane, keď je lopta na rovnom povrchu, rovnako ako v polohe stredu, hovorí sa, že je v ľahostajnosť alebo neutrálny. Sila, ktorá ju narúša, sa dá aplikovať, presunúť ju na inú stranu, ale ak sila zmizne, lopta bude opäť stabilná.

Nakoniec, vpravo, lopta je na spodku konkávnej misy. Táto pozícia je tiež vyvážená, ale stabilná rovnováha. Sila, ktorá narúša loptu, sa dostane len k oscilácii okolo pôvodnej polohy, aby sa k nej vrátila.

[TOC]

Príčiny straty zostatku

Bežné predmety (a ľudia a zvieratá) strácajú rovnováhu a pád z dôvodu krútiaceho momentu vzniku hmotnosti, sila vyvíjaná Zemou na všetky predmety blízko jej povrchu. Keď máte predĺžené telo, bod, v ktorom sa váha volá gravitačný centrum.

Hmotnosť môže byť vyvážená vďaka podpore, ako je ten, ktorý poskytuje povrch, a týmto spôsobom sa objekt nepohybuje. Ale stále má možnosť obrátiť sa v súvislosti s určitým bodom, pretože v rozšírených objektoch nie je rovnováha síl jediným faktorom, ktorý ich udržuje v pokoji, ale aj miestom, kde sa tieto sily aplikujú.

Nižšie je obrázok s vyváženou ceruzkou na špičke, v nestabilnej rovnováhe. Akýkoľvek vzduchový prúd to ukáže, ale medzitým sa kompenzuje normálna hmotnosť a sila, ktorá sa sami podporuje. Okrem toho majú obe sily rovnakú činnosť konania a to prechádza špičkou ceruzky, čo zaisťuje rovnováhu.

Môže vám slúžiť: Non -coplanárne vektory: Definícia, podmienky, cvičenia

Ale ak sa ceruzka trochu nakloní, ako je uvedené vpravo, línia pôsobenia hmotnosti prechádza cez špičku, ktorá pôsobí ako čap. Potom hmotnosť vytvára neolákavý krútiaci moment a ceruzka sa točí v smere rúk hodín.

Obrázok 2. Ceruzka podopretá na jej špičke je v nestabilnej rovnováhe, malé narušenie spôsobí, že hmotnosť spôsobí krútiaci moment vzhľadom na špičku a ceruzka klesne. Zdroj: f. Zapata.

Faktory, ktoré zaručujú stabilitu

Takmer vždy to, čo sa požaduje, je stabilná rovnováha, pretože nestabilná rovnováha je, ako naznačuje jej názov, dosť neistý. Pokračovanie v príklade ceruzky, akonáhle padne a zostáva vodorovne na povrchu, nová poloha je oveľa stabilnejšia ako keď sa zastavila na špičke.

Dôvodom je, že na jednej strane je ťažisko bližšie k povrchu a na druhej strane je podporný povrch ceruzky oveľa väčší.

Keď je podporná plocha lar. A ak je vzdialenosť od stredu gravitácie k povrchu nižšia, rameno páky hmotnosti je nižšie, a preto je krútiaci moment tiež.

Záverom je, že čím väčší je základ podpory objektu a bližší jeho ťažisko k podlahe, tým menšia je pravdepodobnosť prevrátenia a rovnováha má tendenciu byť stabilná. Bábätká to vedia, a preto zvyčajne praskajú najskôr skôr, ako riskujú stáť.

A ak namiesto toho, aby bolo podporované, je telo pozastavené z bodu, umiestnenie ťažiska má tiež významnú úlohu pri stanovovaní rovnováhy, ako bude vidieť krátko v nasledujúcich príkladoch.

Môže vám slúžiť: Mount Olympus (Mars)

Príklady rovnováhy

Rovnováha v podporovaných telách

Zostatok v podporovaných telách závisí, ako je uvedené, na:

-Ako blízko stredu gravitácie povrchu.

-Veľkosť základne objektu.

Zvážte kužeľ na plochom stole. Najstabilnejšou polohou je bezpochyby, keď je základňa kužeľa plne podopretá na stole. Toto je stabilná rovnovážna poloha, pretože ťažisko kužeľa je na osi symetrie a bližšie k jej základni ako k špičke.

Ľahostajná rovnováha sa dosiahne umiestnením kužeľa a nestabilná rovnováha zodpovedá kužele na jeho špičke, ako je ceruzka, ktorá nemusí byť ľahká úloha, vzhľadom na to, že najmenší pohyb sa kužeľ otočí.

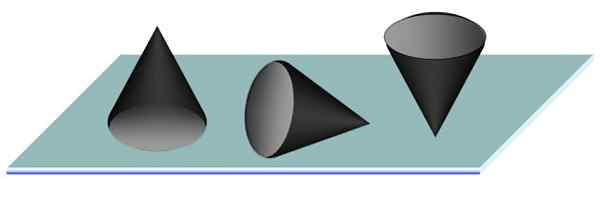Obrázok 3. Stabilná, ľahostajná a nestabilná rovnováha kužeľa podporovaného na stole. Zdroj: f. Zapata.

Rovnováha v pozastavených orgánoch

Je bežné nájsť pozastavené telá, ktoré visia aspoň jeden bod, napríklad obrazy a lampy. Pri stanovení rovnováhy je potrebné zvážiť umiestnenie ťažiska a umiestnenie vpredu.

Situácia sa dá ľahko vizualizovať pomocou obdĺžnika. Tu sa ťažisko zhoduje s geometrickým centrom obrázku, ktoré za predpokladu, že hmotnosť objektu je distribuovaná rovnomerne.

Na umiestnenie plachty do nestabilnej rovnováhy je zavesený z bodu, ktorý sa nachádza pod Z ťažiska, dokonca len drží plachtu medzi prstami bez toho, aby sa príliš utiahla, aby mu zanechala slobodu pohybu.

Malá sila je dostatočná na to, aby sa placht okamžite otočil v jednom alebo druhom zmysle. Dôvodom je rovnaký ako v prípade podporovaného objektu: Hmotnosť vyvíja nekompromisný krútiaci moment, ktorý uľahčuje rotáciu tela.

Môže vám slúžiť: Riešenie teplo: Ako sa vypočítava, aplikácie a cvičenia

Pri otáčaní plachta prechádza polohou, ktorá je stabilnej rovnováhy, v ktorej zostáva bod suspenzie zhora strediska gravitácie. Okolo tejto polohy sa trochu pohybuje a nakoniec sa zastaví.

Ak sa znova aplikuje sila, lamina sa opäť pohybuje, ale opäť sa vráti do tejto polohy, v ktorej sú bod odpruženia a stred gravitácie zarovnané s vertikálnou.

Nakoniec sa indiferentná rovnováha kontroluje prejdením kolíka presne cez stred gravitácie. Ak je hárok otočený, aby zostal na rôznych pozíciách, je zrejmé, že medzi nimi nebude väčší rozdiel.

Záverom možno povedať, že pre telá zavesené v nestabilnej rovnováhe je bod suspenzie pod ťažiskom. A opak pre stabilnú rovnováhu.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
3. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5. Edimatizovať. Pearson.
4. Resnick, r. (1999). Fyzický. Zvuk. 1. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka.
5. Rex, a. 2011. Základy fyziky. Pearson.
6. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.