Fyzický

Charakteristiky a príklady elipsoidu

Charakteristiky a príklady elipsoidu

On elipsoid Je to povrch v priestore, ktorý patrí skupine kvadrických povrchov a ktorej všeobecná rovnica je formy:

Sekera2 + Podľa2 + Cz2 + DXY + EXZ + FYZ + GX + HY + IZ + J = 0

Je to trojrozmerný ekvivalent elipsy, ktorý sa vyznačuje eliptickými a kruhovými stopami v niektorých osobitných prípadoch. Stopy sú krivky, ktoré sa získavajú pri pretínaní elipsoidu s rovinou.

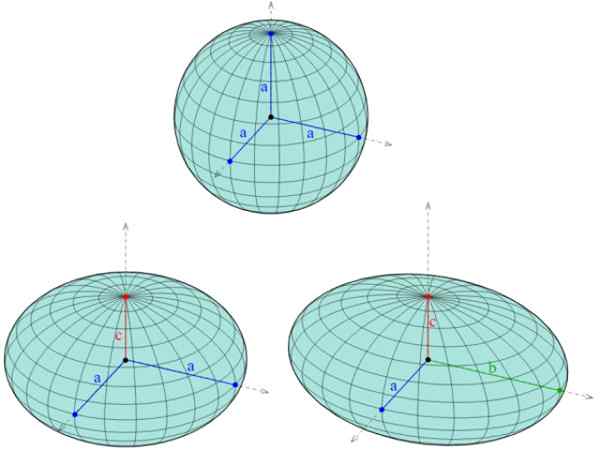
postava 1. Tri rôzne elipsoidy: nad guľou, v ktorej sú tri polovičné semeis rovnaké, dole doľava sféroid, s dvoma rovnakými polovicou a -on -a -nou semi -osou a nakoniec doprava, triaxiálny sféroid, s tromi osami inú dĺžku. Zdroj: Wikimedia Commons. AG2GAEH/CC BY-S (https: // creativeCommons.Org/licencie/By-SA/4.0)

Okrem elipsoidu existuje päť ďalších kvadriiek: hyperboloid jedného listu a dva listy, dva typy paraboloidov (hyperbolické a eliptické) a eliptický kužeľ. Jeho stopy sú tiež kónické.

Elipsoid môže byť tiež vyjadrený štandardnou rovnicou v karteziánskych súradniciach. Ellipsoid zameraný na pôvod (0,0,0) a vyjadrený týmto spôsobom pripomína elipsu, ale s ďalším pojmom:

Hodnoty do, b a c Sú to skutočné čísla väčšie ako 0 a predstavujú tri elipsoidné polovica.

[TOC]

Vlastnosti elipsoidu

- Štandardná rovnica 

Štandardná rovnica v karteziánskych súradniciach pre elipsu zameraná na bod (H, k, m) je:

- Parametrické rovnice elipsoidu

V sférických súradniciach možno elipsoid opísať takto:

x = hriech 9. cos φ

y = b hriech θ. hriech φ

Z = c cos θ

Elipsoidové semi -out sú stále A, B a C, zatiaľ čo parametre sú uhly 9 a φ z nasledujúceho obrázku:

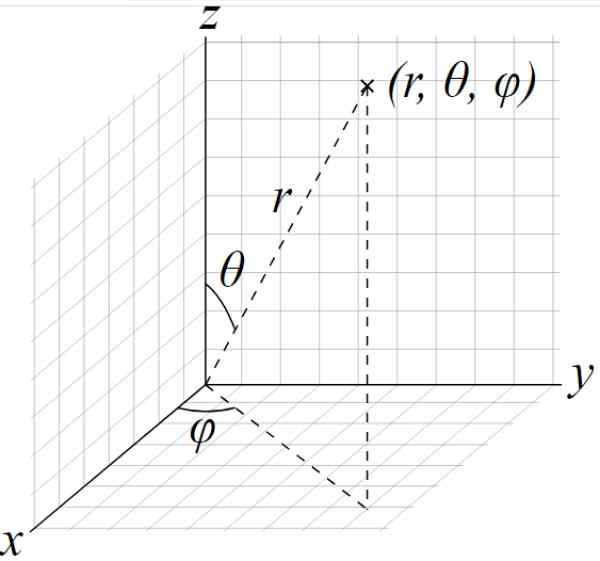Obrázok 2. Sférický súradnicový systém. Elipsoid sa môže parametrizovať pomocou uhlov zobrazených theta a phi ako parametre. Zdroj: Wikimedia Commons. Doména Anggs / Pub.

- Elipsoidové stopy

Všeobecná rovnica povrchu vo vesmíre je f (x, y, z) = 0 a stopy povrchu sú krivky:

Môže vám slúžiť: Vektorová veľkosť

- x = c; F (c, y, z) = 0

- y = c; F (x, c, z) = 0

- Z = c; F (x, y, c) = 0

V prípade elipsoidu sú také krivky elips a niekedy obvody.

- Zväzok

Objem V elipsoidu je daný (4/3) π -násobkom produktu jeho troch polovíc:

V = (4/3) π. ABC

Špeciálne elipsoidné prípady

-Ellipsoid sa stáva guľou, keď sú všetky polovičné veľkosť rovnakej veľkosti: a = b = c ≠ 0. To dáva zmysel, pretože elipsoid je ako guľa, ku ktorej sa v každej osi roztiahla inak.

-Sféroid je elipsoid, v ktorom sú dvaja polojes identickí a tretí je iný, napríklad by to mohol byť a = b ≠ c.

Sféroid sa tiež nazýva revolúcia elipsoid, pretože sa dá generovať otočením elips okolo osi.

Ak sa otočná os zhoduje s hlavnou osou, sféroid je množenie, Ale ak sa zhoduje s menšou osou, je to zatlačiť:

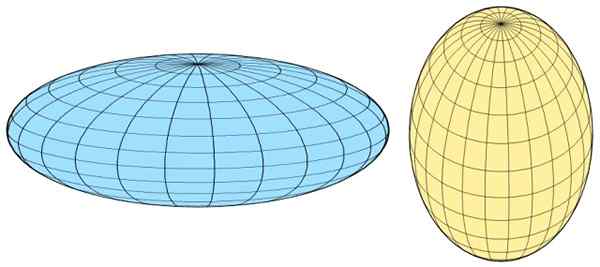Obrázok 3. Sféroid doľava doľava a sféroidná prolitácia doprava. Zdroj: Wikimedia Commons.

Miera sploštenia sféroidu (elipticita) je daná rozdielom v dĺžke medzi dvoma semipágmi, vyjadrenými vo frakčnej forme, to znamená, že je to jednotka sploštenie, daná:

F = (a - b) / a

V tejto rovnici A predstavuje semi -senije a b menšiu osi, nezabudnite, že tretia os sa rovná ktorejkoľvek z nich pre sféroid. Hodnota F je medzi 0 a 1 a pre sféroid musí byť väčšia ako 0 (ak by sa rovná 0, jednoducho by sme mali guľu).

Môže vám slúžiť: Bethelgeuse

Referenčný elipsoid

Planéty a všeobecne hviezdy nie sú zvyčajne dokonalé sféry, pretože pohyb rotácie okolo ich sekerov, ktorý sa vyrovná tela v póloch a bassinoch v Ekvádore.

Z tohto dôvodu sa zdá, že Zem je ako obláčna sféroidná, aj keď nie tak prehnaná ako u predchádzajúcej postavy, a na druhej strane je plynný Saturn Giant najtvrdší z planét v slnečnej sústave.

Realistickejší spôsob reprezentácie planét je teda predpokladať, že sú ako sféroid alebo elipsoid revolúcie, ktorého semi -seme -major je rovníkové rádio a menšie semi -osi polárny polomer.

Starostlivé opatrenia prijaté na svete umožnili vybudovať Referenčný elipsoid Zeme ako jej najpresnejšej formy na matematickú prácu.

Hviezdy majú tiež pohyby rotácie, ktoré im dávajú viac alebo menej sploštené formy. Hviezda rýchleho Aternara, ôsma najjasnejšia hviezda na nočnej oblohe, v južnej konštelácii Eridanusu je pozoruhodne eliptická, keď ju porovnáva s väčšinou. Je to 144 svetelných rokov od nás.

Na druhej strane, pred niekoľkými rokmi, vedci dali s doteraz sférickejším objektom: Kepler 11145123 hviezda, 5 000 svetelných rokov, s veľkosťou nášho slnka a rozdielom medzi semifinágmami iba 3 km. Ako sa očakávalo, tiež sa otáča pomalšie.

Pokiaľ ide o Zem, nie je to dokonalý sféroid kvôli jeho robustnému povrchu a miestnym variáciám gravitácie. Z tohto dôvodu je zvolená viac ako jedna dostupná referenčná sféroid.

Môže vám slúžiť: Čo je údolie vo fyzike? (S príkladmi)

Pomoc satelitov je neoceniteľná pri vytváraní stále presnejších modelov tvaru Zeme, a to je známe napríklad, že južný pól je bližšie k Ekvádoru ako severný pól ako severný pól.

Obrázok 4. Haumea, transneptunská trpaslík planéta má elipsoidálny tvar. Zdroj: Wikimedia Commons.

Numerický príklad

V dôsledku rotácie Zeme sa generuje odstredivá sila, ktorá jej dáva podobu podlhovastého elipsoidu namiesto gule namiesto gule. Je známe, že rovníkové rádio Zeme je 3963 míľ a polárny polomer je 3942 míľ.

Nájdite rovnicu rovníkovej stopy, rovnice tohto elipsoidu a mieru jej sploštenia. Porovnať tiež s Ellipticity Saturn, s údajmi uvedenými nižšie:

-Saturn Rovníkové rádio: 60268 km

-Saturn Polar Radio: 54364 km

Riešenie

Vyžaduje sa súradnicový systém, ktorý predpokladáme zameraný na pôvod (stred zeme). Budeme predpokladať vertikálnu os z a stopy, ktorá zodpovedá rovníkovi, je na rovine xy, čo je ekvivalentné rovine z = 0.

V rovníkovej rovine sú semi -a a b rovnaké, preto a = b = 3963 míľ, zatiaľ čo c = 3942 míľ. Toto je špeciálny prípad: sféroid zameraný na bod (0,0,0), ako je uvedené vyššie.

Rovníková stopa je kruh polomeru R = 3963 míľ, zameraný na pôvod. Vypočíta sa vykonaním z = 0 v štandardnej rovnici:


A štandardná rovnica zemského elipsoidu je:

Nakoniec sa vypočíta opatrenie nastavenia (eliptické) hodnotenie v rovnici:

F Pôda = (a - b) / a = (3963-3942) míle / 3963 míľ = 0.0053

F Saturn = (60268-54363) km/60268 km = 0.0980

Všimnite si, že eliptický F je bezrozmerné množstvo.

Odkazy

  1. Arcgis pre pracovnú plochu. Sféroidné a sféry. Obnovené z: Desktop.Oblúk.com.
  2. Svet BBC. Tajomstvo najférickejšieho objektu, aké kedy bolo objavené vo vesmíre. Zdroj: BBC.com.
  3. Larson, R. Výpočet a geometria. Šieste vydanie. Zväzok 2. McGraw Hill.
  4. Wikipedia. Elipsooid. Zdroj: In.Wikipedia.orgán.
  5. Wikipedia. Siperoid. Zdroj: In.Wikipedia.orgán.