Polynomické rovnice

Čo sú to polynómové rovnice?

Ten Polynomické rovnice Sú vyhlásením, ktoré zvyšuje rovnosť dvoch výrazov alebo členov, kde aspoň jeden z termínov, ktoré tvoria každú stranu rovnosti, sú polynómy P (x). Tieto rovnice sú pomenované podľa stupňa ich premenných.

Všeobecne platí, že rovnica je vyhlásenie, ktoré stanovuje rovnosť dvoch výrazov, kde aspoň v jednom z nich existujú neznáme sumy, ktoré sa nazývajú premenné alebo neznámy. Aj keď existuje veľa typov rovníc, sú všeobecne klasifikované do dvoch typov: algebraické a transcendentné.

Polynomické rovnice obsahujú iba algebraické výrazy, ktoré môžu mať jeden alebo viac neznámych, ktoré zasahujú do rovnice. Podľa exponentu (známka), ktorú majú, môžu byť klasifikované ako: prvé triedu (lineárne), druhý stupeň (kvadratický), tretí stupeň (kubický), štvrtý stupeň (quantic), stupňa väčšie alebo rovné päť a iracionálny.

Charakteristiky polynómových rovníc

Polynomické rovnice sú výrazy, ktoré sú tvorené rovnosťou medzi dvoma polynómami; To znamená, pre konečné sumy multiplikácií medzi hodnotami, ktoré nie sú známe (premenné) a pevné čísla (koeficienty), kde premenné môžu mať exponenty a ich hodnota môže byť kladné celé číslo, vrátane nuly.

Exponenti určujú stupeň alebo typ rovnice. Tento termín výrazu, ktorý má exponent najhodnotnejšej hodnoty, bude predstavovať absolútny stupeň polynómu.

Polynomické rovnice sú známe aj ako algebraické, ich koeficienty môžu byť skutočnými alebo zložitými číslami a premenné sú neznáme čísla reprezentované písmenom, napríklad: „x“.

Ak nahradením hodnoty za premennú „x“ v p (x) sa výsledok rovná nule (0), potom sa hovorí, že táto hodnota spĺňa rovnicu (ide o riešenie) a všeobecne sa nazýva polynomiálny koreň.

Keď je vyvinutá polynómová rovnica, všetky korene alebo riešenia sa chcú nájsť.

Typy polynómových rovníc

Existuje niekoľko typov polynómových rovníc, ktoré sú diferencované podľa počtu premenných, a tiež podľa ich stupňa ich exponentov.

Polynomické rovnice -kde jeho prvé funkčné obdobie je polynóm, ktorý má iba jeden neznámy, vzhľadom na to, že jeho stupeň môže byť akékoľvek prirodzené číslo (n) a druhý termín je nulová -môže byť vyjadrená nasledovne:

Môže vám slúžiť: História trigonometrie z jej pôvodu

do_{N *} Xⁿ + do_{N-1 *} X^N-1 +… + A_{1 *} X¹ + do_{0 *} X₀ = 0

Kde:

• do_n, do_N-1 už₀, Sú to skutočné koeficienty (čísla).
• do_n sa líši od nuly.
• Exponent n je pozitívne celé číslo, ktoré predstavuje stupeň rovnice.
• x je premenná alebo neznáma, ktorá sa musí hľadať.

Absolútny alebo vyšší stupeň polynómovej rovnice je ten, že exponent väčšej hodnoty medzi všetkými tými, ktorí tvoria polynóm; Týmto spôsobom sú rovnice klasifikované ako:

Prvá trieda

Polynomické rovnice prvého stupňa, známe tiež ako lineárne rovnice, sú tie, ktoré sa stupň (najväčší exponent) rovná 1, polynóm je vo forme p (x) = 0; A je zložený z lineárneho a nezávislého pojmu. Je to napísané takto:

AX + B = 0.

Kde:

• A a B sú skutočné čísla a ≠ 0.
• Sekera je lineárny termín.
• B je nezávislý termín.

Napríklad rovnica 13x - 18 = 4x.

Na vyriešenie lineárnych rovníc sa musia všetky výrazy obsahovať neznáme X odovzdať na stranu rovnosti a tie, ktoré sa nemajú pohybovať na druhej strane, aby sa vyčistili a získali riešenie:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Týmto spôsobom má daná rovnica iba jedno riešenie alebo koreň, čo je x = 2.

Druhý stupeň

Polynomické rovnice druhého stupňa, známe tiež ako kvadratické rovnice, sú tie, v ktorých sa stupeň (najväčší exponent) rovná 2, polynóm je formy p (x) = 0 a je zložený z kvadratického pojmu, a lineárne a nezávislé. Vyjadruje sa takto:

sekera² + BX + C = 0.

Kde:

• A, B a C sú skutočné čísla a ≠ 0.
• sekera² Je to kvadratický termín a „A“ je koeficient kvadratického pojmu.
• BX je lineárny termín a „B“ je koeficient lineárneho pojmu.
• C je nezávislý termín.

Rozlíšenie

Všeobecne platí, že riešenie tohto typu rovníc je uvedené pri zúčtovaní X rovnice a zostáva nasledovne, čo sa nazýva rozlíšenie:

Môže vám slúžiť: binomická veta

Tam, (b² - 4ac) sa nazýva diskriminácia z rovnice a tento výraz určuje počet riešení, ktoré môže mať rovnica:

• Áno b² - 4ac) = 0, rovnica bude mať jedno riešenie, ktoré je dvojité; to znamená, že bude mať dve rovnaké riešenia.
• Áno b² - 4ac)> 0, rovnica bude mať dve rôzne skutočné riešenia.
• Áno b² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Napríklad máte 4x rovnicu² + 10x - 6 = 0, na jeho vyriešenie najskôr sú identifikované pojmy A, B a C a potom sa nahradia vo vzorci:

A = 4

B = 10

C = -6.

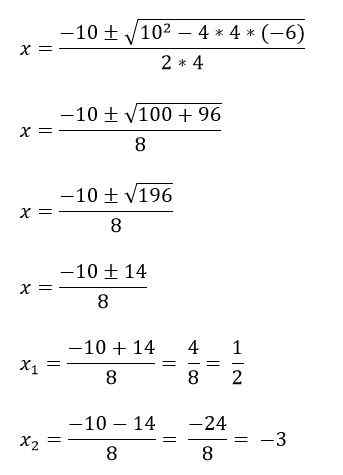
Existujú prípady, v ktorých druhé polynómové rovnice nemajú tri výrazy, a preto sa vyriešia inak:

• V prípade, že kvadratické rovnice nemajú lineárny termín (tj b = 0), rovnica bude vyjadrená ako AX² + C = 0. Na jeho vyriešenie, X sa vyčistí² A odmocninové korene sa uplatňujú u každého člena a nezabudnite, že dva možné príznaky, ktoré môžu mať neznáme, môžu mať:

sekera² + C = 0.

X² = - C ÷ a

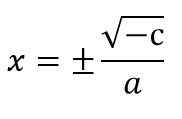
Napríklad 5 x² - 20 = 0.

5 x² = 20

X² = 20 ÷ 5

x = ± √4

x = ± 2

X₁ = 2.

X₂ = -2.

• Ak kvadratická rovnica nemá nezávislý termín (tj C = 0), rovnica bude vyjadrená ako AX² + Bx = 0. Na jeho vyriešenie sa musí spoločný faktor neznámeho X uberať u prvého člena; Keďže sa rovnica zhoduje s nulou, je splnené, že aspoň jeden z faktorov sa bude rovnať 0:

sekera² + Bx = 0.

x (ax + b) = 0.

Týmto spôsobom musíte:

x = 0.

x = -b ÷ a.

Napríklad: máte rovnicu 5x² + 30x = 0. Najprv je to faktor:

5x² + 30x = 0

x (5x + 30) = 0.

Generujú sa dva faktory, ktoré sú x y (5x + 30). Jeden z nich sa bude považovať za nulu a druhý je daný riešenie:

X₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

X₂ = -6.

Najvyšší stupeň

Hlavné polynómové rovnice sú tie, ktoré sa pohybujú od tretieho stupňa, ktoré je možné vyjadriť alebo rozlíšiť všeobecnou polynómovou rovnicou pre akýkoľvek stupeň:

Môže vám slúžiť: korelačný koeficient: vzorce, výpočet, interpretácia, príklad

do_{N *} Xⁿ + do_{N-1 *} X^N-1 +… + A_{1 *} X¹ + do_{0 *} X₀ = 0

Používa sa, pretože rovnica s stupňom vyšším ako dva je výsledkom faktorizácie polynómu; to znamená, že sa vyjadruje ako znásobenie prvého alebo väčšieho polynómu, ale bez skutočných koreňov.

Riešenie tohto typu rovníc je priame, pretože násobenie dvoch faktorov sa bude rovnať nule, ak je niektorý z faktorov nulová (0); Preto musí byť každá z nájdených polynómových rovníc vyriešená, čím sa každý z jeho faktorov zhoduje s nulou.

Napríklad máte rovnicu tretieho stupňa (kubické) x³ + X² +4x + 4 = 0. Ak chcete vyriešiť, musíte postupovať podľa nasledujúcich krokov:

• Podmienky sú zoskupené:

X³ + X² +4x + 4 = 0

(X³ + X² ) + (4x + 4) = 0.

• Členovia sa rozpadnú, aby získali spoločný faktor neznámeho:

X² (x + 1) + 4 (x + 1) = 0

(X² + 4)_*(x + 1) = 0.

• Týmto spôsobom sa získajú dva faktory, ktoré sa musia rovnať nule:

(X² + 4) = 0

(x + 1) = 0.

• Je zrejmé, že faktor (x² + 4) = 0 nebude mať skutočné riešenie, zatiaľ čo faktor (x + 1) = 0 Áno. Preto riešenie je:

(x + 1) = 0

x = -1.

Vyriešené cvičenia

Vyriešiť nasledujúce rovnice:

Prvé cvičenie

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Riešenie

V tomto prípade je rovnica vyjadrená ako násobenie polynómov; to znamená, že je faktorizovaný. Na jeho vyriešenie sa musí každý faktor rovnať nule:

2x² + 5 = 0, nemá žiadne riešenie.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

Týmto spôsobom má daná rovnica dve riešenia: x = 3 a x = -1.

Druhé cvičenie

X⁴ - 36 = 0.

Riešenie

Dal sa polynóm, ktorý je možné opísať ako rozdiel v štvorci, aby sa dosiahol rýchlejšie roztok. Rovnica teda zostáva:

(X² + 6)_*(X² - 6) = 0.

Na nájdenie riešenia rovníc sa oba faktory rovnajú nule:

(X² + 6) = 0, nemá žiadne riešenie.

(X² - 6) = 0

X² = 6

x = ± √6.

Počiatočná rovnica má teda dve riešenia:

x = √6.

x = - √6.