Arrheniusova rovnica
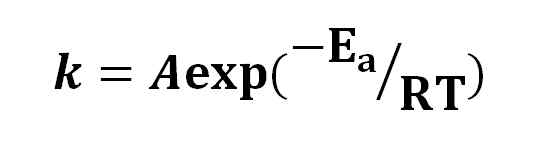
- 4665
- 37
- Blažej Hrmo
Aká je Arrheniusova rovnica?
Ten Arrheniusova rovnica Je to prístup, ktorý súvisí s rýchlosťou konštanty chemickej reakcie v závislosti od teploty. Založil ho v roku 1899 švédsky chemik Svante Arrhenius (1859-1927). Predstavuje jeden z najzákladnejších príspevkov pri vývoji chemickej kinetiky.
Táto rovnica vďačí za svoje teoretické základne mnohým vedcom, vrátane Wihelmy (1850), Berthelot (1862) a J. J. Hood (1885). Najväčší vplyv sa však pripisuje vytvoreniu Arrheniusovej rovnice s prácou vykonanou van't Hoofom (1884), ktorý vytvoril závislosť od rovnovážnych konštantov chemických reakcií s teplotou.
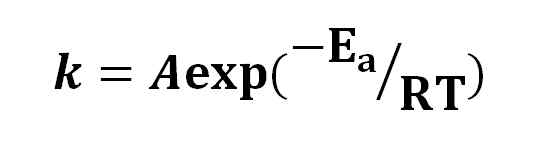 Arrheniusova rovnica. Zdroj: Gabriel Bolívar.
Arrheniusova rovnica. Zdroj: Gabriel Bolívar. Na základe rovnice Arrhenius, myšlienka, že zvýšenie o 10 ° C spôsobilo duplikáciu reakčnej rýchlosti. Ďalšie interpretácie, ktoré sa stávajú, je to, že molekuly potrebujú určitú aktivačnú energiu, aby sa navzájom reagovali.
Podobne sa zdôrazňuje, že Arrheniusova rovnica je ďalšou formou exponenciálneho rozpadu, v ktorej hodnota rýchlosti konštanty v závislosti od exponentu -edo/Rt, kde edo je aktivačná energia.
Rovnica a vysvetlenie
Arrheniusova rovnica má tieto dva výrazy tieto dva výrazy:
K = ae-EA/RT
Forma rovnice použitej v chémii a súvisí s mólmi činidiel.
K = ae-EA/KBT
Forma rovnice používanej vo fyzike a súvisí s viac molekulami, ako s krtkami.
Obidve odvodzujú z Van´s Hoofova rovnica pre variáciu rovnovážnej konštanty K v závislosti od teploty. Základná rovnica je:
d (ln k)/dt = edo/Rt2
Môže vám slúžiť: dibenzalacetona: vlastnosti, reakčný mechanizmus, použitie, rizikáČo je integrované za predpokladudo je nezávislý od teploty. Takže máme:
ln k = - edo/Rt + ln a
Kde ln a je integračná konštanta. Ak sa exponenciálna funkcia aplikuje na oboch stranách rovnice, získame už zavedenú rovnicu Arrhenius.
Komponenty
klimatizovať
Je to rýchlostná konštanta chemickej reakcie. Jeho hodnotu možno získať okrem použitia Arrheniusovej rovnice uplatňovaním zákona o rýchlosti. Predstavuje počet kolízií medzi časticami produkovanými reakciou za sekundu.
Do
Je to takzvaný predponponenciálny faktor, ktorý predstavuje frekvenciu kolízií medzi molekulami činidla s vhodnou geometrickou orientáciou, ktorá môže alebo nemusí vyvolať chemickú reakciu. Ak má teplotná variácia malej veľkosti, zvyčajne sa považuje za konštantnú. Tento faktor má svoj vlastný vzorec:
A = z ρ
Kde z je známy ako frekvenčný alebo kolízny faktor a ρ geometrický alebo stérický faktor, ktorý naznačuje relatívnu orientáciu molekúl v kolíznom bode. Konštanta A má rovnaké jednotky ako rýchlosť konštanty. V prípade, že neexistuje žiadna aktivačná energia, rozsah A sa bude rovnať veľkosti K.
Ado
Je to aktivačná energia, ktorá predstavuje prahovú energiu pred dosiahnutím prechodného statu.
Aktivačná energia má jednotku KJ/MOL. Ale vo výpočtoch sa j/mol používa ako jednotka. Najmenší (-) znamenie, ktoré predchádza Edo, Slúži, čo naznačuje, že jeho zvýšenie spôsobuje zníženie reakčnej rýchlosti, ako aj jeho zníženie spôsobuje zvýšenie reakčnej rýchlosti.
Môže vám slúžiť: plynová chromatografiaRt
Predstavuje priemernú kinetickú energiu. Medzitým R je univerzálna konštanta plynov, ktorá je jednou z najpoužívanejších hodnôt 8.31 j · k-1· Mol-1. A t je absolútna teplota vyjadrená v Kelvin (k).
a
Je to základ prírodných alebo neperiánskych logaritmov, má hodnotu 2.71828.
a-EA/RT
Je to frakcia reagujúcich molekúl s rovnakou alebo nadmernou energiou vo vzťahu k aktivačnej energii.
Žiadosti
Väčšina aplikácií Arheniusovej rovnice pochádza z použitia pri určovaní rýchlosti konštanty; a rozšírenia, rýchlosť reakcie, ako aj jej aktivačná energia.
Napríklad bol vyvinutý chemický model na základe rovnice Arrhenius, ktorá môže predpovedať vlastnosti materiálov ako ich zmenu teploty, ktoré sa uplatňujú v oblasti geológie, výstavby, inžinierstva materiálov a v oblasti potravín.
Uplatňovala sa, aj keď s určitou kritikou, Arrheniusova rovnica v kinetike reakcií v tuhom stave. Používa sa tiež na charakterizáciu reakcií rastlín na vodný stres.
Rovnica Arenhius slúžila ako základ pre vytvorenie matematického modelu, ktorý kvantifikuje účinok teploty na životnosť niklových kovových hydridových buniek alebo batérií.
Podobne, na základe Arrheniusovej rovnice, bola založená miera rozkladu odpadu ošípaných a olej na varenie, pod rôznymi obsahmi vlhkosti.
Vyriešené cvičenia
Cvičenie 1
Aká je aktivačná energia reakcie, ak sa zistí, že jeho rýchlosť konštanta sa strojnásobí, keď teplota stúpa zo 600 k na 610 K?
Môže vám slúžiť: kyselina fenoxyaktová: syntéza, postup, použitie, rizikáPočnúc Arrheniusovou rovnicou:
k = a · e-EA/RT
Vyčistíme faktor A:
A = k1 (e-EA/RT1)
Ale pretože máme dve teploty, T1 a t2, Budú dve rýchlostné konštanty: K1 a k2. Faktor A sa nemení, takže ho môžeme porovnať za druhú teplotu:
klimatizovať1 (e-EA/RT1) = k2 (e-EA/RT2)
A zúčtovanie edo budeme mať:
Ado = R (ln k2/k1) / (1 / t1 - 1/t2)
Ako čo2 je trikrát väčší ako k1,
klimatizovať2 / k1 = 3
ln (3) = 1.099
A na druhej strane:
1 / t1 = 1/600 K = 1.66 x 10-3 Klimatizovať-1
1 / t2 = 1/610 K = 1.64 x 10-3 Klimatizovať-1
Výmena potom:
Ado = (8.31 j · k-1· Mol-1) (1.099) / (1.66 x 10-3 Klimatizovať-1 - 1.64 x 10-3 Klimatizovať-1)
= 456.5 kJ · mol-1
Cvičenie 2
Pri reakcii na plynnú fázu sa aktivačná energia rovná 103 kJ/mol a rýchlostná konštanta je 0.085 min-1. Vypočítajte rýchlostnú konštantu pri 323 K.
Z predchádzajúceho výrazu vyčistíme ln k2/k1:
ln k2/k1 = (Edo/R) (1 /t1 - 1/t2)
Rozvoj správnej časti rovnice:
ln k2/k1 = (103.000 j · mol-1 / 8.31 j · k-1· Mol-1) (1/273 K - 1/323 K)
ln k2/k1 = 6.99
Berúc antilogaritmy:
klimatizovať2/k1 = 1.086
klimatizovať2 = (k1) (1.086)
= (0.085 min-1) (1.086)
= 0.092 min-1
Odkazy
- Whitten, Davis, Peck & Stanley. (2008). Chémia. (8. vydanie.). Učenie sa.
- Walter J. Moore. (1963). Fyzikálna chémia. V chemickej kinetike. Štvrté vydanie, Longmans.
- Irán. Levine. (2009). Princípy fyzikálneho spôsobu. Šieste vydanie. MC Graw Hill.
- Wikipedia. (2020). Arrheniusova rovnica. Zdroj: In.Wikipedia.orgán
- Guenevieve del Mundo a kol. (10. september 2020). Arrheniusova rovnica. Získané z: Chem.Librettexts.orgán
- Clark Jim. (2013). Rýchlostné konštanty a Arrheniusova rovnica. Získané z: Chemguide.co.Uk
- Redaktori Enyclopaedia Britannica. (2020). Arrheniusova rovnica. Získané z: Britannica.com
- HelMestine, Anne Marie, PH.D. (28. augusta 2020). Vzorec a príklad Arrheniusovej rovnice. Zotavené z: Thoughtco.com

