Doména a protichodné funkcie (s príkladmi)

Koncepty doména a rozpory funkcie Bežne sa učia v kurzoch výpočtu vyučovaných na začiatku univerzitnej kariéry.

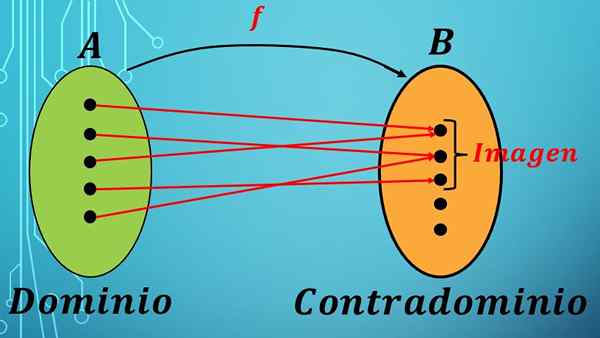
Pred definovaním domény a rozporu by ste mali vedieť, čo je funkcia. Funkcia F je korešpondenčný zákon (pravidlo) medzi prvkami dvoch sád.

Celý zvolený prvky sa nazýva doména funkcie a súbor, ku ktorej sa tieto prvky odosielajú prostredníctvom F, sa nazýva kontradominium.

V matematike je funkcia s doménou A a Contradominium B označená výrazom F: A → B.

Predchádzajúci výraz hovorí, že prvky množiny A sa odosielajú na nastavenie B podľa zákona o korešpondencii f.

Funkcia priraďuje každý prvok množiny jednému prvku množiny B.

Doména a rozpor

Vzhľadom na skutočnú funkciu skutočnej premennej f (x) musí byť doménou funkcie všetky tie reálne čísla tak, že pri vyhodnotení vo F je výsledkom skutočné číslo.

Všeobecne platí, že v rozpore funkcie je sada skutočných čísel n. Rozpor sa tiež nazýva príchod alebo kodominium sada funkcie F.

Rozpor funkcie je vždy r?

Nie. Pokiaľ sa funkcia podrobne nepreštuduje, súbor skutočných čísel N sa zvyčajne považuje za rozpor.

Ale akonáhle je funkcia študovaná, vhodnejšia sada sa dá považovať za protichodné, čo bude podskupina R.

Príslušný súbor uvedený v predchádzajúcom odseku sa zhoduje s obrazom funkcie.

Definícia obrazu alebo rozsahu funkcie F sa vzťahuje na všetky hodnoty, ktoré pochádzajú z vyhodnotenia prvku domény v F.

Príklady domény a rozporu

V nasledujúcich príkladoch, ako vypočítať doménu funkcie a jej obraz je ilustrovaný.

Príklad 1

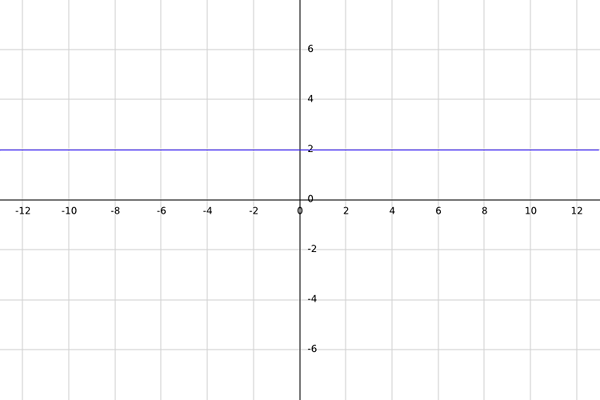
Nech f je skutočná funkcia definovaná f (x) = 2.

M -domain f je všetky skutočné čísla tak, že pri ich hodnotení vo F je výsledkom skutočné číslo. Rozpor na túto chvíľu sa rovná R.

Pretože daná funkcia je konštantná (vždy rovná 2), musí bez ohľadu na to, aké skutočné číslo je vybrané, pretože pri hodnotení vo F sa výsledok bude vždy rovnať 2, čo je skutočné číslo.

Preto je doménou danej funkcie všetky reálne čísla; to znamená, a = r.

Teraz, keď je už známe, že výsledok funkcie sa vždy rovná 2, obraz funkcie je iba číslo 2, preto je rozpor funkcia nanovo definovaný ako b = img (f) = 2.

Preto f: r → 2.

Príklad 2

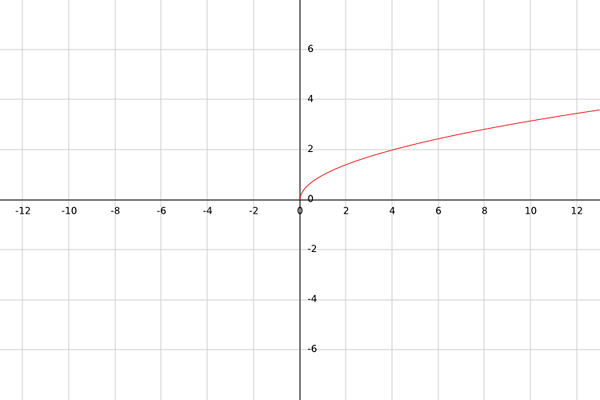
Nech g je skutočná funkcia definovaná g (x) = √x.

Pokiaľ nie je známy obraz G, kontradominium G je b = r.

S touto funkciou by sa malo zohľadniť, že druhé korene sú definované iba pre negatívne čísla; to znamená pre čísla väčšie alebo rovnaké ako nula. Napríklad √-1 nie je skutočné číslo.

Preto musí byť zvládnutie funkcie G všetky čísla väčšie alebo rovnaké ako nula; to znamená x ≥ 0.

Preto a = [0,+∞).

Na výpočet rozsahu by sa malo poznamenať, že akýkoľvek výsledok g (x), pretože je to druhý koreň, bude vždy väčší alebo rovný. To znamená, b = [0,+∞).

Na záver G: [0,+∞) → [0,+∞).

Príklad 3

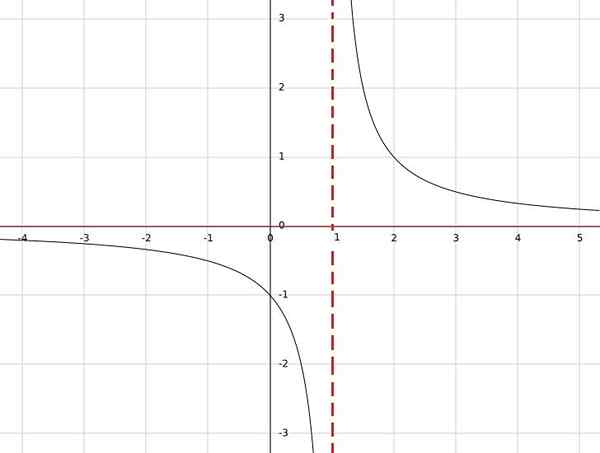
Ak máte funkciu H (x) = 1/(x-1), táto funkcia nie je definovaná pre x = 1, pretože v menovateľovi by sa získal nula a delenie nulou nie je definované.

Na druhej strane, pre akúkoľvek inú skutočnú hodnotu bude výsledkom skutočné číslo. Preto sú doména všetky reais s výnimkou jedného; to znamená a = r \ 1.

Rovnakým spôsobom je zrejmé, že jediná hodnota, ktorú nie je možné získať v dôsledku.

Obrázok funkcie je preto sada všetkých reais s výnimkou nuly, potom sa považuje za kontrastominium b = r 0.

Na záver H: R \ 1 → R \ 0.

Pozorovanie

Doména a obraz nemusia byť rovnaké, ako je uvedené v príkladoch 1 a 3.

Ak je funkcia grafom v karteziánskej rovine, doména je znázornená osou X a protichodné alebo rozsah je znázornené osi y.