120 deliteľov

Ten 120 deliteľov Sú to všetky tie čísla, ktoré to presne rozdelia. Tieto čísla sú nasledujúce:

Divisory 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Tiež protiklady k tomuto súboru čísel, to znamená, že negatívy sú 120 deliacich, pretože rozdelenie je presné. 120 má 16 pozitívnych celých deliacich a mnoho ďalších negatívov.

Existuje niekoľko spôsobov, ako nájsť deliteľov čísla. Ak to nie je príliš veľké, môžete použiť násobenie tabuliek (pre čísla menej ako 100) a overiť, v ktorých tabuľkách sa objaví príslušné číslo. Napríklad 12 sa objaví v tabuľkách po 2, 3, 4 a 6, a to sú ich deliaci, spolu s 1 a rovnakými 12.

Číslo sa dá rozdeliť aj na jeho hlavné faktory, uplatňovať pravidlá deliteľnosti a vynásobiť faktory. Ale musíte byť opatrní, aby ste neprešli žiadnym deliacim prehliadaným.

Pretože 120 je väčší ako 100, nie je priamo v násobkových tabuľkách, nie je však príliš namáhavá na nájdenie svojich 16. Platný postup pre všetky čísla je zobrazený okamžite pomocou veľmi jednoduchých tabuliek.

Koľko deliteľov je 120?

Po prvé, zistí sa počet deliteľov 120. Existuje vzorec, ktorý vám umožní vedieť, koľko máte, hoci to nehovorí, čo sú.

Zložené čísla, ako napríklad 120, možno vyjadriť ako produkt prvých čísel alebo ich právomoci. Volanie n na akékoľvek číslo zloženia:

N = aⁿ ∙ B^m ∙ c^p ... r^{klimatizovať}

Môže vám slúžiť: Vzťahy proporcionality: koncept, príklady a cvičenia

Čísla a, b, c ... r sú prvotné čísla a hodnoty n, m, p, ... k, príslušné sily. Rozklad v hlavných faktoroch 120 je nasledujúci:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

Týmto spôsobom je 120 produktom faktorov:

120 = 2³ ∙ 3 ∙ 5

Vzorec na výpočet počtu deliteľov n

Počet deliteľov = (n +1) × (m +1) × (p +1)… × (k +1)

Teraz sa používa vzorec na 120. Od rozkladu vo faktoroch musíte:

n = 3 (je sila 2)

M = 1 (3 je zvýšené na 1: 3¹ = 3)

P = 1 (5 sa tiež javí ako zvýšené na 1)

S týmito hodnotami:

Počet deliteľov 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Tento výsledok sa zhoduje so začiatkom začiatku: 120 má 16 deliteľov. Okrem toho je už známe, že 2, 3 a 5 sú deliteľmi 120, ako aj 10, pretože akékoľvek číslo skončené v 0 je deliteľné 10. Postup na ich nájdenie všetkých je okamžite zobrazený.

Výpočet deliteľov 120

Robí sa pomocou faktorov vypočítaných v predchádzajúcej časti. Tam sa zistilo, že 2 je hlavným faktorom s exponentom 3 a 3 je ďalší bratrancový faktor, s exponentom 1. S týmito informáciami je vytvorená nasledujúca tabuľka:

Všimnite si, že právomoci 2 začínajú v 2⁰ a skončiť v 2³, čo je faktor, ktorý vzniká pri rozklade 120. Pamätajte, že 2⁰ a 3⁰ Obidve sa rovnajú 1 (akékoľvek číslo vysoké do 0 je 1). Pre faktor 3 sa začína v 3⁰ Do 3¹, Od 3¹ = 3.

Ďalej je tabuľka vyplnená produktom čísel v červenej farbe, ako je to znázornené tu:

Môže vám slúžiť: Multiplikatívna inverzia: Vysvetlenie, príklady, vyriešené cvičenia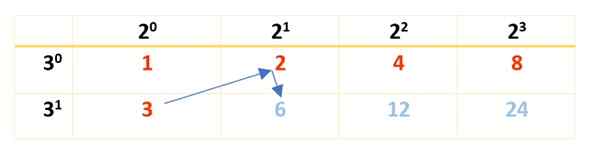

Všetky červené a modré čísla sú 120 deliteľov, ale sotva je 8. Aby sme našli zostávajúce, je prasknutie novej tabuľky, delení už boli získané v prednom rade a faktor, ktorý sa ešte musí zohľadniť, je napísaný: 5, s ich právomocami v prvom stĺpci, vľavo, ako je tento:

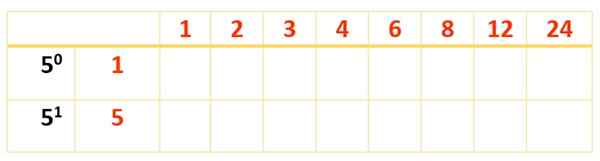
Teraz je tabuľka vyplnená produktmi čísel v červenej farbe, ako sa to stalo pri prvej tabuľke:

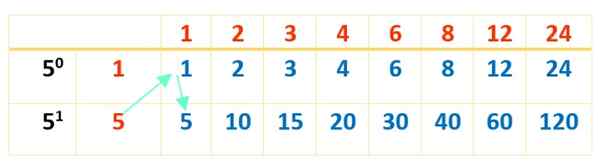
A nakoniec sa objaví 16 deliteľov 120 v modrej farbe. Tabuľky sú vynikajúcou pomocou pre operácie, ktoré sa majú vykonať v poriadku, a teda nie 120 deliteľ.

Vyriešené cvičenia

Postup na nájdenie všetkých deliteľov čísla je zhrnutý nasledovne:

1. Rozdeliť číslo na hlavné faktory.
2. Vypočítajte počet deliteľov pomocou vzorca.
3. Postavte potrebné tabuľky na nájdenie deliteľov. Ak má číslo dva faktory, je tabuľka dostatočná, ak máte tri faktory, musia sa urobiť dve tabuľky, ako v prípade 120.

Cvičenie 1

Nájdite všetkých deliteľov 288.

Riešenie

288 sa rozkladá do hlavných faktorov:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

288 je napísané takto:

288 = 2⁵ ∙ 3²

Okamžite je počet deliteľov 288 až:

Počet deliteľov = (n +1) × (m +1) × (p +1)… × (k +1)

Z rozkladu v hlavných faktoroch sa poznamenáva, že n = 5 a m = 2, potom:

Divisory 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Existuje 18 deliteľov a keďže existujú iba dva faktory, stačí iba s jednou tabuľkou:

Môže vám slúžiť: Charakteristiky obdĺžnika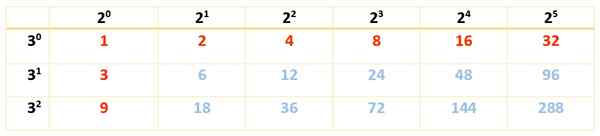

Divisory 288 sú čísla v červenej a modrej farbe:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Môžu sa rýchlo skontrolovať pomocou kalkulačky.

Cvičenie 2

Nájdite deliacich 350

Riešenie

350 rozkladá:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

350 možno napísať ako produkt troch faktorov:

350 = 2 ∙ 5²∙ 7

Ďalším krokom je výpočet toho, koľko deliteľov má prostredníctvom vzorca:

Počet deliteľov = (n +1) × (m +1) × (p +1)… × (k +1)

S n = 1, m = 2, p = 1

Divisory 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Pretože 350 vyžaduje tri faktory, musia sa predložiť dve tabuľky. Prvý sa robí s 2 a 5², Ale dá sa to urobiť aj s 2 a 7 alebo so 7 a 5², Podľa preferencie, pretože vo všetkých formách je konečný výsledok rovnaký:

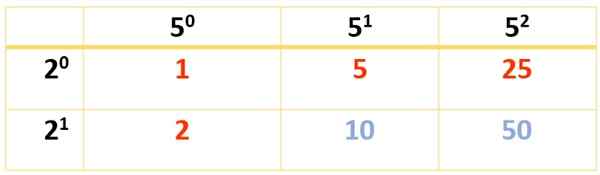
Získava sa 6 deliteľov. Ostatní sa objavia pomocou tejto druhej tabuľky:

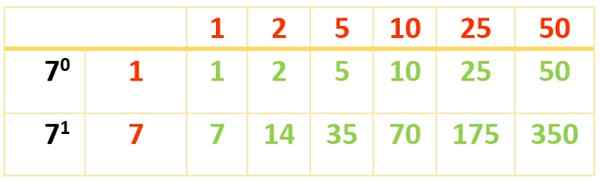
Divisors z 350 sú:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350