Syntetické delenie

Vysvetlíme, čo je syntetické delenie, metóda na to, príklady a cvičenia vyriešené.

Čo je to syntetické delenie?

Ten Syntetické delenie Je to jednoduchý spôsob, ako rozdeliť polynóm P (x) jednou z foriem d (x) = x - c - c. Napríklad polynóm p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) môže byť reprezentovaný ako násobenie dvoch najjednoduchších polynómov (x+1) a (x⁴ + 2x³).

Je to veľmi užitočný nástroj, pretože okrem toho, že nám umožňuje rozdeliť polynómy, umožňuje tiež vyhodnotiť P (x) polynóm v ľubovoľnom čísle C, čo nás zase naznačuje, či je toto číslo nula alebo nie z polynóm.

Vďaka algoritmu divízie vieme, že ak máme dva P (x) a d (x) polynóm (x) + r (x), kde r (x) je nula alebo je menšia ako q (x). Tieto polynómy sú známe ako kvocient a zvyšky alebo odpočinok.

V prípadoch, keď je polynóm d (x) vo forme x - c, syntetické rozdelenie nám dáva krátku cestu, aby sme zistili, kto sú Q (x) a r (x).

Metóda syntetického delenia

Nech p (x) = a_nXⁿ+do_N-1X^N-1+… +A₁x+a₀ polynóm, ktorý chceme rozdeliť a D (x) = x-c deliteľ. Rozdeliť metódou syntetického rozdelenia postupujeme nasledovne:

1- V prvom riadku píšeme koeficienty p (x). Ak sa neobjaví akýkoľvek výkon X, umiestnime nulu ako jeho koeficient.

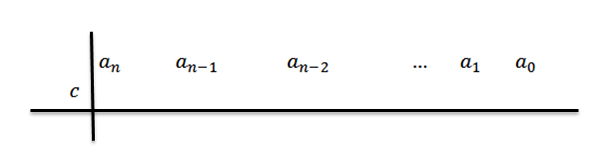
2- v druhom rade, vľavo od a_n Umiestnime C a kreslenie čiar, ako je to znázornené na nasledujúcom obrázku:

3- Znížíme vedúci koeficient do tretieho riadku.

Môže vám slúžiť: Eulerova metóda: Aké je použitie postupu a cvičení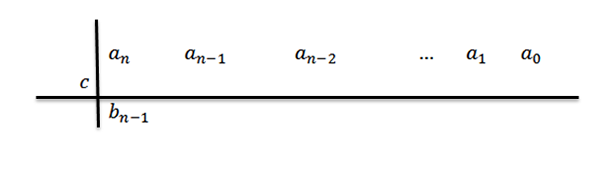

V tomto výraze B_N-1= a_n

4- vynásobíme C vedúcim koeficientom B_N-1 A napíšeme výsledok v druhom riadku, ale stĺpec vpravo.

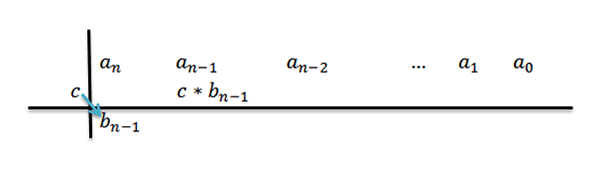
5- Pridáme stĺpec, v ktorom píšeme predchádzajúci výsledok a výsledok je uvedený pod uvedenú sumu. To znamená v rovnakom stĺpci tretí riadok.

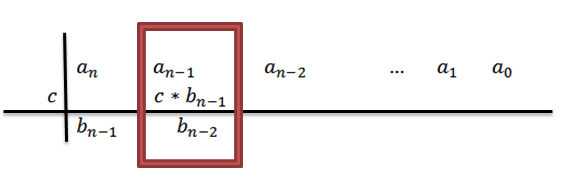
Pridaním, v dôsledku toho máme_N-1+c*b_N-1, Komu pre pohodlie zavoláme B_N-2

6- Vynásobíme C o predchádzajúci výsledok a výsledok napíšeme v druhom riadku.

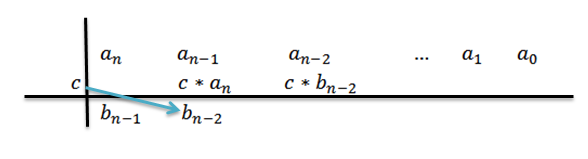
7- opakujeme krok 5 a 6, kým nedosiahneme koeficient₀.

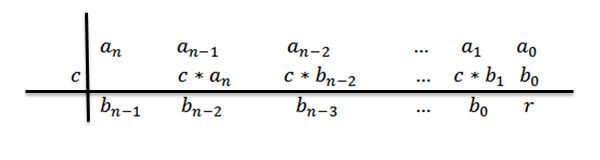
8- Píšeme odpoveď, to znamená kvocient a zvyšky. Keď robíme rozdelenie polynómu triedy N medzi polynómom 1. stupňa, máme, že kvocientom by bol stupeň N-1.

Koeficienty kvocientového polynómu budú čísla tretieho radu, s výnimkou posledného, ​​ktorý bude zvyškový polynóm alebo zvyšok divízie.

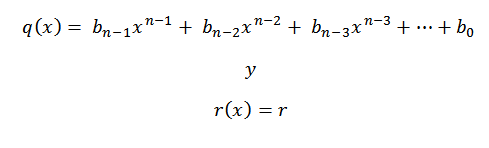
Vyriešené cvičenia

Príklad 1

Vytvorte nasledujúce rozdelenie metódou syntetického delenia:

(X⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Riešenie

Najprv napíšeme dividendové koeficienty nasledovne:

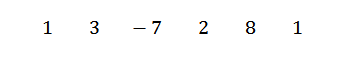
Potom napíšeme C na ľavú stranu, v druhom riadku spolu s riadkami divízie. V tomto príklade C = -1.

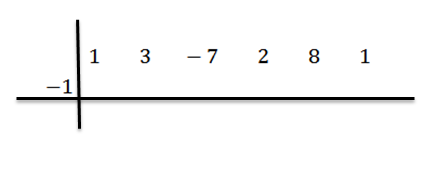
Znížíme vedúci koeficient (v tomto prípade B_N-1 = 1) a vynásobíme to -1:

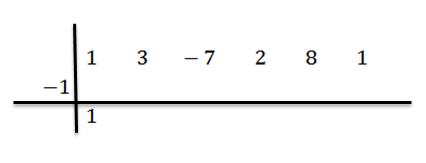
Jeho výsledok sme napísali napravo v druhom riadku, ako je uvedené nižšie:

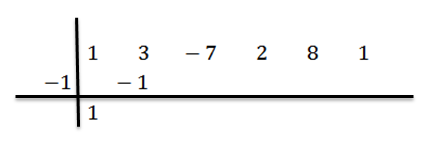
Pridáme čísla druhého stĺpca:

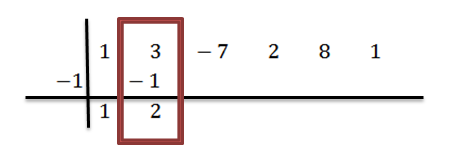
Vynásobíme 2 po -1 a výsledok napíšeme do tretieho stĺpca, druhý riadok:

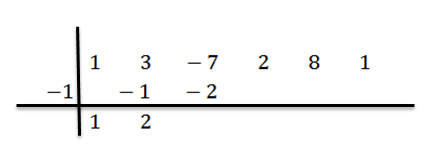
Pridáme do tretieho stĺpca:

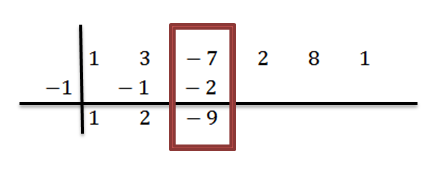
Pokračujeme analogicky, kým nedosiahneme posledný stĺpec:

Môže vám slúžiť: predvolený a nadmerný prístup: Čo je a príklady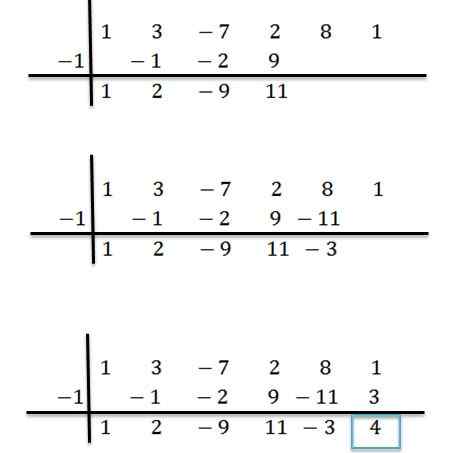

Máme teda, že posledné získané číslo je zvyšok divízie a zostávajúce čísla sú koeficienty kvocientového polynómu. Toto je napísané takto:

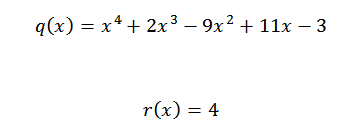
Ak chceme overiť, či je výsledok správny, stačí overiť, či je splnená nasledujúca rovnica:

P (x) = q (x)*d (x) + r (x)

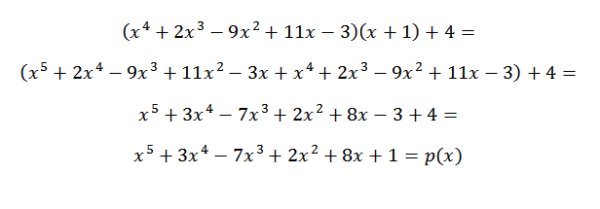
Môžeme teda overiť, či je získaný výsledok správny.

Príklad 2

Vykonajte nasledujúce polynómové rozdelenie metódou syntetického delenia:

(7x³-x+2): (x+2)

Riešenie

V tomto prípade máme tento výraz X² Nezjaví sa, takže ako jeho koeficient napíšeme 0. Polynóm by teda zostal ako 7x³+0x²-x+2.

Píšeme vaše koeficienty do riadku, to znamená:

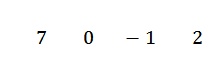
Píšeme hodnotu C = -2 na ľavú stranu v druhom riadku a nakreslíme riadky divízie.

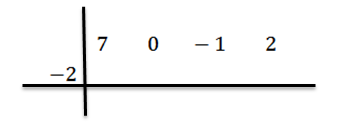
Znížíme vedúci koeficient B_N-1 = 7 a vynásobíme ho -2 a zapisujeme jeho výsledok v druhom riadku napravo.

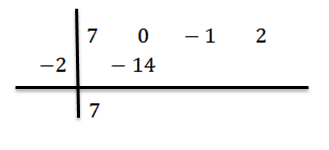
Pridávame a pokračujeme, ako už bolo vysvetlené, až kým nedosiahneme posledný termín:

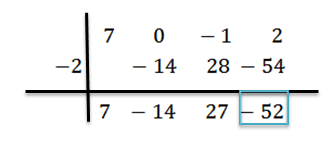
V tomto prípade je zvyšok r (x) = -52 a získaný kvocient je q (x) = 7x²-14x+27.

Príklad 3

Ďalším spôsobom, ako použiť syntetické delenie, je nasledujúci.

Pre algoritmus divízie môžeme napísať polynóm p (x) nasledovne:

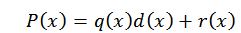
V tomto výraze sú q (x) a r (x) kvocient a zvyšok, v danom poradí. Teraz, ak d (x) = x-c, pri hodnotení C v polynóme nájdeme nasledujúce:

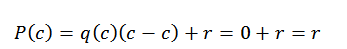
Z tohto dôvodu zostáva len nájsť R (x) a my to môžeme urobiť vďaka syntetickému rozdeleniu.

Napríklad máme polynomiálny p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 a chceme vedieť, aká je jej hodnota pri hodnotení jej na x = 5. Za týmto účelom vykonávame rozdelenie medzi p (x) a d (x) = x -5 metódou syntetického delenia:

Môže vám slúžiť: axiálna symetria: Vlastnosti, príklady a cvičenia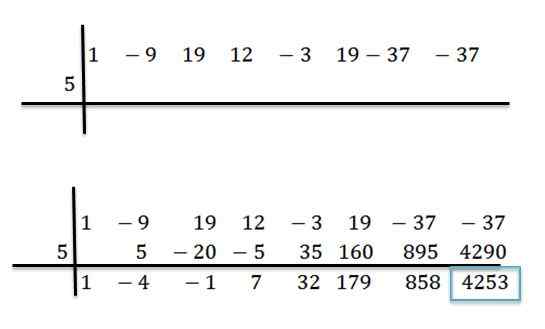

Po vykonaní operácií vieme, že dokážeme písať p (x) takto:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x² +179x + 858)*(x-5) + 4253

Preto pri hodnotení musíme:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Ako vidíme, je možné použiť syntetické delenie na nájdenie hodnoty polynómu pri jeho hodnotení v C namiesto jednoduchého nahradenia C za x. 

Ak sa pokúsime vyhodnotiť p (5) tradičným spôsobom, potrebovali by sme niektoré výpočty, ktoré sa zvyčajne stanú únavnými.

Príklad 4

Algoritmus delenia pre polynómy sa tiež stretáva pre polynómy s komplexnými koeficientmi a v dôsledku toho máme, že metóda syntetického delenia funguje aj pre tieto polynómy pre tieto polynómy. Ďalej uvidíme príklad.

Použijeme metódu syntetického delenia, aby sme ukázali, že z = 1+ 2i je nula polynómu p (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). To znamená, že zvyšok divízie p (x) medzi d (x) = x - z sa rovná nule.

Postupujeme ako predtým: V prvom riadku píšeme koeficienty P (x), potom v druhom píšeme z a nakreslime riadky divízie.

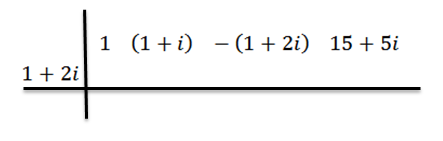
Robíme rozdelenie ako predtým, to znamená:

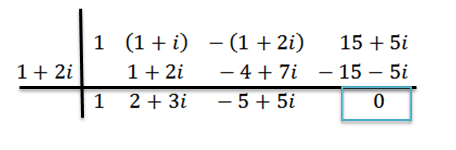
Vidíme, že zvyšok je nula; Preto sme dospeli k záveru, že Z = 1+ 2i je nula P (x).

Odkazy

1. Baldor, Aurelio. Algebra. Redakčná skupina Patria.
2. Demana, Waits, Foley & Kennedy. Prekácu: grafické, numerické, algebraické. Pearson Vzdelanie.