Uhlové posun

Čo je uhlové posun?

On Uhlové posun Je to zmena alebo variácia v uhlovej polohe, že objekt v rotácii, zvyčajne meraný v radiánoch alebo akékoľvek iné opatrenie uvedené na zákruty, ako sú známky alebo revolúcie.

Keď sa objekt otáča okolo pevnej osi, jeho uhlové posun sa určí meraním uhla zametaného čiarou, ktorá prechádza cez akýkoľvek bod tela, ktorý pretína os rotácie, to znamená radiálnu čiaru.

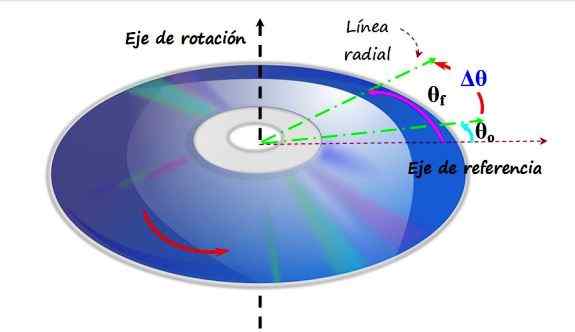Kompaktný disk alebo CD sa točí v antihoranantnom smere okolo vertikálnej osi rotácie. Pri prechode z uhla θo na θf sa hovorí, že zažil uhlové posunutie. Zdroj: f. Zapata.

Na hornej postave je CD, ktoré sa otáča v anti -horskom smere, čo je jej os rotácie vertikálnou osou. Referenčná os sa umiestni na rovinu CD, čo zodpovedá uhlu 0 radiánov alebo 0. Zelená čiara je radiálna čiara, ktorá spočiatku tvorí uhol 9_ani S odkazom. Toto je vaša počiatočná pozícia.

Neskôr sa zelená čiara presunie do novej polohy nazývanej 9_F, A skúsenosť, ktorá sa nazýva δθ, je jednoducho:

Δθ = 9_F - 9_ani

Akýkoľvek bod P Cd zažíva rovnaké uhlové posun v určitom časovom intervale, s výnimkou stredu, kde je os rotácie prechádza a zostáva v pokoji.

Vzorce a rovnice

Existuje objekt, ktorý sa točí okolo pevnej osi alebo ktorý opúšťa obrazovku na čítačku. A v ňom je bod P, umiestnený vo vzdialenosti r osi rotácie a popisuje obvody Rádiu R.

Toto je vidieť na nasledujúcom obrázku, ktorý ukazuje rezný objekt, videný v rozpore s ihlami s hodinami. Dôvodom je v uhlovej polohe 9, meraná z referenčnej osi, ktorá je v tomto prípade horizontálna os.

Môže vám slúžiť: Aditívny princíp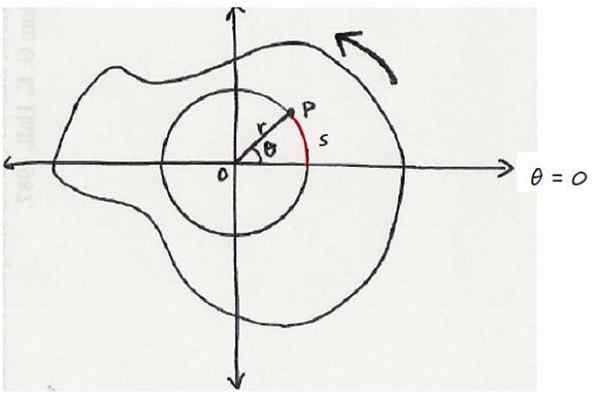Objekt, ktorý sa otáča v anti -horskom zmysle. Os rotácie vyjde kolmá na obrazovku. Zdroj: Wikimedia Commons.

Konvenciou, k rotácii v antihorariálnom zmysle je priradený pozitívny zmysel, zatiaľ čo rotácia v harmonograme má negatívne znamenie.

Keď bod P prisahá uhol 9, súčasne prechádza oblúk. Pretože 9 je centrálny uhol, pretože jeho vrchol zaberá stred obvodu, splní sa to:

S 9 vyjadrenými v Radianoch.

Uhlové posun je:

Δθ = 9_Konečný  - 9_{počiatočný}

Napríklad, ak P začal s 9_{počiatočný} = 0 rad a potom je v 9_Konečný = 0.8 RAD, jeho uhlové posunutie je od:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Ostatné body objektu môžu zaberať rôzne uhlové polohy, ale všetky zažívajú rovnaké uhlové posun. Avšak najodľahlejšie častice zo stredu cestujú väčšie vzdialenosti, pretože s = r⋅θ.

Zmerať

Pri rotácii je bežné nájsť uhly merané v radiánoch, ale nachádzajú sa aj v stupňoch a revolúciách alebo zákrutách. Pri riešení problémov je potrebné presunúť sa z týchto jednotiek na Radianes.

1 Revolúcia je rovnocenná s úplným zákrutou, to znamená, že keď sa úplne rozbije, otočil sa 360 ° a tieto sú rovnocenné s Radians 2π, pretože v takom prípade bod prešiel oblúkom rovným 2πr:

Ale zjednodušenie, predchádzajúcu rovnocennosť možno vyjadriť takto:

π radiany = 180 °

Ako sa vypočíta uhlové posun?

Uhlové posun sa môže vypočítať analogicky s tým, ako sa posunutie pohybu vypočíta v rozmere, podľa určitého modelu pohybu. Z tohto dôvodu je priemerná uhlová rýchlosť definovaná ako uhlové posunutie δθ v danom časovom intervale ΔT:

Kde je priemerná uhlová rýchlosť označená ako Ω_m a je uvedený v Radians/S v jednotkách medzinárodného systému, ak.

Môže vám slúžiť: Ako získať uhol trojuholníka? (Príklad)

Okamžitá uhlová rýchlosť je limit priemernej uhlovej rýchlosti, keď ΔT → 0:

To znamená, že je to prvý odvodený z uhlovej polohy vzhľadom na čas. Na druhej strane je možné definovať uhlové zrýchlenie, označené ako a, čo je ekvivalentné derivátu alebo rýchlosti zmeny uhlovej rýchlosti vzhľadom na čas:

Ktoré možno interpretovať aj ako druhý odvodený z uhlovej polohy vzhľadom na čas.

Dôležitá vec je, že dva pohybové modely sa dajú stanoviť v analógii s priamymi pohybmi, pretože hoci sa rotácie vykonávajú v rovine, stačí jediná uhlová súradnica na stanovenie polohy akéhokoľvek bodu objektu.

Rovnomerný pohyb kruhu

V rovnomernom pohybe kruhu je uhlová rýchlosť konštantná, to znamená, že priemerná uhlová rýchlosť sa rovná okamžitej uhlovej rýchlosti. Keďže uhlové zrýchlenie a je rovné 0, môžete pre pozíciu pre túto funkciu času napísať nasledujúcu rovnicu:

9 = 9_ani + Ωt

Kde 9_ani Je to počiatočná poloha mobilu.

Rovnomerne zrýchlený kruhový pohyb

V tomto prípade je uhlové zrýchlenie a je konštantné a analogicky s rovnomerne rozmanitým priamym pohybom je možné napísať nasledujúce rovnice:

• 9 = 9_ani + Ω_ani T + ½ αt²
• Ω = Ω_ani + αT 
• Ω² = Ω_ani² + 2a ∙ δθ

Cvičenie

Prvé cvičenie

Dá sa predpokladať, že Zem je tuhý objekt, ktorý sa točí na pevnej osi a že jej rotácia je takmer jednotná. V časovom intervale Δt = 12 h Nájdite:

a) uhlové posunutie Zeme

b) Vaša uhlová rýchlosť

c) uhlové zrýchlenie v tomto časovom intervale.

Roztok

S vedomím, že za 24 hodín sa Zem úplne otočí okolo svojej osi, za 12 hodín budete mať polovicu kola, to znamená, π radiany. Ak sa považuje za tú časť 9_{počiatočný} = 0 RAD, potom jeho uhlové posun je:

Môže vám slúžiť: Multiplikatívny princíp: Techniky počítania a príklady

Δθ = π radiány

Riešenie B

Pretože rotácia je rovnomerná, uhlová rýchlosť je kvocientom medzi uhlovým posunom a časom, navyše 1 hodinu = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Riešenie c

Uhlové zrýchlenie je neplatné, pretože rotácia Zeme je rovnomerná.

Druhé cvičenie

Juan spustil vzdialenosť 35 metrov na kruhovej atletickej dráhe, ktorej polomer sa rovná 7 metrov. Vypočítajte uhlové vytesnenie, ktoré Juan urobil.

Riešenie

Pretože je známa vzdialenosť prejdeného oblúka a polomer obvodu, je možné aplikovať druhý vzorec, aby sa poznal uhlové posun, ktorý uskutočnil Juan. Pomocou vyššie uvedeného vzorca musíte 9 = 35/7 = 5 radiánov.

Tretie cvičenie

Ak má Mario vo svojom vozidle, polovica kruhovej závodnej dráhy, aké je uhlové posun, ktorý urobil Mario?

Riešenie

V tomto cvičení sa bude uplatňovať prvý vzorec. Pretože je známe, že Mario prešiel polovicou trate, možno predpokladať, že začal závod v uhle 0 ° a keď dosiahol polovicu obvodu, prešiel 180 °. Odpoveď je preto 180 ° -0 ° = 180 ° = π radiány.

Štvrté cvičenie

Maria má kruhový bazén. Váš pes beží okolo bazéna a cestuje vo vzdialenosti 18 metrov. Ak je polomer bazénu 3 metre, aké je uhlové vytesnenie uskutočnené Márie domáceho maznáčika?

Riešenie

Pretože bazén je kruhový a polomer je známy, môžete pokračovať v použití druhého vzorec.

Je známe, že polomer sa rovná 3 metre a vzdialenosť prevezená domácim miláčikom sa rovná 18 metrov. Preto sa vykonané uhlové posunutie rovná 9 = 18/3 = 6 radiánov.

Odkazy

1. Katz, D. 2013. Fyzika pre vedcov a inžinierov. Základy a spojenia. Učenie sa.
2. Rex, a. 2011. Základy fyziky. Pearson.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
5. Tipler, P. (2006). Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil.