Koľko riešení má kvadratická rovnica?

Kvadratická rovnica alebo rovnica druhého stupňa môžu mať nulu, jedno alebo dve skutočné riešenia v závislosti od koeficientov, ktoré sa objavujú v uvedenej rovnici. Ak pracujete na zložitých číslach, môžete povedať, že každá kvadratická rovnica má dve riešenia.

Na spustenie kvadratickej rovnice je to rovnica formulára Ax²+bx+c = 0, kde a, b a c sú reálne čísla a x je premenná.

Hovorí sa, že X1 je riešením predchádzajúcej kvadratickej rovnice, ak je pri výmene x za X1 splnená rovnica, to znamená, ak (x1) ²+b (x1)+c = 0.

Ak máte napríklad rovnicu x²-4x+4 = 0, potom x1 = 2 je roztok, pretože (2) ² (2) +4 = 4-8+4 = 0.

Naopak, ak sa nahradí x2 = 0, získa sa (0) ²-4 (0) +4 = 4 a ako 4 ≠ 0, potom x2 = 0 nie je riešením kvadratickej rovnice.

Riešenia kvadratickej rovnice

Počet riešení kvadratickej rovnice sa môže oddeliť v dvoch prípadoch, ktoré sú:

1.- V skutočných číslach

Pri práci so skutočnými číslami môžu mať kvadratické rovnice:

-Nulové riešenia: To znamená, že neexistuje žiadne skutočné číslo, ktoré by spĺňa kvadratickú rovnicu. Napríklad rovnica daná x²+1 = 0, neexistuje žiadne skutočné číslo, ktoré by splnilo uvedenú rovnicu, pretože obidve x² sú väčšie alebo rovné nule a 1 sú väčšie prísne ako nula, takže jej súčet bude väčší Prísny ako nula.

-Opakované riešenie: Existuje jediná skutočná hodnota, ktorá vyhovuje kvadratickej rovnici. Napríklad jediné riešenie rovnice x²-4x+4 = 0 je x1 = 2.

-Dve rôzne riešenia: Existujú dve hodnoty, ktoré uspokojujú kvadratickú rovnicu. Napríklad x²+x -2 = 0 má dve rôzne roztoky, ktoré sú x1 = 1 a x2 = -2.

2.- V zložitých číslach

Pri práci s komplexnými číslami majú kvadratické rovnice vždy dve riešenia, ktoré sú Z1 a Z2, kde Z2 je konjugát Z1. Okrem toho ich možno klasifikovať ako:

-Komplexy: Roztoky sú vo forme z = p ± qi, kde p a q sú reálne čísla. Tento prípad zodpovedá prvému prípadu predchádzajúceho zoznamu.

-Čisté komplexy: Je to, keď sa skutočná časť roztoku rovná nule, to znamená, že riešenie má formu z = ± qi, kde q je skutočné číslo. Tento prípad zodpovedá prvému prípadu predchádzajúceho zoznamu.

-Komplexy s imaginárnou časťou rovnajúcou sa nule: Je to vtedy, keď sa komplexná časť roztoku rovná nule, to znamená, že riešenie je skutočné číslo. Tento prípad zodpovedá posledným dvom prípadom predchádzajúceho zoznamu.

Ako sa vypočítajú riešenia kvadratickej rovnice?

Na výpočet roztokov kvadratickej rovnice sa používa vzorec známy ako „rozlíšenie“, ktorý hovorí, že roztoky Ax²+BX+C = 0 sú dané vyjadrením nasledujúceho obrázka:

Suma, ktorá sa objaví v druhom druhom koreni, sa nazýva diskriminácia kvadratickej rovnice a je označená písmenom „D“.

Kvadratická rovnica bude mať:

-Dve skutočné riešenia áno, a iba áno, d> 0.

-Opakované skutočné riešenie, ak a iba v prípade, d = 0.

-Zero Real Solutions (alebo dve zložité riešenia) Áno a iba áno, D<0.

Príklady

-Riešenia rovnice x²+x-2 = 0 sú dané:

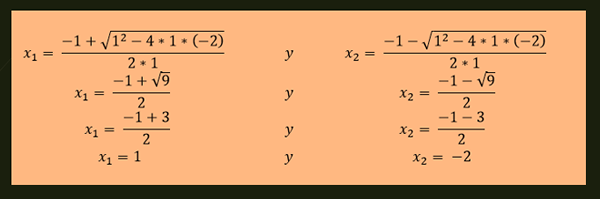
-Rovnica X²-4x+4 = 0 má opakované riešenie, ktoré je dané:

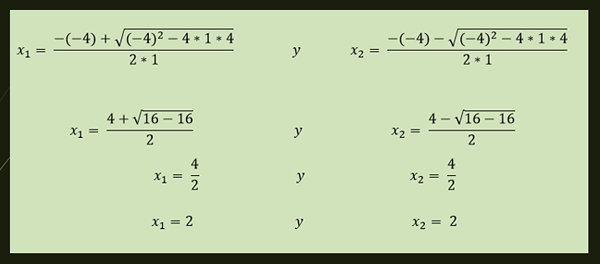
-Riešenia rovnice X²+1 = 0 sú uvedené:

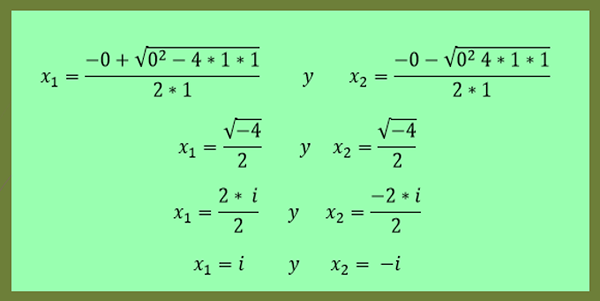
Ako je vidieť v tomto poslednom príklade, X2 je konjugát X1.