Valcové súradnice systém, zmeny a cvičenia

Ten valcové súradnice Slúžia na lokalizáciu bodov v trojrozmernom priestore a pozostávajú z radiálnej súradnice ρ, azimutálneho súradnice φ a súradnice výšky z.

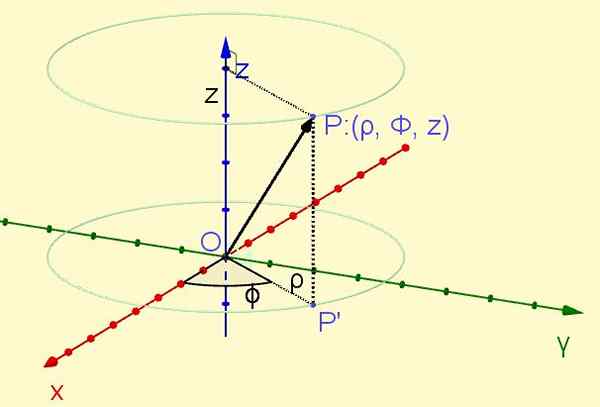
Bod P Nachádza sa vo vesmíre, premieta sa ortogonálne v lietadle Xy Vznik P ' V tomto lietadle. Vzdialenosť od pôvodu k bodu P ' definuje súradnicu ρ, zatiaľ čo uhol, ktorý tvorí os X S polotovarom Op ' Definujte súradnicu φ. Nakoniec súradnica z Je to ortogonálna projekcia bodu P na osi Z. (Pozri obrázok 1).

postava 1. Bod P valcových súradníc (ρ, φ, z). (Vlastné rozpracovanie)

Radiálna súradnica ρ je vždy pozitívna, azimutálna súradnica φ sa pohybuje od nulových radiánov po dva Radiany PI, zatiaľ čo súradnica Z môže mať akúkoľvek skutočnú hodnotu:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Zmena súradníc

Je relatívne jednoduché získať karteziánske súradnice (x, y, z) z bodu P z jeho valcových súradníc (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Je však tiež možné získať polárne súradnice (ρ, φ, z) na základe znalostí karteziánskych súradníc (x, y, z) bodu P:

ρ = √ (x² + a²)

φ = Arctan (y/x)

z = z

Vektorová báza vo valcových súradniciach

Je definovaná základňa valcových vektorov Uρ, Uφ, Uh.

Vektor Uρ Je dotyční k čiare φ = ctte a z = ctte (ukazuje radiálne von), vektor Uφ je dotyčnica k čiare ρ = ctte a z = ctte a nakoniec Uh Má rovnaký smer osi Z.

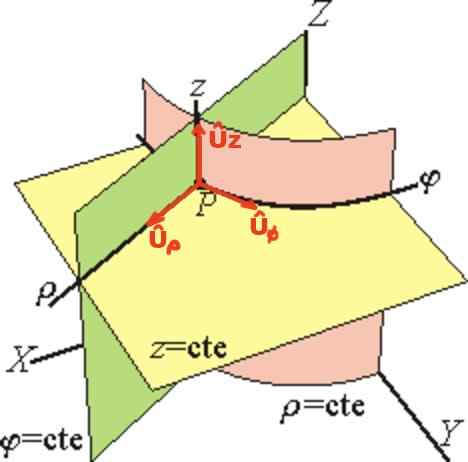Obrázok 2. Valcová súradnica. (Wikimedia Commons)

V základni valcovej jednotky je polohový vektor r Z bodu P je napísané vektorne takto:

Môže vám slúžiť: doména a rozpory funkcie (s príkladmi)

r = ρ Uρ + 0 Uφ + z Uh

Na druhej strane, nekonečné posunutie Dr Z bodu P je vyjadrený takto:

dr = Dρ Uρ + ρ dφ  Uφ + DZ Uh

Podobne aj nekonečný prvok objemu DV v valcových súradniciach je:

Dv = ρ dρ džen dz

Príklady

Existuje nespočet príkladov použitia a aplikácie valcových súradníc. Napríklad v kartografii valcová projekcia, založené presne na týchto súradniciach. Existuje viac príkladov:

Príklad 1

Valcové súradnice majú aplikácie v technológii. Ako príklad máte na pevnom disku, ktorý v skutočnosti pozostáva z niekoľkých diskov, systém CHS (sektor hlavy valca), ktorý v skutočnosti pozostáva z niekoľkých diskov:

- Valcový alebo stopa zodpovedá koordinácii ρ.

- Sektor zodpovedá polohe albumu φ, ktorá sa otáča na vysokej úrovni uhlová rýchlosť.

- Hlava zodpovedá polohe z čítacej hlavy na príslušnom albume.

Každý informačný bajt má presnú adresu vo valcových súradniciach (C, S, H).

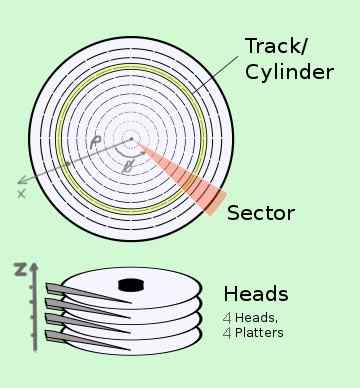Obrázok 2. Umiestnenie informácií vo valcových súradniciach v systéme pevný disk. (Wikimedia Commons)

Príklad 2

Stavebné žeriavy nastavili polohu zaťaženia vo valcových súradniciach. Horizontálna poloha je definovaná vzdialenosťou od osi žeriavu alebo šípkou. Vertikálna poloha zaťaženia je určená súradnicou Z výšky.

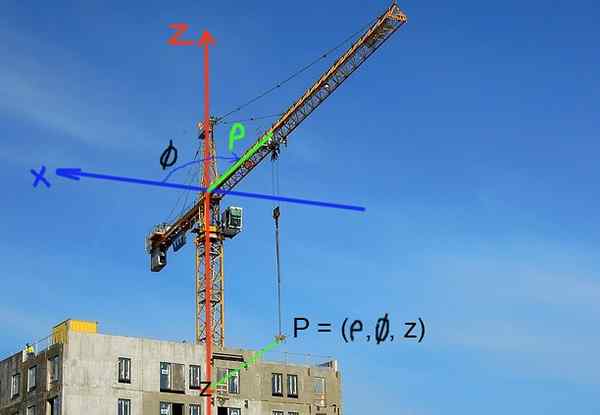Obrázok 3. Poloha zaťaženia v stavebnom žeriave sa dá ľahko vyjadriť vo valcových súradniciach. (Pixabay Image - RCOS R. Pérez)

Vyriešené cvičenia

Cvičenie 1

Existujú body P1 valcových súradníc (3, 120 °, -4) a bod P2 valcových súradníc (2, 90 °, 5). Nájsť Euklidovská vzdialenosť Medzi týmito dvoma bodmi.

Môže vám slúžiť: divízie, v ktorých je zvyšok 300

Riešenie: Najprv pokračujeme v nájdení karteziánskych súradníc každého bodu po vzorec, ktorý sa vyskytol vyššie.

P1 = (3* cos 120 °, 3* sen 120 °, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90 °, 2* sin 90 °, 5) = (0, 2, 5)

Euklidovská vzdialenosť medzi P1 a P2 je:

D (p1, p2) = √ ((0 - (-1.5))²+(2 - 2.60)²+(5 -(-4))² ) =…

… √ (2.25+0.36+81) = 9.14

Cvičenie 2

Bod P má karteziánske súradnice (-3, 4, 2). Nájdite zodpovedajúce valcovité súradnice.

Riešenie: Valcovité súradnice sa nachádzajú pomocou vyššie uvedených vzťahov:

ρ = √ (x² + a²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arktan (y/x) = arcan (4/(-3)) = -53.13 ° + 180 ° = 126.87 °

Z = 2

Malo by sa pamätať na to, že arcangentná funkcia je multitivaada periodicity 180 °. Okrem toho musí uhol φ patriť do druhého kvadrantu, pretože súradnice X E Y a bodových P sú v tomto kvadrante. To je dôvod, prečo bolo k výsledku pridané 180 °.

Cvičenie 3

Exprimujte vo valcových súradniciach a v karteziánskych koordinuje povrch rádiového valca 2 a ktorého os sa zhoduje s osou Z.

Riešenie: Rozumie sa, že valc má nekonečné predĺženie v smere Z, takže rovnica uvedeného povrchu vo valcových súradniciach je:

ρ = 2

Aby sa získala karteziánska rovnica valcového povrchu, štvorec oboch členov predchádzajúcej rovnice sa berie:

ρ² = 4

Vynásobíme 1 obom členmi predchádzajúcej rovnosti a uplatňujeme Základná trigonometrická identita (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

Zátvorka sa vyvíja na získanie:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Môže vám slúžiť: populácia a vzorka

Pamätáme si, že prvá zátvorka (ρ sen (φ)) je súradnica a bod v polárnych súradniciach, zatiaľ čo zátvorka (ρ cos (φ)) predstavuje súradnicu X, takže sme odišli Rovnica valca v karteziánskych súradniciach:

a² + X² = 2²

Predchádzajúca rovnica by sa nemala zamieňať s rockom kruhu v rovine XY, pretože v tomto prípade by to bolo také: a² + X² = 2² ; Z = 0.

Cvičenie 4

Polomerový valec r = 1 ma výška H = 1 m má svoju radiálne rozloženú hmotu podľa nasledujúcej rovnice D (ρ) = C (1 - ρ/r), kde C je konštanta hodnoty C = 1 kg/m³. Nájdite celkovú hmotnosť valca v kilogramoch.

Riešenie: Prvá vec je uvedomiť si, že funkcia D (ρ) predstavuje objemovú hustotu hmoty a že hmotnosť hustoty je distribuovaná v valcových kaskároch klesajúcej hustoty stredu do periférie. Infinitesimálny objemový prvok podľa symetrie problému je:

Dv = ρ dρ 2π h

Odtiaľ musíte, nekonečná hmotnosť valcovej škrupiny bude:

Dm = d (ρ) dv

Takže celková hmotnosť valca bude vyjadrená nasledujúcim Definovaný integrálny:

M = ∫_ani^R D (ρ) dv = ∫_ani^R C (1 - ρ/r) ρ dρ 2π H = 2π H C ∫_ani^R (1 - ρ/r) ρ dρ

Riešenie uvedeného integrálu nie je ťažké získať, pretože je jeho výsledkom:

∫_ani^R (1 - ρ/r) ρ dρ = (⅙) r²

Začlenenie tohto výsledku sa získa expresia hmotnosti valca:

M = 2π HC (⅙) r² = ⅓ π H c r² =

 ⅓ π 1m*1 kg/m³* 1 m² = π/3 kg ≈ 1.05 kg

Odkazy

1. Arfken G a Weber H. (2012). Matematické metódy pre fyzikov. Komplexný sprievodca. 7. vydanie. Akademická tlač. ISBN 978-0-12-384654-9
2. Výpočet. Riešené valcové a sférické problémy s koordináciou. Obnovené z: výpočtu.Dc
3. Weisstein, Eric W. „Valcovité súradnice.”Z Web Mathworld-A Wolfram. Obnovené z: Mathworld.Valfram.com
4. Wikipedia. Valcový súradnicový systém. Zdroj: In.Wikipedia.com
5. Wikipedia. Vektorové polia vo valcových a sférických súradniciach. Zdroj: In.Wikipedia.com