Integrácia konštantný význam, výpočet a príklady

Ten Konštanta Je to pridaná hodnota pri výpočte antideitív alebo integrálov, slúži na reprezentáciu riešení, ktoré tvoria primitívnosť funkcie. Vyjadruje inherentnú nejednoznačnosť, ak má nejaká funkcia nekonečný počet primitívnych.

Napríklad, ak je funkcia prijatá: F (x) = 2x + 1 a dostaneme jej antidevatívne:

∫ (2x+1) dx = x² + X + C ; Kde C Je to Konštanta a graficky predstavuje vertikálny preklad medzi nekonečnými možnosťami primitívneho. Je správne to povedať (x² + x) Je to a primitívneho f (x).

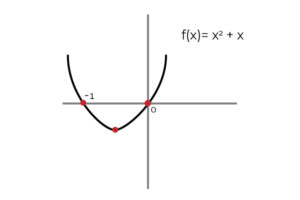Zdroj: autor

Rovnako môžete definovať (x² + X + C ) ako primitívny f (x).

[TOC]

Inverzná vlastnosť

Je možné poznamenať, že pri odvodení výrazu (x² + x) Získa sa funkcia f (x) = 2x + 1. Je to kvôli inverznej vlastnosti medzi odvodením a integráciou funkcií. Táto vlastnosť umožňuje získať integračné vzorce začínajúce od diferenciácie. Čo umožňuje overovanie integrálov prostredníctvom rovnakých derivátov.

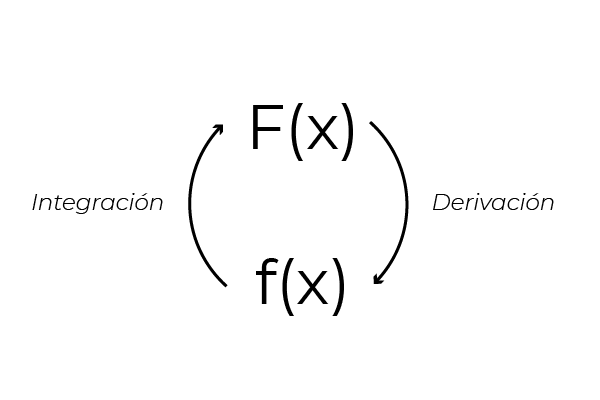Zdroj: autor

Avšak (x² + x) Nie je to jediná funkcia, ktorej derivát sa rovná (2x + 1).

1. D (X² + x)/ dx = 2x + 1
2. D (X² + x + 1)/ dx = 2x + 1
3. D (X² + x + 2)/ dx = 2x + 1
4. D (X² + x + 3)/ dx = 2x + 1
5. D (X² + X + C)/ dx = 2x + 1

Kde 1, 2, 3 a 4 predstavujú osobitný primitívny f (x) = 2x + 1. Zatiaľ čo 5 predstavuje neurčitú alebo primitívnu integrál F (x) = 2x + 1.

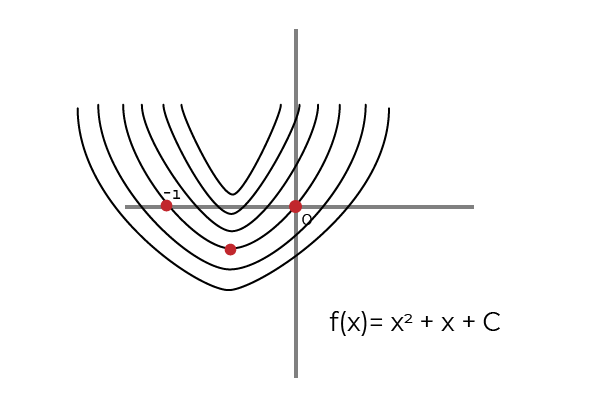Zdroj: autor

Primitívny funkcia sa dosahuje prostredníctvom antidevácie alebo integrálneho procesu. Kde f bude primitívny f, ak sa splní nasledujúce

• y = ∫ f (x) dx = F (x) + c; C = Konštanta
• F '(x) = f (x)

Oceňuje sa, že funkcia má jediný derivát, na rozdiel od jej nekonečného primitívneho výsledku v dôsledku integrácie.

Neurčitý integrál

 ∫ f (x) dx = f (x) + c

Zodpovedá rodine kriviek s rovnakým vzorom, ktorý zažíva nezrovnalosť v hodnote obrazov každého bodu (x, y). Každá funkcia, ktorá splní tento vzorec, bude individuálny primitívny a sada všetkých funkcií je známa ako Neurčitý integrál.

Hodnota Konštanta Bude to ten, ktorý diferencuje každú funkciu v praxi.

Ten Konštanta Navrhuje vertikálne posun vo všetkých grafoch, ktoré predstavujú primitívnu funkciu. Kde je medzi nimi pozorovaný paralelizmus a skutočnosť, že C Je to hodnota posunu.

Podľa bežných postupov Konštanta Po pridaní je označený písmenom „C“, hoci v praxi je ľahostajný, ak konštanta dodáva alebo odpočíta. Jeho skutočnú hodnotu možno nájsť rôznymi spôsobmi podľa rôznych počiatočné podmienky.

Ďalšie významy integračnej konštanty

Už sa hovorilo o tom, ako Konštanta sa uplatňuje v vetve integrálny počet; Predstavuje rodinu kriviek, ktoré definujú neurčitú integrál. Ale mnoho ďalších vied a pobočiek pridelilo veľmi zaujímavé a praktické hodnoty Konštanta, ktorí uľahčili vývoj viacerých štúdií.

Môže vám slúžiť: obdĺžnik Trapezoid: Vlastnosti, vzťahy a vzorce, príklady

V fyzický Integračná konštanta môže brať viac hodnôt podľa povahy údajov. Veľmi častým príkladom je poznať funkciu V (t) čo predstavuje rýchlosť častice verzus čas t. Je známe, že pri výpočte primitívneho V (t) sa získa funkcia R (t) čo predstavuje pozícia častíc verzus čas.

Ten Konštanta bude predstavovať hodnotu počiatočnej polohy, to znamená v okamihu t = 0.

Podobne, ak je funkcia známa A (t)  čo predstavuje zrýchlenie častíc verzus čas. Primitívny A (t) bude mať za následok funkciu V (t), kde Konštanta Bude to hodnota počiatočnej rýchlosti v₀.

V hospodárnosť, Získaním primitívneho funkcie nákladovej funkcie integráciou. Ten Konštanta bude predstavovať fixné náklady. A toľko ďalších aplikácií, ktoré si zaslúžia diferenciálny a integrálny počet.

Ako sa vypočíta integračná konštanta?

Pre výpočet Konštanta, Vždy bude potrebné poznať počiatočné podmienky. Ktoré sú zodpovedné za definovanie toho, ktorý z možných primitívnych je zodpovedajúci.

V mnohých aplikáciách sa považuje za nezávislú premennú času (t), kde konštanta C Vezmite hodnoty, ktoré definujú počiatočné podmienky konkrétny prípad.

Ak sa vezme počiatočný príklad: ∫ (2x+1) dx = x² + X + C

Platnou počiatočnou podmienkou môže byť podmienka grafiky na prejdenie špecifickej súradnice. Napríklad je známe, že primitívne (x² + X + C) Prejdite bodom (1, 2)

F (x) = x² + X + C; Toto je všeobecné riešenie

F (1) = 2

V tejto rovnosti nahrádzame všeobecné riešenie

F (1) = (1)² + (1) + C = 2

Kde sa to ľahko odvodí C = 0

Týmto spôsobom je zodpovedajúci primitívny pre tento prípad F (x) = x² + X

Existujú rôzne typy číselných cvičení, s ktorými pracujú Integrácia. V skutočnosti sa diferenciálny a integrálny počet neprestane uplatňovať pri súčasných vyšetrovaniach. Na rôznych akademických úrovniach nájdete; Od počiatočného výpočtu, prostredníctvom fyziky, chémie, biológie, hospodárstva,.

Oceňuje sa to aj v štúdiu diferenciálne rovnice, kde Konštanta Môžete brať rôzne hodnoty a riešenia, to je kvôli viacerým odporúčaniam a integráciám, ktoré sa vykonávajú v tejto veci.

Príklady

Príklad 1

1. Kanón umiestnený 30 metrov vysoký výhonky zvisle po projektil. Je známe, že počiatočná rýchlosť projektilu je 25 m/s. Určiť:

• Funkcia, ktorá definuje pozíciu projektilu vzhľadom na čas.
• Čas letu alebo čas, v ktorom sa častica hrá na zem.

Môže vám slúžiť: 8 typov chýb merania (s príkladmi)

Je známe, že v rovnomerne rozmanitom priamom zrýchlení pohybu je konštantná hodnota. Toto je prípad spustenia projektilu, kde bude zrýchlenie gravitáciou

G = - 10 m/s²

Je tiež známe, že zrýchlenie je druhým odvodeným z polohy, čo naznačuje dvojitú integráciu do rozlíšenia cvičenia, čím sa získa dva Integrácia.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

Počiatočné podmienky cvičenia naznačujú, že počiatočná rýchlosť je V₀ = 25 m/s. Toto je rýchlosť v čase času t = 0. Týmto spôsobom je splnené to:

V (0) = 25 = -10 (0) + C₁   a C₁ = 25

Definovaná funkcia rýchlosti

V (t) = -10t + 25; Môžete vidieť podobnosť s vzorcom MRUV (v_F = V₀ + X t)

V homológii je funkcia rýchlosti integrovaná na dosiahnutie výrazu, ktorý definuje pozíciu:

R (t) = ∫v (t) dt = ∫ (-10T+25) dt = -5t² + 25t + C₂

R (t) = -5t² + 25t + C₂  (Primitívna poloha)

Počiatočná poloha R (0) = 30 m je známa. Potom sa vypočíta konkrétny primitívny projektil.

R (0) = 30 m = -5 (0)² + 25 (0) + C₂ . Kde C₂ = 30

Prvá časť je odvtedy vyriešená R (t) = -5t² + 25T + 30  ; Táto expresia je homológna receptúry na vytesnenie v Mruv r (t) = r₀ + Vložka₀T - gt²/2

V druhej časti musí byť kvadratická rovnica vyriešená: -5t² + 25T + 30 = 0

Pretože podmienky častíc dosiahne zem (poloha = 0)

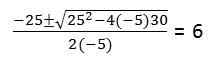Zdroj: autor

V skutočnosti rovnica 2. stupňa vyvoláva 2 riešenia t: 6, -1. Hodnota t = -1 sa ignoruje, pretože to sú jednotky času, ktorých doména neobsahuje záporné čísla.

Týmto spôsobom sa vyrieši druhá časť, v ktorej sa čas letu rovná 6 sekundám.

Príklad 2

2. Nájdite primitívny F (x), ktorý spĺňa počiatočné podmienky:

• f "(x) = 4; f '(2) = 2; f (0) = 7

S informáciami o druhom deriváte F "(x) = 4 Proces antidevácie sa začína

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Potom poznanie podmienky f '(2) = 2 pokračuje:

4 (2) + C₁ = 2

C₁ = -6 a f '(x) = 4x - 8

Postupovať rovnakým spôsobom pre druhý Konštanta

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Počiatočná podmienka f (0) = 7 je známa a pokračuje:

2 (0)² - 8 (0) + C₂ = 7

C₂ = 7 a f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Podobne ako v predchádzajúcom probléme definujeme prvé deriváty a pôvodnú funkciu z počiatočných podmienok.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + C₁

S podmienkou f '(0) = 6 pokračuje:

Môže vám slúžiť: Sada Teória: Charakteristiky, prvky, príklady, cvičenia

(0³/3) + C₁ = 6; Kde₁ = 6 a f '(x) = (x³/3) + 6

Potom druhý Konštanta

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Počiatočná podmienka f (0) = 3 je známa a pokračuje:

[(0)⁴/12] + 6 (0) + C₂ = 3; Kde₂ = 3

Získa sa konkrétny primitívny

f (x) = (X⁴/12) + 6x + 3

Príklad 3

3. Definujte primitívne funkcie vzhľadom na deriváty a bod grafu:

• dy/dx = 2x - 2, ktorý prechádza bodom (3, 2)

Je dôležité si uvedomiť, že deriváty sa vzťahujú na sklon čiary dotýkal krivky v určitom bode. Kde nie je správne predpokladať, že grafika derivátu sa dotýka uvedeného bodu, pretože patrí do grafu primitívnej funkcie.

Týmto spôsobom vyjadrujeme diferenciálnu rovnicu nasledovne:

dy = (2x - 2) dx  ; Potom pri uplatňovaní kritérií antidevácie máte:

∫dy = ∫ (2x - 2) dx

y = x² - 2x + c

Uplatňovanie počiatočnej podmienky:

2 = (3)² - 2 (3) + C

C = -1

Je získané: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1, ktorý prechádza bodom (0, 2)

Vyjadrujeme diferenciálnu rovnicu nasledovne:

dy = (3x² - 1) DX  ; Potom pri uplatňovaní kritérií antidevácie máte:

 ∫dy = ∫ (3x² - 1) DX

y = x³ - x + c

Uplatňovanie počiatočnej podmienky:

2 = (0)² - 2 (0) + c

C = 2

Je získané: f (x) = x³ - x + 2

Navrhované cvičenia

Cvičenie 1

1. Nájdite primitívny F (x), ktorý spĺňa počiatočné podmienky:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Cvičenie 2

2. Balón, ktorý stúpa rýchlosťou 16 stôp/s.

• Definujte čas letu
• Čo bude vektor V_F Keď sa dotknete podlahy?

Cvičenie 3

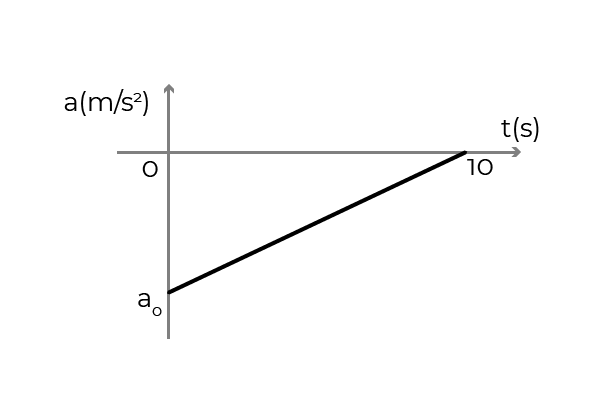
3. Obrázok zobrazuje graf zrýchlenia - čas automobilu, ktorý sa pohybuje v pozitívnom zmysle osi x. Auto cestovalo konštantnou rýchlosťou 54 km/h, keď vodič aplikoval brzdy na zastavenie za 10 sekúnd. Určiť:

• Počiatočné zrýchlenie vozidla
• Rýchlosť vozidla pri t = 5s
• Posunutie vozidla počas brzdenia

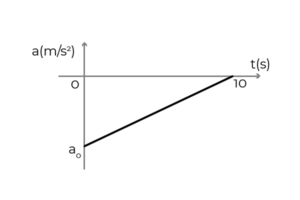Zdroj: autor

Cvičenie 4

4. Definujte primitívne funkcie vzhľadom na deriváty a bod grafu:

• dy/dx = x, ktorý prechádza bodom (-1, 4)
• dy/dx = -x² + 1, ktorý prechádza bodom (0, 0)
• dy/dx = -x + 1, ktorý prechádza bodom (-2, 2)

Odkazy

1. Integrálny počet. Integrálne integrálne a integračné metódy. Wilson, Velamsquez Bastidas. Univerzita Magdalena 2014
2. Stewart, J. (2001). Výpočet premennej. Skorý transcendentný. Mexiko: Thomson Learning.
3. Jiménez, r. (2011). Matematika VI. Integrálny počet. Mexiko: Pearson Education.
4. Fyzika i. MC Graw Hill