Matematika

Zhodné zhodné údaje, kritériá, príklady, cvičenia

Zhodné zhodné údaje, kritériá, príklady, cvičenia

Ten zhoda, V geometrii poukazuje na to, že ak majú dve ploché čísla rovnakú formu a rozmery, sú to zhodné. Napríklad dva segmenty sú zhodné, keď sú ich dĺžky rovnaké. Tiež zhodné uhly majú rovnaké opatrenie, aj keď nie sú v lietadle orientované rovnakým spôsobom.

Termín „zhoda“ pochádza z latinčiny Kongruencia, ktorého význam je korešpondencia. Takto dve zhodné čísla zodpovedajú presne jednou s druhou.

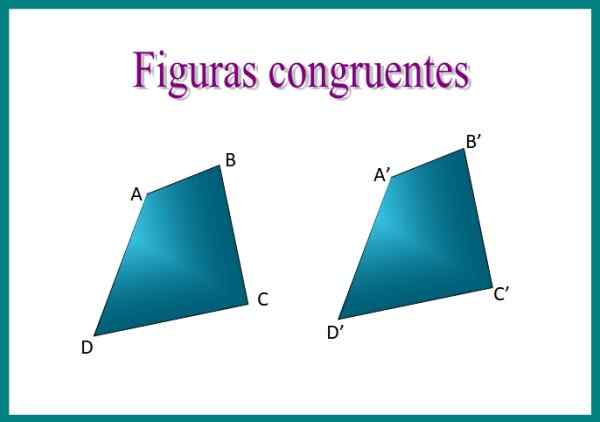
postava 1. Kvadrilaterály Abcd a A'b'c'd 'z obrázku sú zhodné: ich strany majú rovnaké opatrenie, ako aj ich vnútorné uhly. Zdroj: f. Zapata.

Napríklad, ak prekrývame dva kvadrilaterály obrazu, zistíme, že sú zhodné, pretože dispozícia ich strán je rovnaká a merajú to isté.

Pri umiestnení kvadrilaterálov Abcd a a'b'c'd 'na druhej. Zodpovedajúce strany sa volá homologické strany ani zodpovedajúci A na vyjadrenie zhody sa používa symbol ≡. Potom môžeme povedať, že abcd ≡ a'b'c'd '.

[TOC]

Zhodné kritériá

Pre zhodné polygóny sú spoločné nasledujúce charakteristiky:

-Rovnaký tvar a veľkosť.

-Rovnaké opatrenia vašich uhlov.

-Rovnaký rozsah na každej jeho stranách.

V prípade, že sú dva príslušné polygóny pravidelné, to znamená, že všetky strany a vnútorné uhly merajú to isté, zhoda je zaručená, keď je splnená jedna z nasledujúcich podmienok:

-Strany sú zhodné

-Ten apothémia mať rovnaké opatrenie

-On rozhlas každého polygónu meria rovnako

Apotheme pravidelného polygónu je vzdialenosť medzi stredom a jednou zo strán, zatiaľ čo polomer zodpovedá vzdialenosti medzi stredom a vrcholom alebo rohom obrázku.

Kritériá zhody sa často používajú, pretože mnoho častí a kusov všetkého druhu sa vyrába v sériách a musí mať rovnakú formu a opatrenia. Týmto spôsobom sa dajú ľahko vymeniť v prípade potreby, napríklad orechy, skrutky, plachty alebo dláždené zeme na ulici.

Môže vám slúžiť: Simpson Pravidlo: vzorec, demonštrácia, príklady, cvičeniaObrázok 2. Pouličné dláždené kamene sú zhodné postavy, pretože ich tvar a rozmery sú úplne rovnaké, hoci ich orientácia na podlahu sa môže zmeniť. Zdroj: Pixabay.

Zhoda, identita a podobnosť

Existujú napríklad geometrické koncepty týkajúce sa zhody Rovnaké čísla a podobné čísla, ktoré nevyhnutne neznamená, že čísla sú zhodné.

Všimnite si, že zhodné čísla sú identické, avšak švajtraky na obrázku 1 by sa mohli orientovať rôznymi spôsobmi v lietadle a stále sú naďalej zhodné, pretože iná orientácia nezmení veľkosť svojich strán alebo veľkosť ich uhlov. V tomto prípade by prestali byť rovnaké.

Druhou koncepciou je podobnosť obrázkov: dve ploché čísla sú podobné, ak majú rovnakú formu a ich vnútorné uhly sa merajú rovnako, hoci veľkosť obrázkov sa môže líšiť. Ak je to tak, čísla nie sú zhodné.

Príklady zhody

- Zhoda uhlov

Ako sme uviedli na začiatku, zhodné uhly majú rovnaké opatrenie. Existuje niekoľko spôsobov, ako získať zhodné uhly:

Príklad 1

Dva riadky so spoločným bodom definujú dva uhly, ktoré sa nazývajú Protichodné uhly podľa vrcholu. Tieto uhly majú rovnaké opatrenie, preto sú zhodné.

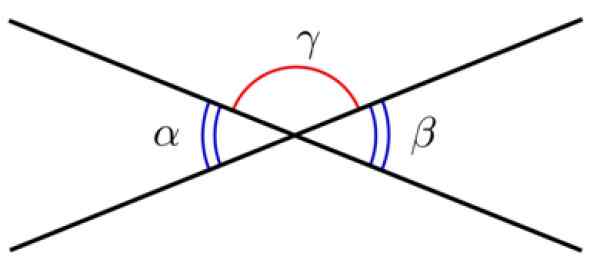Obrázok 3. Protichodné uhly podľa vrcholu. Zdroj: Wikimedia Commons.

Príklad 2

Existujú dve paralelné riadky plus čiara tón To ich pretína obaja. Rovnako ako v predchádzajúcom príklade, keď tento riadok pretína paralely, vytvára zhodné uhly, jeden na každej riadku na pravej strane a dva ďalšie na ľavej strane. Obrázok ukazuje a a a1, napravo od riadku tón, Sú zhodní.

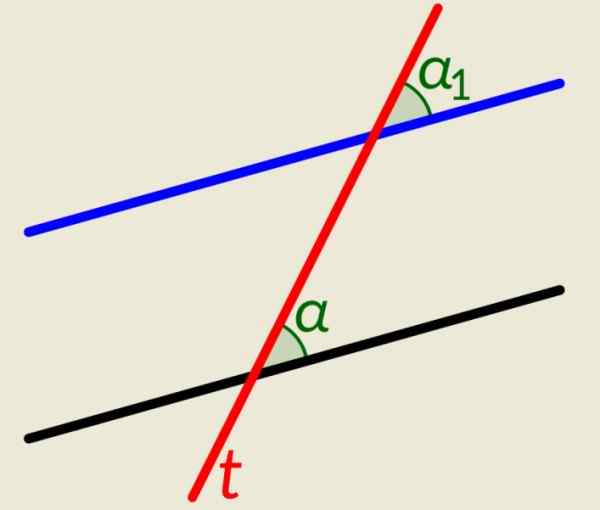Obrázok 4. Uhly zobrazené na obrázku sú zhodné. Zdroj: Wikimedia Commons. Lfahlberg/cc By-SA (https: // creativeCommons.Org/licencie/By-SA/3.0).

Príklad 3

V rovnobežníku sú štyri vnútorné uhly, ktoré sú zhodné dva až dva. Sú to tie medzi opačnými vrcholmi, ako je to znázornené na nasledujúcom obrázku, v ktorom sú dva zelené uhly zhodné, ako aj dva uhly v červenej farbe.

Môže vám slúžiť: acutangle trojuholník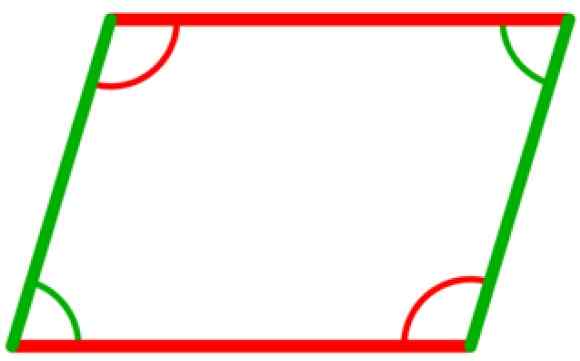Obrázok 5. Vnútorné uhly rovnobežníka sú zhodné dva až dva. Zdroj: Wikimedia Commons.

- Zhoda trojuholníkov

Dva trojuholníky identického tvaru a rovnakej veľkosti sú zhodné. Aby sme to overili, existujú tri kritériá, ktoré je možné preskúmať pri hľadaní zhody:

-Kritériá LLL: Tri strany trojuholníkov majú rovnaké opatrenia, preto l1 = L '1; L2 = L '2 a l3 = L '3.

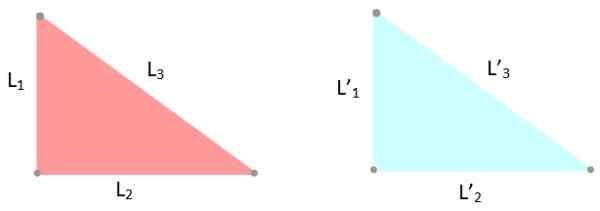Obrázok 6. Príklad zhodných trojuholníkov, ktorých strany merajú rovnako. Zdroj: f. Zapata.

-Kritériá aal: Triangly majú dva rovnaké vnútorné uhly a strana medzi týmito uhlami má rovnaké opatrenie.

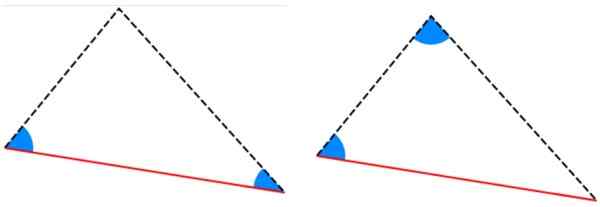Obrázok 7. Kritériá ala a aal pre zhodu trojuholníkov. Zdroj: Wikimedia Commons.

-Kritérium: Dve strany sú identické (zodpovedajúce) a medzi nimi je rovnaký uhol.

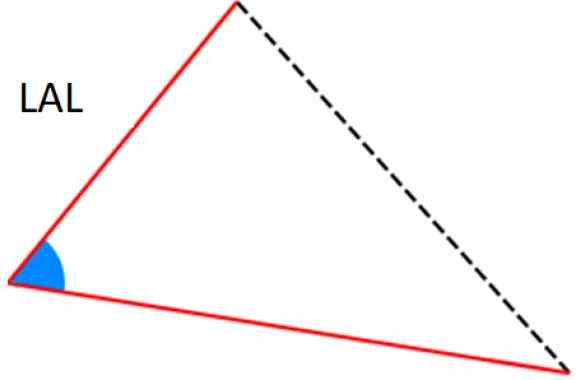Obrázok 8. LAL Kritériá pre zhodu trojuholníkov. Zdroj: Wikimedia Commons.

Vyriešené cvičenia

- Cvičenie 1

Na obrázku sú znázornené dva trojuholníky: AABC a AECF. Je známe, že ac = ef, že ab = 6 a že cf = 10. Okrem toho sú uhly ∡bac a ∡fec zhodné a uhly ∡acb a ∡FCB sú tiež.

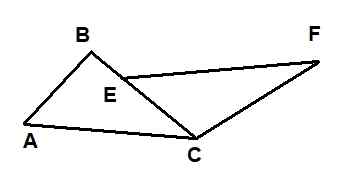Obrázok 9. Trojuholníky pre príklad vyriešené 1. Zdroj: f. Zapata.

Potom sa dĺžka segmentu BE rovná:

i) 5 

Ii) 3

Iii) 4 

(Iv) 2

v) 6

Riešenie

Pretože dva trojuholníky majú jednu stranu rovnakej dĺžky AC = EF medzi rovnakými uhlami ∡bac = ∡Cef a ∡BCA = ∡CFE sa dá povedať, že dva trojuholníky sú zhodné podľa krídla kritérií.

To je ΔBAC ≡ ΔCEF, takže musíte:

BA = CE = AB = 6

Bc = cf = 10

AC = EF

Ale segment, ktorý chcete vypočítať, je BE = BC - EC = 10 - 6 = 4.

Takže správnou odpoveďou je (iii).

- Cvičenie 2

Na obrázku sú znázornené tri trojuholníky. Je tiež známe, že dva označené uhly merajú každý 80 ° a že segmenty AB = PD a AP = CD. Nájdite hodnotu uhla x uvedeného na obrázku.

Môže vám slúžiť: polybal grafika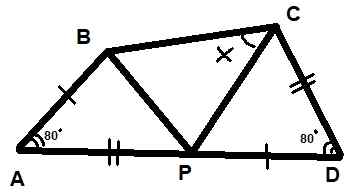Obrázok 10. Trojuholníky pre príklad vyriešené 2. Zdroj: f. Zapata.

Riešenie

Musíte aplikovať vlastnosti trojuholníkov, ktoré sú podrobne krok za krokom.

Krok 1

Počnúc kritériami zhody Lal trojuholníkov je možné povedať, že trojuholníky BAP a PDC sú zhodné:

Δbap ≡ Δpdc

Krok 2

Vyššie uvedené vedie k potvrdeniu, že BP = PC, preto trojuholník ABPC je izoscely a ∡pcb = ∡pbc = x.

Krok 3

Ak zavoláme γ v uhle BPC, nasleduje to:

2x + γ = 180 °

Krok 4

A ak zavoláme β k uhlom APB a DCP a a do uhlov ABP a DPC, musí:

a + β + γ = 180 ° (pretože APB je plochý uhol).

Krok 5

Okrem toho a + β + 80 ° = 180 ° podľa súčtu vnútorných uhlov trojuholníka APB.

Krok 6

Kombinácia všetkých týchto výrazov musíte:

a + β = 100 °

Krok 7

A preto:

γ = 80 °.

Krok 8

Nakoniec to nasleduje:

2x + 80 ° = 180 °

S x = 50 °.

Odkazy

  1. Baldor, a. 1973.Geometria plochej a vesmíru. Stredoamerický kultúrny.
  2. Nadácia CK-12. Zhodné polygóny. Zdroj: CK 12.orgán.
  3. Užite si matematiku. Definície: Rádio (polygón). Získané z: Vychutnajte si.com.
  4. Matematika otvorená referencia. Testovanie polygónov na zhodu. Získané z: Mathpenref.com.
  5. Wikipedia. Zhoda (geometria). Obnovené z: je.Wikipedia.orgán.
  6. Zapata, f. Trojuholníky, história, prvky, klasifikácia, vlastnosti. Zdroj: Lifer.com.