Koncepcia konceptu

On reštitúcia Je to kvocient medzi relatívnou rýchlosťou prekročenia rýchlosti a relatívnou rýchlosťou priblíženia k dvom telám, ktoré sa zrážajú. Ak sú telá zjednotené po zrážke, tento kvocient je neplatný. A jednotka stojí za to, aby bola kolízia úplne elastická.

Predpokladajme, že dve solídne sféry hmoty M1 a hmotnosť M2 To, že trpia kolíziou. Tesne pred kolíziou mali gule rýchlosti V1 a V2 Pokiaľ ide o určitý inerciálny referenčný systém. Hneď po zrážaní ich rýchlosti sa menia na V1 ' a V2 '.

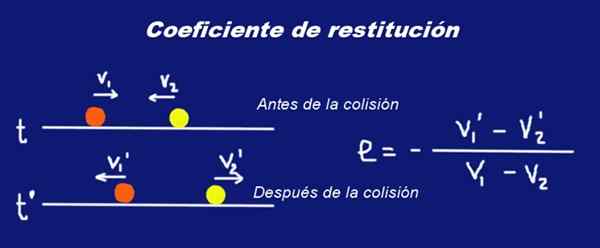postava 1. Kolízia dvoch guľôčok Mases M1 a M2 a ich koeficient reštitúcie a. Pripravil Ricardo Pérez.

Bol umiestnený odvážne písmo V rýchlostiach, ktoré naznačujú, že ide o vektorové množstvá.

Experimenty naznačujú, že každá zrážka spĺňa nasledujúci vzťah:

V1 ' - V2 '= -a (V1 - V2)

Kde a Je to skutočné číslo medzi 0 a 1, nazývané reštitúcia kolízia. Predchádzajúci výraz sa interpretuje takto: 

Relatívna rýchlosť dvoch častíc pred kolíziou je úmerná relatívnej rýchlosti týchto dvoch častíc po zrážke, konštanta proporcionality je (-e), kde E je koeficient reštitúcie kolízie.

[TOC]

Aký je koeficient reštitúcie pre?

Užitočnosť tohto koeficientu spočíva v poznaní stupeň neelasticity zrážky. V prípade, že je kolízia dokonale elastická, koeficient bude 1, zatiaľ čo v úplne nepružnej kolízii bude koeficient hodnotiť 0, pretože v tomto prípade je relatívna rýchlosť po zrážke nulová.

Recipročne, ak sú pred ním známe restitučný koeficient kolízie a rýchlosti častíc, potom sa dá predpovedať rýchlosť po takejto zrážke. 

Môže vám slúžiť: 13 príkladov Newtonovho prvého zákona v reálnom živote

Hybnosť

Pri zrážkach, okrem vzťahu, ktorý ustanovil koeficient reštitúcie, existuje aj ďalší základný vzťah, ktorý je Ochrana hybnosti.

Hybnosť p častíc alebo množstva pohybu, ako sa nazýva, je produktom hmotnosti M častice pre svoju rýchlosť Vložka. To je: hybnosť p Je to vektorová suma.

V zrážkach lineárna hybnosť P Systém je rovnaký tesne pred a hneď po zrážke, pretože vonkajšia sila je opovrhnutia proti krátkym, ale intenzívnym silám vnútornej interakcie počas kolízie. Ale zachovanie hybnosti nestačí P systému na riešenie všeobecného problému kolízie.

V predtým uvedenom prípade je zrážacie dve gule M1 a M2, ochrana lineárnej hybnosti je napísaná takto:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Neexistuje spôsob, ako vyriešiť problém s kolíziou, ak nie je známy koeficient reštitúcie. Ochrana hybnosti, aj keď je to potrebné, nie je dostatočná na predpovedanie rýchlosti po zrážke.

Keď problém uvádza, že telá sa po zrážke pohybujú spolu, implicitne hovorí, že koeficient reštitúcie je 0.

Obrázok 2. V biliardových loptičkách existujú zrážky koeficientu reštitúcie o niečo menej ako 1. Zdroj: Pixabay.

Koeficient energie a reštitúcie 

Ďalším dôležitým fyzickým množstvom zapojeným do zrážok je energia. Počas kolízií existujú výmeny kinetickej energie, potenciálnej energie a iných druhov energie, ako je kalorická energia.

Pred a po zrážke je potenciálna energia interakcie prakticky nulová, takže energetická bilancia zahŕňa kinetickú energiu častíc pred a po a po množstve Otázka nazývaná rozptýlená energia.

Môže vám slúžiť: Heisenberg Atomic Model

Pre dve gule M1 a M2, ktoré zrážajú energetickú rovnováhu pred a po zrážke, je napísaná takto:

½ M1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + q

Keď sú interakčné sily počas kolízie čisto konzervatívne, stáva sa to, že Celková kinetická energia Z častíc, ktoré sa zrážajú, to znamená, že je to isté pred a po zrážke (q = 0). Ak k tomu dôjde, hovorí sa, že kolízia je úplne elastická.

V prípade elastických zrážok sa energia nerozptyľuje. A tiež koeficient reštitúcie vyhovuje: E = 1. 

Naopak, v nepružných zrážkach, ktoré ≠ 0 a 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Aby bol problém s kolíziou dokonale určený, je potrebné poznať koeficient reštitúcie alebo striedavo množstvo energie rozptýlenej počas zrážky.

Koeficient reštitúcie závisí od povahy a typu interakcie medzi týmito dvoma telami počas kolízie.

Na druhej strane, relatívna rýchlosť telies pred kolíziou definuje intenzitu interakcie, a teda jej vplyv na koeficient reštitúcie. 

Ako sa vypočíta koeficient reštitúcie?

Na ilustráciu, ako sa vypočíta koeficient restitúcie kolízie, budeme mať jednoduchý prípad:

Predpokladajme, že kolízia dvoch hmotnostných sfér M1 = 1 kg a M2 = 2 kg ktoré sa pohybujú po priamom trení (ako na obrázku 1).

Prvá guľa ovplyvňuje počiatočnú rýchlosť V1 = 1 m/s Asi druhý, ktorý je pôvodne v pokoji, to znamená V2 = 0 m/s.

Môže vám slúžiť: Prvý zákon termodynamiky: vzorce, rovnice, príklady

Po zrážke sa pohybujú takto: prvý sa zastaví (V1 '= 0 m/s) a druhý sa pohybuje doprava s rýchlosťou V2 '= 1/2 m/s.

Na výpočet koeficientu reštitúcie v tejto zrážke uplatňujeme vzťah:

V1 ' - V2 ' = -a ( V1 - V2 ) 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Príklad

Pri jednej rozmerovej kolízii dvoch sfér predchádzajúcej sekcie sa vypočítal jej koeficient restution, čo viedlo k E = ½ .

Pretože E ≠ 1 kolízia nie je pružná, to znamená, že kinetická energia systému sa nezachováva a existuje určité množstvo rozptýlenej energie Q (napríklad zahrievanie guľôčok kvôli kolízii).

Určte hodnotu energie rozptýlenej v jouloch. Vypočítajte tiež percentuálnu frakciu rozptýlenej energie.

Riešenie

Počiatočná kinetická energia gule 1 je: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Zatiaľ čo v Sphere 2 je nula na to, aby ste boli spočiatku v pokoji.

Takže počiatočná kinetická energia systému je ki = ½ j.

Po zrážke sa iba druhá guľa pohybuje rýchlosťou v2 '= ½ m/s, takže konečná kinetická energia systému bude:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j

To znamená, že energia rozptýlená pri zrážke je:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

A zlomok energie rozptýlenej pri tejto zrážke sa vypočíta takto:

F = q / ki = ¼ / ½ = 0,5, to znamená, že 50% systémovej energie bolo rozptýlených z dôvodu nepružnej zrážky, ktorej koeficient reštitúcie je 0,5.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. 2005. Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
3. Rytier, r. 2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
4. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.
5. Wikipedia. Pohyb.Obnovené z: je.Wikipedia.orgán.