Sa volá Významné čísla na množstvo číslic, ktoré obsahujú Mantisa číslo. Čím viac čísel je množstvo známe s najväčšou presnosťou. Pripomíname, že Mantisa je postava, ktorá sprevádza silu 10, keď je napísané číslo vo vedeckom zápise.

Napríklad vezmeme číslo 0.00376, ktorý je napísaný ako 3.76 x 10 ^-3. Mantisa je 3.76 a počet má celkom 3 významné údaje. Číslo 0.129 má tiež 3 významné čísla, zatiaľ čo 4.5 má iba 2.

postava 1. Vedecké kalkulačky nikdy nezobrazujú počet významných údajov o operácii. Zdroj: piqsels.

A čo sa stane, keď je číslo celé? To znamená, že je známy s všetkou možnou presnosťou, inými slovami, má nekonečnú presnosť. Napríklad tým, že počítam ľudí, zvierat alebo predmety, ako sú knihy a telefóny, výsledkom je celé číslo a presné číslo.

Ak povieme, že v kine je 110 ľudí, ktorí sledujú film, je to presný počet, ani viac, ani menej a má 3 významné čísla.

Významné údaje sa zaoberajú niektorými jednoduchými pravidlami, ktoré sa zapamätajú s trochou praxe, ako uvidíme potom.

[TOC]

Pravidlá na určenie významných čísel čísla

Pravidlo 1

Predchádzajúce nuly sa nepovažujú za významnú hodnotu, takže 0.045 a 4.5 Majú obe 2 významné čísla, pretože tieto sa začínajú počítať zľava a od prvej inej číslice nuly.

Pravidlo 2

Zadné nuly (napravo) k prvej významnej číslici sa počítajú ako významná hodnota (pokiaľ je odôvodnená presnosťou meracieho prístroja).

Nakoniec, nuly, ktoré sú v strede, sa tiež považujú za významnú číslicu.

Pravidlo 3

Pre čísla napísané vo vedeckom zápise sú všetky čísla Mantisa významné a exponent neovplyvňuje presnosť.

Môže vám slúžiť: Priemerná rýchlosť: vzorce, ako sa vypočítava a vyrieši

Pravidlo 4

Ak sa vykonávajú operácie s desatinníkmi, napríklad výpočtom oblastí alebo iných podobných operácií, výsledok musí mať rovnaký počet významných údajov ako suma s najnižším počtom významných údajov, ktoré sa zúčastnili na operácii. Toto pravidlo je platné pre každú aritmetickú operáciu.

Pravidlo 5

Počet čísla neovplyvňuje jeho počet významných čísel.

Okamžite uvidíme niekoľko príkladov toho a všetky ostatné pravidlá.

Príklady

Príklad 1

Zistite, koľko významných čísel je v každom z týchto čísel.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Odpovedať

a) 876 má 3 významné čísla.

b) 1000.68 má 6 významných čísel, pretože nuly v strednom počte ako také.

c) Namiesto toho 0.00005026 má 4 významné čísla. Všimnite si, že 5 nulov vľavo od 5 sa nepočíta ako významná hodnota, namiesto toho na 0 medzi 5 a 2 áno.

d) 4.8 má 2 významné čísla.

e) -6.99 má 3 významné čísla.

Príklad 2

Je bežné prijať opatrenia, ako sú metrické pásky, hodinky, teplomery, váhy atď. Koľko významných údajov by sme mali nahlásiť sumy, ktoré týmto spôsobom merajú?

Odpoveď

Závisí to od ocenenia nástroja, s ktorým sa meria. Uveďme príklad: Zmerajte vonkajší priemer trubice, s absolvovaným pravidlom a s Vernier alebo King's Foot.

Vernier je nástroj, ktorý meria dĺžky veľmi presne preto vernier, čo umožňuje pri meraní väčšiu jemnosť.

Je to presnejšie ako absolventované pravidlo, pretože s ním sa môžeme dozvedieť významnejšie čísla určitej dĺžky.

Preto nemá zmysel nahlásiť obvod, povedzme, 35.88 cm Ak to zmeráme pomocou pásky, pretože tento nástroj nie je dosť presný na to, aby hlásil toľko významných číslic.

Môže vám slúžiť: statická: história, aké štúdie, aplikácie, zákony

Ocenenie A merania pásky je uvedené:

Pre kazetu alebo pravidlo milimetra, A = 1 mm, čo je desatina centimetra. Obvod meraný meracou páskou musí byť uvedený ako 35.9 cm.

Príklad 3

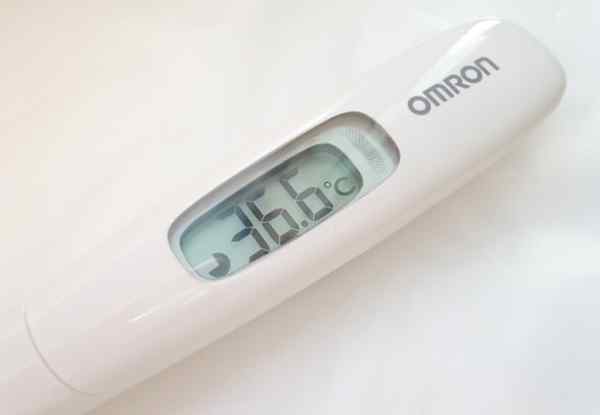
Koľko významných čísel má čítanie s digitálnym teplomerom?

Odpoveď

Teplomer na obrázku ponúka hodnoty teploty s tromi číslicami. Avšak v uvedenom rozsahu, 36.6 ° C, presné sú iba prvé dve číslice zľava doprava, pretože desatinné miesto je ovplyvnené chybou ocenenia nástroja, ktorý je zvyčajne uvedený v zadnej časti toho istého alebo v jeho prevádzkovej príručke.

Zvyčajná vec pre typ zobrazeného digitálneho nástroja je chyba 0 ocenenia.1 ° C. To stačí na to, aby ste si boli istí, že neexistuje horúčka.

Obrázok 2. Digitálny teplomer, ktorého hodnoty sú 3 významné čísla. Zdroj: pxhere.

Pravidlá na zaokrúhlenie čísel

Ak sa kalkulačka používa na vykonanie výpočtov s získanými opatreniami, nie je správne poskytnúť výsledok pomocou všetkých číslic, ktoré sa zobrazujú na obrazovke.

Iba tí, ktorí sa navzájom poznajú presne, sa zachovávajú, pretože iba tí majú skutočný význam. Potom je potrebné zaokrúhliť výsledky, aby sa prispôsobil presnému počtu čísel známych. Tieto pravidlá sú:

-Ak je číslo, ktoré nasleduje po zadržaní číslice rovná sa alebo je viac ako 5, K tejto číslici sa pridá 1.

Napríklad zaokrúhľovaním 3.786 Ak chcete mať dve desatinné miesta, chceme si udržať čísla až do 8. Pretože nasledujúce číslo (6) je väčšie ako 5, 8 sa stáva 8 + 1 = 9 a číslo zostáva 3.79.

-Keď je číslo nasledujúce po zadržaní číslice Menej ako 5, Číslica je rovnaká.

Môže vám slúžiť: Joule Effect: Vysvetlenie, príklady, cvičenia, aplikácie

Ak chceme 1. kolo.27924 mať iba 3 desatinné miesta, čo sa dosiahne dosiahnutím 9, po ktorom nasleduje 2. Pretože 2 je menšie ako 5, tieto desatinné miesta zmiznú a zaokrúhlené číslo je 1.279.

Cvičenie

Jedáleň má tvar a rozmery uvedené na pripevnenej postave. Žiada sa o výpočet svojej oblasti pomocou pravidiel operácií s významnými údajmi.

Riešenie

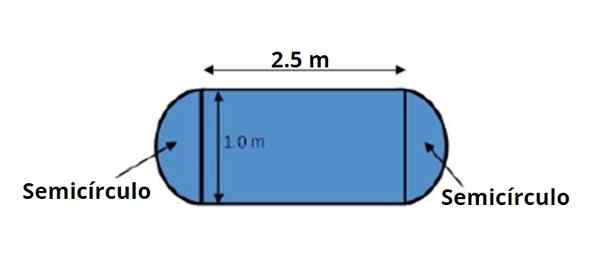Obrázok 3. Tabuľka obsahuje tvar a rozmery uvedené na obrázku, všimnite si, že sú známe s dvoma významnými číslami. Zdroj: f. Zapata.

Oblasť tabuľky sa dá rozdeliť do centrálnej obdĺžnikovej oblasti a dvoch polkruhov, jedna na každej strane, ktorá spolu vytvára 1 celý kruh.

Zavoláme₁ do oblasti obdĺžnika, dané:

Do₁ = báza × výška = 2.5 m x 1.0 m = 2.5 m²

Pokiaľ ide o oblasť kruhu, ktorá je rovnocenná s objemom 1 polkruhu vynásobený 2, je:

Do₂ = π × rádio²

Priemer ktoréhokoľvek z polovodičov je 1.0 m, preto polomer je 0.50 m. Priemer by sa mohol použiť priamo na výpočet oblasti v tomto prípade:

Do₂ = (π × priemer²) / 4

V každom prípade:

Do₂ = [π x (1.0 m)²] / 4 = 0.785398163 M²

Boli použité všetky číslice ponúkané kalkulačkou. Teraz pridávame do₁ už₂ Pre celkovú plochu tabuľky:

A = (2.5 + 0.785398163) M² = 3.285398163 M²

Pretože rozmery tabuľky sú známe s 2 významnými číslami, nemá zmysel vyjadriť výsledok so všetkými desatinnými číslami danými kalkulačkou, ktorá nikdy neposkytuje počet významných čísel výsledku.

Je potrebné urobiť to, aby ste obiehli oblasť tak, aby mala rovnaký počet významných čísel ako rozmery tabuľky, tj 2. Preto sa hlási konečný výsledok takto:

A = 3.3 m²

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 1. Kinematika. Editoval Douglas Figueroa (USB).
3. Fisicalab. Významné čísla a zaokrúhlenie. Získané z: Fisicalab.com.
4. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Objem1.